Контрольные вопросы и задания

1. Что такое звук? Каков диапазон частот звуковых волн? От чего зависит скорость звука?

2. Может ли звук распространяться в вакууме? Ответ обоснуйте.

3. Запишите уравнение бегущей волны и поясните величины, входящие в уравнение.

4. Дайте определение стоячей волны. Как возникают стоячие волны?

5. Выведите уравнение стоячей волны.

6. Что такое узлы и пучности? Получите уравнения координат узлов и пучностей.

7. В чем отличие стоячей волны от бегущей?

8. Построить график стоячей волны для фиксированного момента времени t = 0, T/8, T/4, 3T/8 или T/2 (или для других моментов по указанию преподавателя).

9. Обоснуйте расчетную формулу для скорости звука.

10. Опишите экспериментальную установку и методику определения скорости звука.

Литература

1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.

2. Детлаф А. А. , Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.

3. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970

4. Лабораторный практикум по физике: Учеб. пособие для студентов втузов./ Ахматов А.С., Андреевский В.М., Кулаков А.И. и др.; Под редакцией А.С. Ахматова. – М.: Высшая школа. 1980. – 360 с.

Часть III. Молекулярная физика, термодинамика, явления переноса

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ

ПО МЕТОДУ КЛЕМАНА И ДЕЗОРМА

Цель работы – определить отношение теплоемкостей для воздуха.

Приборы и принадлежности – стеклянный баллон емкостью около 25 литров с краном, манометр, насос, соединительные трубки.

Теоретическое введение

Удельной теплоемкостью вещества называется физическая величина, равная количеству теплоты, необходимой для нагревания единицы массы вещества на 1 ^оС(К) в данном процессе.

Молярной теплоемкостью вещества называется физическая величина, равная количеству теплоты, необходимой для нагревания одного моля вещества на 1^оС(К) в данном процессе.

Очевидно,

где молярная масса вещества.

Для газов принято различать теплоемкость при постоянном объеме С_v и при постоянном давлении C_p, в зависимости от процесса нагревания газа.

Согласно первому закону термодинамики количество переданной системе теплоты расходуется на увеличение внутренней энергии системы и работу расширения

dQ=dU+dA

При нагревании газа при V=const работа расширения dA=0, и все тепло идет на увеличение внутренней энергии, т.е. на нагревание газа.

При нагревании газа при P=const тепло затрачивается не только на нагревание, но и на работу расширения газа. Поэтому С_p > С_v.

Согласно кинетической теории идеального газа

где z – число степеней свободы молекулы

n – число молей газа

T –температура по шкале Кельвина

R – универсальная газовая постоянная

Соответственно: для двухатомного газа z = 5 и γ = 1,40; для многоатомного z = 6 и γ = 1,33.

Для экспериментального определения воздуха в данной работе используется адиабатический процесс расширения или сжатия.

Адиабатическим процессом называется процесс без теплового обмена с окружающей средой. dQ=0

Первое начало термодинамики для адиабатического процесса запишется как

0=dU+dA

или

а) dU = – dA - увеличение внутренней энергии газа (нагревание) происходит за счет работы внешних сил, совершающих сжатие газа.

б) dA = – dU – работа расширения, совершаемая газом, происходит за счет уменьшения его внутренней энергии.

Таким образом, при адиабатическом сжатии газ нагревается, при адиабатическом расширении – охлаждается.

Для осуществления адиабатического процесса нужно либо теплоизолировать систему, либо вести процесс так быстро, чтобы теплообмен не успел произойти.

Описание установки.

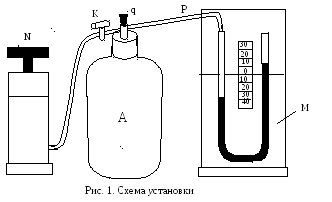
Стеклянный баллон А емкостью 25 литров с пробкой q соединен резиновыми трубками с насосом N и манометром М. На трубке, соединяющей баллон с насосом, имеется кран К (см. рис. 1).

Проведение эксперимента

I. Определение при сжатии воздуха.

1) Перед опытом открыть пробку q. Давление воздуха в баллоне А станет равным атмосферному давлению, и жидкость в манометре установится на одном и том же уровне в обоих коленах.

2) Закрыть трубку сосуда пробкой q, открыть кран К и осторожно накачать при помощи насоса N некоторое количество воздуха. Уровень жидкости в левом (соединенном с баллоном) колене начинает при этом опускаться, а в правом – подниматься.

Накачивать воздух следует до тех пор, пока разность высот уровней жидкости в манометре не достигнет нескольких десятков сантиметров ( 25 – 30 см ). (При накачивании воздух в баллоне сжимается, и температура его повышается ).

3) Закрыть кран К и дать воздуху в баллоне охладиться до комнатной температуры. Так как при охлаждении газа в баллоне его давление понижается, то разность уровней жидкости в манометре несколько уменьшается. Когда температура в баллоне станет равной температуре окружающего воздуха, перемещение уровней жидкости в манометре прекратится, и установится определенная разность высот h₁ , которую отмечают по шкале манометра. Давление внутри баллона будет равно

P_{1 =} H + h₁ ,

где Н – атмосферное давление. Удельный объем газа (объем, занимаемый единицей массы газа) в баллоне будет V₁, а температура t₁ = t_{комн .} Это состояние изобразится точкой А на графике, приведенном в таблице 1.

4). Открыть и очень быстро закрыть пробку q . При этом с воздухом в баллоне произойдут два следующие друг за другом процесса:

а). В момент открытия пробки происходит быстрое расширение воздуха, заключенного в баллоне, которое можно считать адиабатическим из-за его кратковременности. Давление при этом упадет до атмосферного и будет равно Р₂ = Н объем возрастает до V₂ , так как часть воздуха вышла, и на единицу массы теперь приходится больший объем. Температура становится ниже комнатной t₂ < t₁ , так как воздух адиабатически расширился. Это второе состояние изображается на графике, приведенном в таблице 1, точкой В.

б). После закрытия пробки q через 2 – 3 минуты воздух в баллоне в результате теплообмена снова нагревается до комнатной температуры t_к . В процессе теплообмена происходит изохорическое нагревание воздуха, так как удельный объем V₂ остается неизменным. При этом давление воздуха возрастает до

Р_{3 =}Н + h₂.

Разность уровней h₂ ( после того, как она установится ) снова отмечают по шкале манометра. Это третье состояние газа изобразится точкой С (см. тот же график и таблицу).

Состояниям А и С соответствует одна и та же температура, поэтому на графике эти точки можно соединить изотермой.

Таблица трех состояний в процессе работы не заполняется, она нужна для вывода расчетной формулы.

Таблица 1

Три состояния воздуха при сжатии и графики соответствующих переходов

При каких условиях	Состоя- ние	Уд. объем	Давле- ние	Темпе- ратура	V V
До откры- тия пробки	А	V1	H +h1	tк
В момент открытия пробки	В	V2	H	t2
После закрытия пробки	С	V2	H + h2	tк

Таблица 2

Три состояния воздуха при расширении и графики соответствующих переходов

При каких условиях	Состоя- ние	Уд. объем	Давле- ние	Темпе- ратура
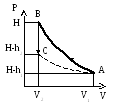
До откры- тия пробки	А	V1	H – h1	tк
В момент открытия пробки	В	V2	H	tк
После закрытия пробки	С	V2	H – h2	tк

Вывод расчетной формулы

Рассматривая переход воздуха из состояния А в состояние В как процесс адиабатический, применим к нему уравнение Пуассона

или 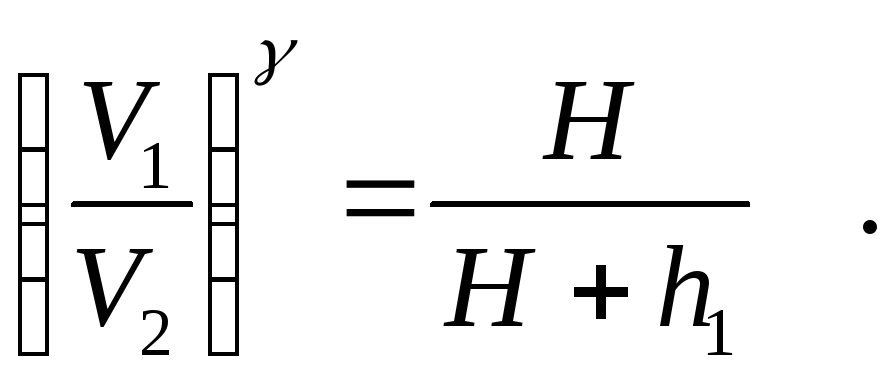(1)

Переход от конечного состояния С к начальному состоянию А можно было бы произвести изотермически, так как температура в обоих состояниях одинаковая – t_k..

Применим к этому переходу закон Бойля-Мариотта

(2)

Возводя левую и правую части уравнения (2) в степень γ, получим

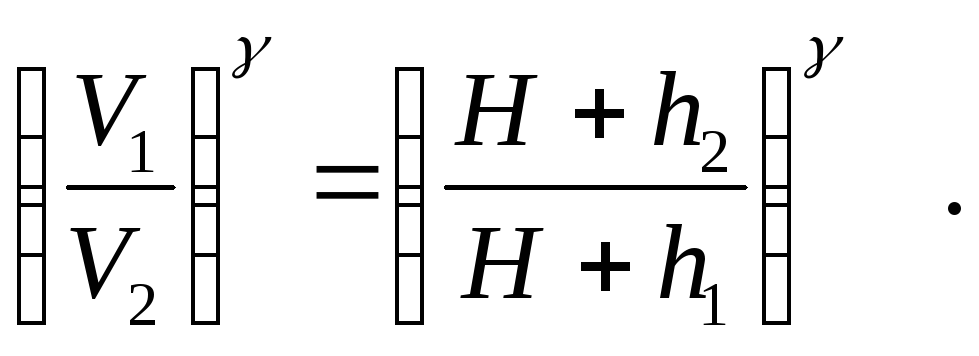(3)

Левые части равенств (1) и (3) равны, следовательно, равны и правые

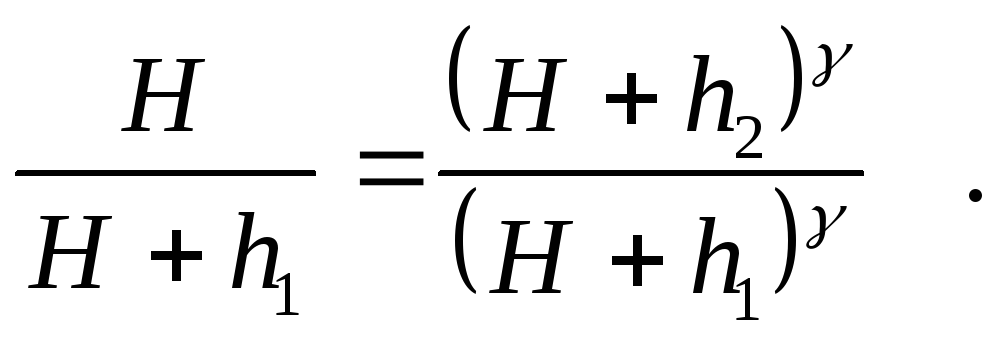(4)

Логарифмируя (4), получим

откуда

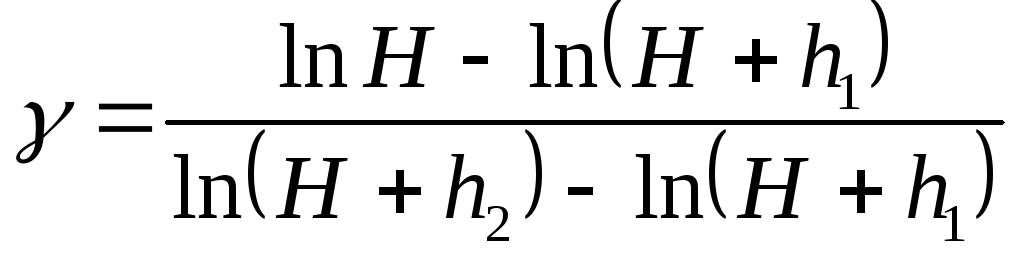
или

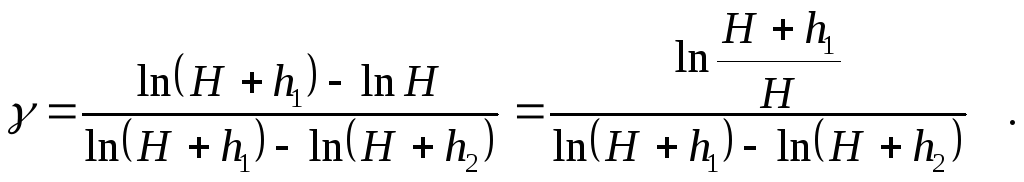
Вычитая и прибавляя в знаменателе последнего выражения ln H, получим

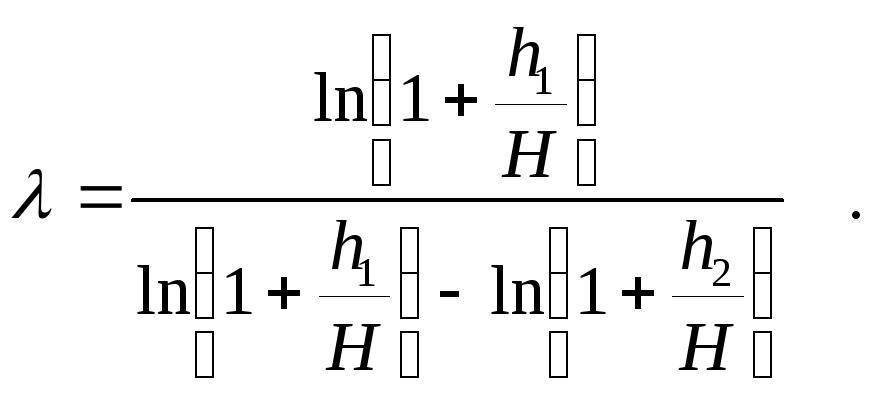
Из теории рядов известно, что выражение может быть представлено в виде

Если Х мало, то ln

В нашем случае

– достаточно малы и

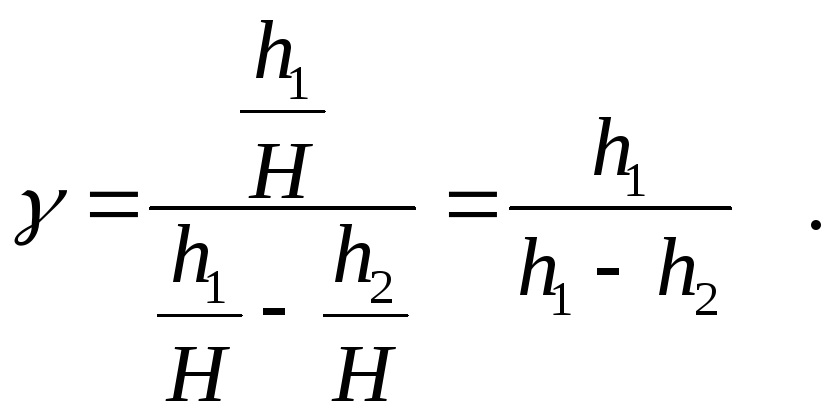
Формула (5) позволяет определить величину по двум показаниям манометраh₁ и h₂ .Опыт следует провести не менее пяти раз при различных показаниях для случаев расширения и сжатия воздуха в баллоне. Результаты измерений h₁ и h₂ занести в таблицу 3. Для каждой пары h₁ и h₂ по формуле (5) вычислить γ, полученные значения занести в таблицу. Вычислить приближенное значение γ, абсолютную и относительную погрешности. Окончательный результат записать в виде

Таблица 3

Результаты измерений и вычислений

	№ п/п	h1	h2
Сжатие	1 2 3 4 5
Расширение	1 2 3 4 5

Приближенное значение γ_пр

Абсолютная погрешность ∆γ

Контрольные вопросы

1. Что называется удельной и молярной теплоемкостями? Соотношение между ними. Единицы измерения.

2. Что такое С_v и что такое С_р ? Почему С_р > С_v ?

3. Какой процесс называется адиабатическим? Как практически можно осуществить адиабатический процесс?

4. Пользуясь первым началом термодинамики и уравнением Менделеева-Клапейрона, обосновать закон Пуассона для адиабатического процесса.

5. В системе координат P и V представьте адиабату и сопоставьте с изотермой. Почему адиабата идет более круто, чем изотерма?

6. Выведите расчетную формулу Клемана и Дезорма. Какие изопроцессы имели место в данной работе?

7. Проанализировать таблицы 1 и 2 для расширения и сжатия и выяснить физический смысл процессов.