2.4. Примеры решения задач

Задача № 1. Коаксиальный кабель имеет размеры d= 4 мм, D=12 мм. Заполняющей средой является диэлектрик с параметрами  = 2,4 и =1. Найти амплитуду напряжения в бегущей волне, если известно, что амплитуда тока составляет 0,4 А.

Решение: По формуле (2.1) находим

. Тогда .

Задача № 2

Коаксиальный кабель имеет политэтиленовую изоляцию ( = 2,25) и следующие размеры в поперечном сечении: D =3 мм, d =0,9 мм. Найти погонное затухание Т-волны в данном кабеле при частоте сигнала f = 750 МГц, считая, что =5,710⁷ См/м.

Решение: Погонное затухание а коаксиальном фидере определяется

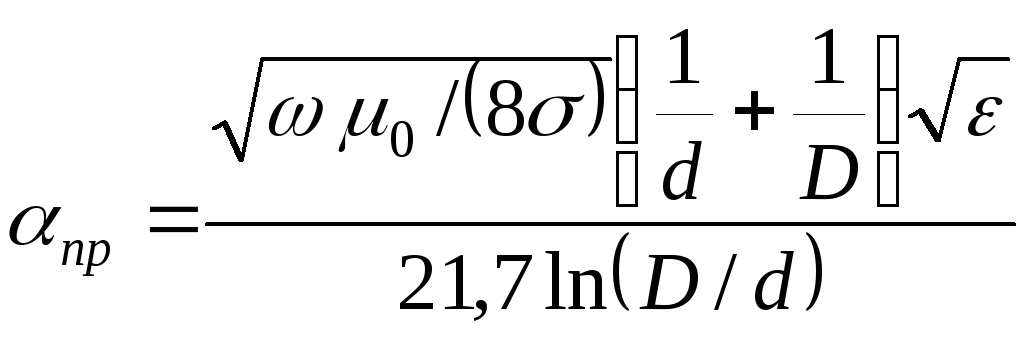(2.41)

Здесь значение параметра Ом. Тогда в соответствии с формулой (2.41)

дБ/м.

Задача № 3

Найти отношение между внешним и внутренним диаметрами коаксиальной линии передачи с волной типа Т, при котором будет ми­нимальное затухание. Считать, что потери в диэлектрике малы. Внутренний и внешний цилиндры выполнены из одного материала.

Решение.

Так как по условию задачи потери в диэлектрике малы, можем положить что  _д=0, тогда  = _м. Коэф­фициент ослабления _м в коаксиальной линии передачи определяем согласно формуле

м^-1 (2.42)

Поскольку R_s1=R_s2=R_s, из этой формулы находим

П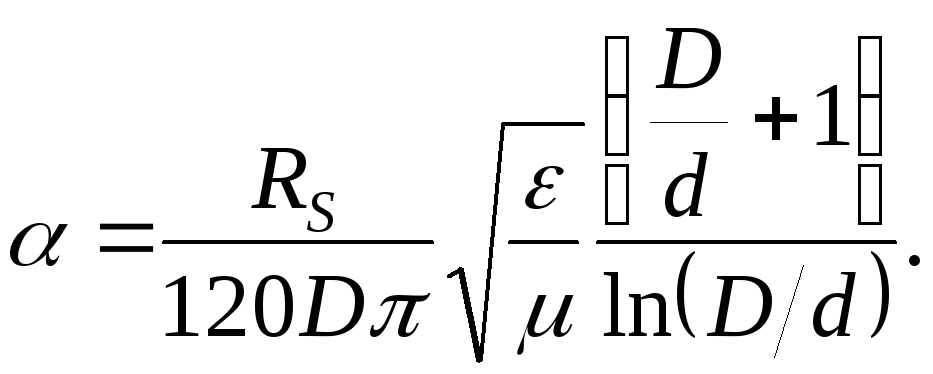реобразуем последнее выражение так, чтобы в него входило в яв­ном виде отношениеD/d:

(2.43)

Обозначив

запишем (2.44)

Для нахождения экстремума следует решить уравнение.

или

Полученное уравнение является трансцендентным.

Из графических построений (рис.2.5) имеем корень х = 3,6, откуда D/d == 3,6. Таким образом, минимальное затухание волны типа Т в коаксиальной линии передачи получается при отношении D/d = 3,6.

Задача № 4

Центрирование внутреннего цилиндра воздушного коаксиаль­ного волновода осуществляют c помощью диэлектрических шайб рис.(2.6). Рассчитать диаметр D внешнего цилиндра и глубину выточек h в нем, исходя из условия отсутствия отражений. Волновое сопротивле­ние линии Z_В=70 Ом, диаметр внутреннего цилиндра линии d = 4,5 мм, диаметр отверстия в шайбе d_ш=3,0 мм, относительная ди­электрическая проницаемость материала шайбы =2,3. Потерями в линии пренебречь.

Решение. Воздушную коаксиальную линию передачи c шайба­ми можно рассматривать как каскадное cоединение отрезков регуляр­ных линий. Поскольку в плоскости стыка шайбы и воздушной линии напряжение U является непрерывной функцией координаты z, мощность может быть целиком передана из од­ной линии в другую без отражения, если Z_В1= Z_В2 , где Z_В2- волновое сопротивление той части, где распо­ложена шайба.

Согласно выражению

(2.45)

запишем

откуда D = 14,45 мм. Далее находим

Приравнивая и , получаем уравнение

или

корень которого h = 1,58 мм.

Полученное решение является приближенным, поскольку не учиты­ваются локальные возмущения поля из-за скачков диаметров провод­ников.

Задача № 5.

Рассчитать волновое сопротивление, погонные емкость и ин­дуктивность, а также предельную передаваемую мощность в несимметричной полосковой линии передачи с воздушным заполнением. Па­раметры линии: ширина проводника b = 5 мм, расстояние между про­водником и заземленной пластиной d = 1 мм, толщина проводника t = 0,025 мм, предельно допустимое значение напря­женности электрического поля в воздухе.

Решение. Так как в нашем случае b/d > 2, то волновое сопротивление несимметричной полосковой линии передачи будет определяется выражением (2.22).

Полосковая линия передачи заполнена воздухом, для которого =1, =1. Тогда

Волновое сопротивление можно определить и по более упрощенной формуле, так как в рассматриваемом случае t/d = 0,025 << 1, а именно

Погрешность при этом не превышает 2,5%. Погонную емкость на­ходим по формуле:

а погонную индуктивность — из формулы .

После численных подстановок

Предельная передаваемая мощность в несимметричной полосковой линии передачи вычисляется по формуле (2.27).

При отношениях b/d=5 и t/d = 0,025 по табл.2.2 находим, что r_B=14,56.

Тогда

Полученное значение определяет предельную импульсную мощность. Конечно, средняя предельная мощность будет много меньше.

Задача № 6

Рассчитать коэффициент ослабления в симметричной полосковой линии передачи с твердым диэлектриком. Параметры линии: ши­рина проводникаb = 1,2 мм, расстояние между проводником и зазем­ленной пластиной d = 1 мм, толщина t = 0,05 мм. Проводники выполнены из меди. Параметры диэлектрика:

Рабочая частота 610⁹ Гц. .

Решение. Общие потери определяются суммой потерь в металле и диэлектрике  = _м +  _д . Коэффициент ослабления волны  _д за счет потерь в диэлектрике определя­ется формулой (2.32).

Так как

то

Коэффициент ослабления _м, обусловленный потерями в проводящих пластинах определяется по формуле (2.31) и равен 0,0979 м^-1.

Суммарный коэффициент ослабления:

Задача № 7

Определить затухание в однопроводном медном фидере, покрытом слоем полиэтилена ( = 2,3) толщиной ^/ = 5 мм, при диаметре провода 2r = 4 мм и длине волны  =40 см, если длина фидера l = 1 км.

Решение. Из графика рис.2.3 находим отношение r/r₀ =210^-2 , откуда предельный радиус

Волновое сопротивление фидера - табл.2.4

По формуле (2.33) определяем длину волны, распространяющейся вдоль фидера

По формулам (2.34) и табл.2.4 рассчитываем коэффициент затухания фидера

Ответ: l = 1,2210^-2 10³ дБ = 12,2 дБ.