111

4) 1-е плечо коаксиального симметричного 120⁰ тройника нагружено на сопротивление с коэффициентом отражения Г = 1/2. Определить [S] полученного четырехполюсника, ксв и тепловые потери в четырехполюснике при согласованной нагрузке в плече 3.

Ответ: ксв =1,333

5) Рассчитать размеры волноводно-щелевого моста на частоту 6 ГГц, записать его матрицу рассеяния. Определить комплексные амплитуды выходных сигналов, если на не развязанные входы моста подаются сигналы с амплитудами . Рассчитать матрицу рассеяния моста и выходные сигналы, при тех же входных, если частота увеличится на 20%

5. Характеристики и параметры антенн

5.1. Основные расчетные соотношения

Передающая антенна

Комплексная характеристика направленности передающей антенны по электрическому полю в дальней зоне, т.е. на расстоянии

, (5.1)

где a и b – максимальные размеры передающей и приемной антенн,

- длина волны,

в сферической системе координат описывается выражением

, (5.2)

в котором , , – соответственно амплитудная, поляризационная и фазовая диаграммы антенны.

Нормированные амплитудные ДН по напряженности поля и по мощности определяются соотношениями

, (5.3)

, (5.4)

где – значение амплитуды электрического поля в максимуме ДН. Часто нормированные ДН выражают в логарифмическом масштабе (в децибелах):

. (5.5)

Пространственное изображение нормированных амплитудных ДН имеет вид замкнутых поверхностей. По одной из координат обычно довольствуются сечениями ДН в двух главных плоскостях. Например, если рассматривают ДН как функцию от , то - в плоскостях  = 0 и  = /2. Сечение ДН главной плоскостью, содержащей электрический вектор, называют ДН в плоскости Е, а сечение главной плоскостью, содержащей магнитный вектор, - ДН в плоскости Н. Плоские сечения нормированных амплитудных ДН изображают как в полярных, так и в прямоугольных координатах, причем первый способ используют преимущественно для построения ДН слабонаправленных антенн, а второй – остронаправленных.

Из графического построения нормированных ДН определяют ширину главного лепестка (луча) на уровне 0,5 по мощности (0,707 по полю или –3 дБ в логарифмическом масштабе) 2_0,5 , положения нулей, а также уровень боковых лепестков и их направления, гдеq – номер бокового лепестка.

Поляризация передающей антенны определяется поляризацией ее поля излучения по электрическому вектору. Наиболее общим случаем поляризации является эллиптическая поляризация, которая полностью описывается следующими параметрами поляризационного эллипса:

• углом_э наклона большой оси эллипса к орту 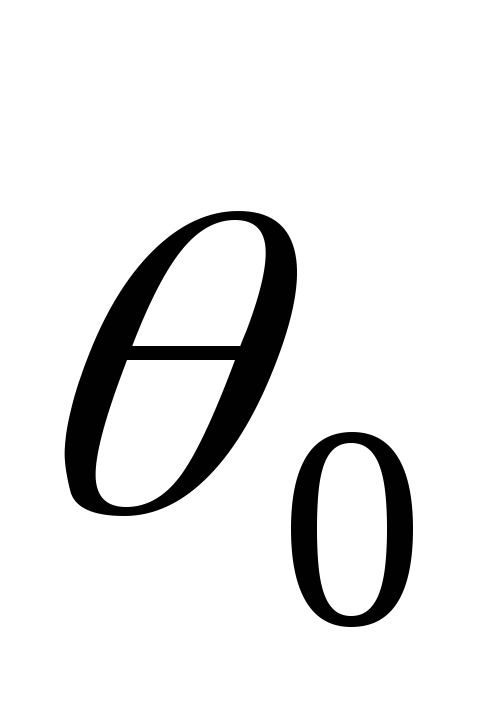сферической системы координат(0  _э   / 2);

• коэффициентом эллиптичности поляризации

, (5.6)

где b и a – малая и большая полуоси эллипса (0  K_Э  1);

• знаком поляризации , который указывает на направление вращения электрического вектора в плоскости эллипса:– для правой поляризации и– для левой.

При эллипс вырождается в прямую линию, и поле имеет линейную поляризацию; приэллипс становится окружностью и поле имеет круговую поляризацию.

Параметры поляризационного эллипса при известных компонентах излучаемого поля определяются по формулам

; (5.7)

, (5.8)

где- отношение амплитуд ортогональных компонент,

–разность фаз комплексных амплитуд этих компонент.

Обратные зависимости имеют вид

; (5.9)

. (5.10)

Зависимость коэффициента эллиптичности от угловых координат точки наблюдения называют поляризационной диаграммой антенны.

Знание амплитудной и поляризационной диаграмм передающей антенны позволяет определить ее КНД. Для антенны линейной поляризации КНД по отношению к изотропному излучателю в направлении максимума ДН определяется выражением

. (5.11)

Для антенны эллиптической поляризации при совпадении максимумов парциальных ДН выражение для КНД имеет более сложный вид

, (5.12)

где

- парциальный КНД для компоненты поля ,

- парциальный КНД для компоненты поля .

Здесь и- нормированные амплитудные ДН взаимно ортогональных компонент.

На практике применяют приближенную оценку КНД по формуле

, (5.13)

где и- ширина ДН антенны на уровне 0,5 по мощности в главных плоскостях в радианах.