Решение

• Для скачка волнового сопротивления нормированная матрица рассеяния имеет вид:

(4.27)

Для отрезка линии передачи нормированная и ненормированная матрицы совпадают, поскольку волновые сопротивления в обоих плечах одинаковы.

, (4.27)

где k - постоянная распространения в линии передачи.

• Используем связь между матрицами рассеяния и передачи (4.4) и (4.5)

Определим элементы матрицы передачи для скачка сопротивлений

Таким образом, для скачка волновых сопротивлений получим

(4.29)

Аналогично определиться матрица передачи для отрезка линии

(4.30)

• Перемножим матрицы передачи по правилам умножения матриц (строка на столбец). Например,

В итоге для объединенной матрицы передачи получим

(4.31)

• Перейдем по формуле (4.5) к объединенной матрице рассеяния

.

Вычислим определитель матрицы []

.

Таким образом, получим

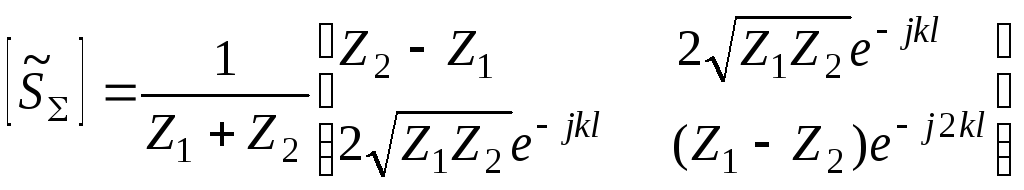(4.32)

• Проанализируем полученную формулу

 Матрица является симметричной, что является следствием взаимности устройства.

 Матрица является унитарной, что является следствием недиссипативности устройства. Действительно, чтобы матрица была унитарной необходимо выполнение условий (4.23):

1) сумма квадратов модулей элементов каждого столбца равна единице,

2) сумма произведений элементов одного столбца на комплексно сопряженные элементы другого столбца равна нулю.

Проверим эти условия. При этом необходимо помнить, что волновые сопротивления линий – чисто вещественные числа и что модуль от экспоненты с мнимым показателем всегда равен единице (при любом вещественном)

Аналогично и для второго столбца.

Проверку второго условия – выполнить самостоятельно.

• Конечно, матрицу [S] данного устройства можно было получить сразу из матрицы [S] скачка сопротивлений (4.27),учитывая, что добавление отрезка линии эквивалентно переносу плоскостей отсчета (см. раздел 3.4 курса лекций).

• Получим ненормированную матицу устройства, используя формулы (4.6)

В результате ненормированная матрица [S] будет

(4.33)

Матрица стала несимметричной и неунитарной, что и следовало ожидать по теории.

4.2.2. Шестиполюсники

Задача №4

Определить матрицу рассеяния коаксиального (или полоскового) тройника с волновыми сопротивлениями плечZ₁ и Z₂, как показано на рис.4.5. Длины линий передач в плечах тройника будем считать равными нулю.

Рис.4.5

Решение.

• Задачу можно решать как для ненормированной, так и для нормированной матриц. В обоих случаях следует вначале определить коэффициенты на главной диагонали матрицы, т.е. S₁₁, S₂₂, S₃₃,поскольку это наиболее просто и остальные коэффициенты выражаются через них.

• Начнем с S₁₁. Согласно определению (4.3)

Это означает, что S₁₁является коэффициентом отражения со стороны плеча 1 при условии, что плечи 2 и 3 нагружены на активные сопротивления равные волновым сопротивлениям линий передач в плечах 2 и 3.(рис.4.6)

Рис.4.6

Поскольку плечо 1 нагружено на параллельное соединение сопротивлений Z₂, то коэффициент отражения со стороны плеча 1 согласно (4.10) будет

. (4.34)

• Определим S₂₂ и S₃₃. Из-за симметрии плеч 2 и 3, эти коэффициенты равны. Определим их так же, как и S₁₁. Нагрузкой для плеча 2 является параллельное соединение сопротивлений Z₁ и Z₂.

Таким образом, коэффициент отражения со стороны плеча 2 будет

(4.35)

Коэффициенты S₁₁,S₂₂иS₃₃не изменяются при нормировке матриц. Остальные коэффициенты определяются для нормированных и ненормированных матриц различными способами.