Решение.

• Вспомним определение коэффициентов матрицы рассеяния. Согласно (4.3),

S₁₁ – коэффициент отражения от четырехполюсника со стороны плеча 1 при согласованном плече 2.

S₂₁ – коэффициент передачи по напряжению при том же условии.

• Ч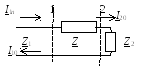то означает “согласованное плечо 2”? Это означает, что плечо 2 нагружено на активное сопротивление, равное волновому сопротивлению линии передачи в плече 2. (рис.4.2).

Рис.4.2

Коэффициент отражения (по напряжению) в любой линии передачи определяется по формуле (4.10)

В данной схеме роль Z_H играет Z +Z₂ , а роль Z_В – Z₁. Таким образом,

(4.17)

Для определения коэффициента передачи из плеча 1 в плечо 2 (S₂₁) учтем, что токи слева и справа от сопротивленияZравны (I₁=I₂). Кроме того, ток на входе 1 складывается из тока падающей и отраженной волн, а на входе 2 – является током только отраженной волны.

Токи и напряжения в падающей и отраженной волнах в 1 плече связаны через Z₁ , а в плече 2 – через Z₂

. (4.18)

Подставим (4.18) в равенство токов ()

.

Поделим это уравнение на U_1П

(4.19)

Подставим выражение для S₁₁

(4.20)

• Выражения для S₂₂ и S₁₂ получим заменой “1” на “2” в формулах (4.17) и (4.20). В результате, матрица рассеяния будет иметь вид

(4.21)

Видно, что матрица несимметричная (S₁₂S₂₁).Должна ли она быть унитарной? Очевидно, нет, т.к. сопротивление Z может быть диссипативным и, кроме того, матрица S – ненормированная. Поскольку S₁₁S₂₂ ,то несимметричным является и сам четырехполюсник, т.е. его свойства со стороны плеч 1 и 2 различны. Убедитесь самостоятельно, что при чисто реактивном сопротивлении Z=jX модули коэффициентов S₁₁ и S₂₂ равны, а фазы имеют противоположные знаки.

• Перейдем к нормированной матрице по формуле (4.6)

.

Очевидно, что нормировка не изменяет диагональные элементы матрицы, для которых , т.е. коэффициенты S₁₁ и S₂₂

Определим

;

.

Таким образом,

. (4.22)

Видно, что матрица стала симметричной относительно главной диагонали. Это и следовало ожидать, так как устройство – взаимное. Можно убедиться, что если Z – чисто реактивное, то выполняются и условия унитарности, т.е.

(4.23)

• Если волновые сопротивления линий одинаковы , то матрицы нормированная и ненормированная совпадают

, (4.24)

где - сопротивлениеZ, нормированное к волновому сопротивлению Z_В. При этом четырехполюсник, конечно, становится симметричным (S₁₁=S₂₂ )

• Отметим, что формулу для матрицы рассеяния при разных волновых сопротивлениях линий можно также получить через матрицы передачи последовательного сопротивления в однородной линии и скачка волновых сопротивлений. Однако в данном случае выбранный способ является более коротким.

Задача №2

О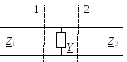пределить матрицу рассеяния проводимостиY, параллельно включенной в разрыв двух линий передач с волновыми сопротивлениями Z_B1 и Z_B2. Будем для краткости обозначать волновые сопротивления линий просто Z₁ и Z₂.

Рис.4.3

Решение.

• Порядок решения этой задачи аналогичен предыдущей. Сначала определяется S₁₁, однако в формуле (4.10) для коэффициента отражения Г лучше перейти от сопротивлений к обратным величинам- проводимостям

(4.25)

• При определении S₂₁ следует использовать равенство не токов, а напряжений по обеим сторонам проводимости. Это приводит к соотношению

.

Опуская промежуточные выкладки и выражения для нормированной матрицы (приведено в лекции) и ненормированной, ограничимся случаем одинаковых волновых сопротивления, когда нормированная и ненормированная матрицы совпадают.

(4.26)

Последнюю формулу рекомендуется получить самостоятельно.

Задача №3

Определить матрицу рассеяния каскадного соединения двух четырехполюсников: скачка волнового сопротивления (1) и отрезка линии передачи длиной(2).

Рис.4.4

Матрицы рассеяния обоих элементов будем считать известными.