86

11. Реактивное сопротивление индуктивного стержня, установленного в волноводе сечением аb = 5,82.5 см, на расстоянии от узкой стенки волновода,X_L= 1725 Ом. Частота генератора f=4000 МГц. Определить диаметр стержня.

Ответ: 2r = 4 мм.

4. Матричный анализ свч-устройств

4.1. Основные расчетные соотношения

Матрица рассеяния связывает напряжения падающих и отраженных волн на входах (плечах) многополюсника

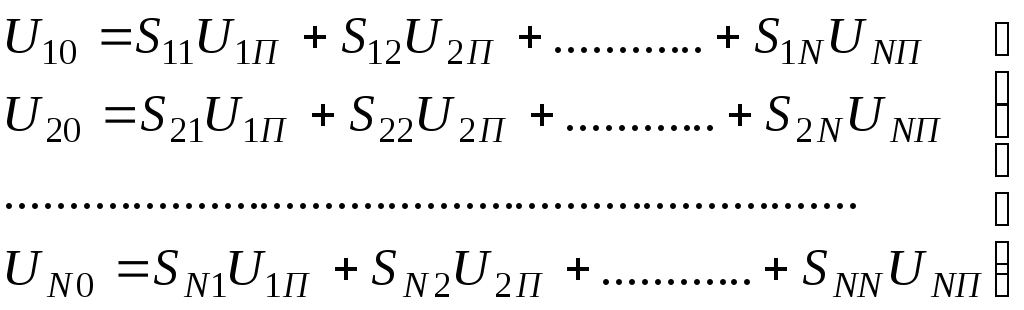, (4.1)

где U_k0, U_kП  напряжения отраженных и падающих волн в плече “k” многополюсника, S_i,k  коэффициенты матрицы рассеяния.

Только для четырехполюсника может быть составлена матрица передачи, которая связывает напряжения падающих и отраженных волн на его входах

(4.2)

Коэффициенты матрицы рассеяния имеют вполне определенный физический смысл, как коэффициент отражения от данного плеча и волновой коэффициент передачи по напряжению между двумя плечами при согласованных остальных плечах.

(4.3)

Между матрицами рассеяния и передачи четырехполюсника существует связь, определяемая соотношениями:

(4.4)

(4.5)

При различных волновых сопротивлениях плеч многополюсника во многих случаях следует перейти к нормированным матрицам с коэффициентами

, , (4.6)

Нормированные матрицы рассеяния обладают двумя важными свойствами:

Свойство 1. Взаимному многополюснику соответствует симметричная нормированная матрица рассеяния .

Свойство 2. Недиссипативному многополюснику соответствует унитарная нормированная матрица рассеяния . Унитарной матрицей называется такая матрица, для которой произведение транспонированной матрицы на комплексно-сопряженную матрицу равно единичной матрице

(4.7).

Соотноешния (4.4) и (4.5) сохраняются для нормированных матриц.

Матрица рассеяния взаимного, реактивного (недиссипативного) четырехполюсника характеризуется тремя вещественными параметрами

. (4.8)

Выбором положения входов (плоскостей отсчета) их число может быть уменьшено до одного.

Коэффициент отражения от четырехполюсника, нагруженного на сопротивление Z_Н, определяется соотношением

, (4.9)

где коэффициент отражения от нагрузки равен

(4.10)

Матрицы рассеяния согласованных со стороны Е и Н плеч волноводных тройников имеют вид

, (4.11)

Для несогласованного коаксиального или полоскового тройника с одинаковыми волновыми сопротивлениями плеч матрица рассеяния представляется в виде

(4.12)

Матрицы рассеяния синфазно-противофазного и квадратурного мостов могут быть представлены в виде

(4.13)

Длина щели волноводно-щелевого моста определяется из выражения для разности фаз волн Н₁₀ и Н₂₀ в плечах моста

, (4.14)

при которой разность фаз равна 90⁰.

Условия согласования квадратного и кольцевого мостов имеют вид

, (4.15)

где Z₁ и Z₂ – волновые сопротивления плеч мостов, Z –волновое сопротивление подводящих линий.

Направленный ответвитель на связанных линиях будет согласован при выполнении условия

, (4.16)

где - волновые сопротивления области связи для четного и нечетного типов волн.

Для закрепления материала этой темы и приобретения навыков решения задач рассмотрим несколько примеров. Рекомендуется все задачи разбирать «с карандашом в руках», повторяя все выкладки самостоятельно. На рисунках пунктиром обозначены входы (плоскости отсчета) многополюсников. Необходимо помнить, что отрезки линий передач на СВЧ являются самостоятельными четырехполюсниками. Знаком отмечены отдельные этапы решения задач.

4.2. Примеры решения типовых задач

4.2.1. Четырехполюсники

Задача №1

Определить матрицу рассеяния сопротивления Z последовательно включенного в разрыв двух линий передач с волновыми сопротивлениями Z_B1 и Z_B2. Будем для краткости обозначать волновые сопротивления линий просто Z₁ и Z₂.

Рис.4.1

Длину подводящих линий будем считать раной нулю.