3.6.3. Коэффициент отражения от нагруженного

четырехполюсника

Определим коэффициент отражения от четырехполюсника с известной матрицей рассеяния, нагруженного на сопротивление Z_H.

Рис. 3.5

Для упрощения будем считать волновые сопротивления линии передач на входах четырехполюсника одинаковыми. В этом случае нормированная и ненормированная матрицы совпадают. Определим коэффициент отражения от входа 1 ( Г ) с учетом сопротивления нагрузки Z_H. Запишем соотношения между [ U_П ] и [ U₀ ] для четырехполюсника.

,

. (3.44)

Соотношения между U_2П и U₂₀ определяются коэффициентом отражения от нагрузки Г_Н.

. (3.45)

Здесь учтено, что отраженная волна для четырехполюсника является падающей для нагрузки и наоборот. Совместное решение (3.44) и (3.45) дает значение коэффициента отражения на входе 1 при наличии нагрузки в плече 2.

. (3.46)

Соотношение (3.46) используется при экспериментальном определении матрицы [S] четырехполюсника. Чтобы определить четыре элемента матрицы (S₁₁ ,S₁₂ ,S₂₁,S₂₂) достаточно измерить четыре значения коэффициента отражения Г при разных значениях Г_Н, соответствующих разным нагрузкам Z_H. В качестве нагрузок с известными значениями Z_Н можно использовать короткозамкнутые отрезки разной длины.

Полученная система из четырех нелинейных уравнений может быть решена численно или графически (метод Дешана [4]).

Согласующие устройства в виде шлейфов и четвертьволновых трансформаторов могут рассматриваться как согласующие реактивные, взаимные четырехполюсники, включенные по схеме рис. 3.5. Соотношение (3.46) позволяет объяснить их работу с физической точки зрения. Действительно, выбирая матрицу [ S ] вида ( 3.43 ), т.е. предполагая согласующий четырехполюсник взаимным, реактивным и симметричным ( S₁₁ = S₂₂ ), получим

,

.

Подставим эти значения в (3.46) и, полагая Г = 0, приходим к соотношению

Таким образом, согласующее устройство должно создавать отраженную волну (будучи нагруженным на согласованную нагрузку) с такой же амплитудой, как и в отраженной волне от нагрузки

и фазой противоположного знака

₁₁ = -_Н.

Другими словами, волны отраженные от нагрузки и от согласующего устройства должны взаимно компенсироваться. По этому принципу работают большинство реактивных согласующих устройств.

3.7. Шестиполюсники свч

3.7.1. Общие теоремы

Шестиполюсником называется устройство, содержащее 3 входа (6 полюсов). Типичными примерами шестиполюсников являются, так называемые, тройники волноводные, коаксиальные и полосковые, которые будут рассмотрены ниже. Вначале докажем теорему, общую для шестиполюсников любых конструкций.

Теорема: Взаимный реактивный шестиполюсник не может быть согласован по всем входам с помощью реактивных согласующих устройств.

Доказательство: Предположим обратное, т.е. что с помощью включения реактивных согласующих устройств удалось добиться полного согласования по всем входам, что соответствует условию

.

Рис.3.6

Запишем матрицу , с учётом взаимности шестиполюсника

(3.47)

Поскольку шестиполюсник – недиссипативный (реактивный), то условие унитарности дает

; ;.

Очевидно, что какие-то два коэффициента из трех (S₁₂, S₁₃, S₂₃) должны быть равны 0. Пусть это будут S₁₂ и S_13, но тогда не выполняется ещё одно условие унитарности

.

Таким образом, матрица вида (3.47) не может быть одновременно симметричной и унитарной, что и доказывает теорему.

У этой теоремы есть два важных для практики следствия.

Следствие 1: Согласование двух плеч во взаимном реактивном шестиполюснике превращает его во взаимный реактивный четырёхполюсник, т. к. передача энергии в несогласованное плечо отсутствует.

Доказательство: Пусть в матрице (3.47)

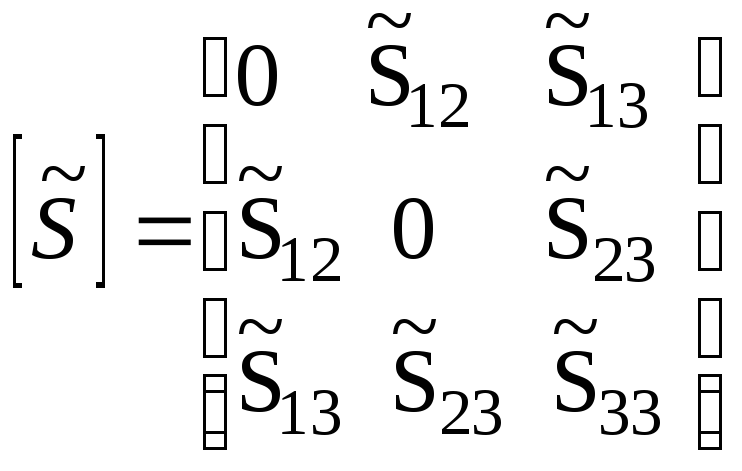
Условие унитарности матрицы приводит к уравнениям

Из первых трёх уравнений следует и. Тогда из последнего уравнения следует. Таким образом, матриц рассеяния принимает вид

Поскольку , то из полученной матрицы следует, что если подавать энергию в первое плечо, то она полностью передаётся во второе () и не поступает в третье (). То же со стороны второго плеча. Если же подать энергию в третье плечо, то она полностью отразится (). Таким образом, если теорема утверждает, что согласование взаимного реактивного шестиполюсника по всем входам невозможно, то следствие 1 -что согласование двухвходов хотя и возможно, но лишено смысла, т.к. несогласованный вход оказывается фактически отключенным от шестиполюсника.

Следствие 2: Согласованный по всем входам невзаимный реактивный шестиполюсник является идеальным циркулятором.

Доказательство. Если в условии теоремы отказаться от условия взаимности многополюсника, то он может быть согласован по всем входам. Запишем для этого случая матрицу рассеяния, учитывая, что

Условие унитарности матрицы приводит к уравнениям

; ;.

Пусть , тогда. Далее следует, чтоии далее. Таким образом, получаем

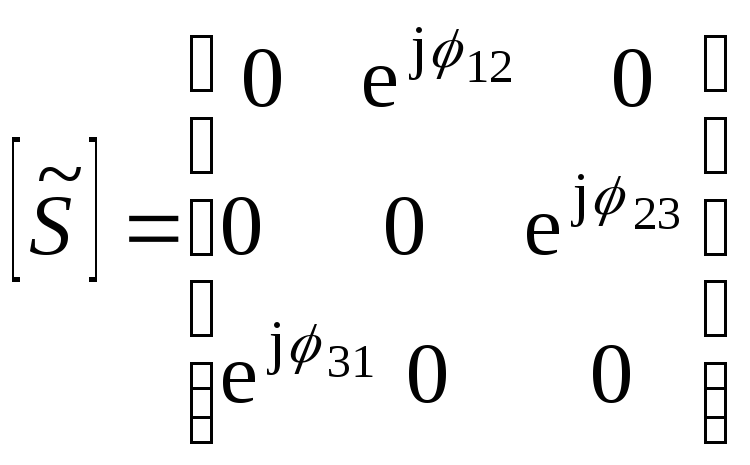(3.48)

Фазовые коэффициенты характеризуют сдвиг по фазе при прохождении волны внутри тройника. Чтобы проследить направления передачи энергии в таком устройстве, подадим её сначала в первое плечо, а остальные нагрузим согласованными нагрузками. Передача энергии будут определяться первым столбцом матрицы (3.48) . Посколькуи, то энергия будет полностью поступать в плечо 3. Аналогичные рассуждения, а именно коэффициенты третьего столбца, показывают, что из третьего плеча энергия будет полностью поступать во второе, а из второго – в первое. Устройства с такими направлениями распространения энергии называются идеальными циркуляторами. Для своей работы они требуют наличия внутри их невзаимного элемента, например, намагниченного феррита. Примерами таких циркуляторов могут служить волноводныеY – циркуляторы, которые применяются для развязки генераторов и усилителей от нагрузки, в антенных коммутаторах и т.п.