3.6. Двух и четырехполюсники свч

3.6.1. Двухполюсники свч

Двухполюсники, т.е. устройства, имеющие один вход, являются оконечными нагрузками линий передач. Для описания их свойств достаточно одного параметра – сопротивления нагрузки Z_Н и связанного с ним комплексного коэффициента отражения Г, который играет роль матрицы рассеяния двухполюсника. Связанные с этим вопросы согласования с использованием диаграммы Вольперта были рассмотрены выше в главе 2 данного курса. В диапазоне СВЧ двухполюсниками являются различные нагрузки линий передач: согласованные нагрузки коаксиальные и волноводные, короткозамыкатели, детекторные секции и т.п. Передающие антенны для линий передачи являются нагрузками и, таким образом, также двухполюсниками. Описание волноводных, коаксиальных и полосковых короткозамыкателей и согласованных нагрузок можно найти в [2,4,5,6]

3.6.2. Элементарные четырехполюсники свч

К четерехполюсникам СВЧ относятся многочисленные устройства:

• переходы с одной линии передачи на другую: волноводно – коаксиальные, волноводно – полосковые и т.п.;

• переходы между линиями одного типа, но разных размеров, так называемые, скачки волновых сопротивлений;

• фильтры;

• фазовращатели, аттенюаторы, вентили;

• согласующие устройства, рассмотренные в главе 2;

• резонаторы, включенные на проход.

Усилители также являются четырехполюсниками, но активными. Здесь мы ограничимся лишь пассивными устройствами. Описание конструкций конкретных типов четырехполюсников можно найти в [2,3,4,5]. При анализе сложных устройств их обычно разделяют на простейшие элементы с известными матрицами или, по которым затем определяют общую (объединенную) матрицу рассеяния (метод декомпозиции, рассмотренный ниже, в разделе 3.9).

В зависимости от соотношения между коэффициентами ,могут быть различные типы четырехполюсников и их матриц рассеяния:

• если , то четырехполюсник - взаимный, а матрица- симметричная;

• если выполняются условия унитарности (3.33), то матрица – унитарная, а четырехполюсник - реактивный (без потерь);

• если ито четырехполюсник – симметричный;

• если ито четырехполюсник – антимметричный;

• если условия симметричности или антиметричности не выполняются, то четырехполюсник – несимметричный.

Приведём матрицы некоторых элементарных четырёхполюсников. Способ составления некоторых из них перенесен на практические занятия.

а) Отрезок линии передачи без потерь с вещественной постоянной распространения  и длиной-

(3.34)

Четырехполюсник – взаимный, реактивный, симметричный. Матрица – симметричная, унитарная.

б) Отрезок линии передачи с потерями с комплексной постоянной распространения и длиной-

(3.35)

Четырехполюсник – взаимный, диссипативный, симметричный. Матрица – симметричная, неунитарная.

в) Идеальный трансформатор с коэффициентом трансформации n, Z_В1 и Z_В2- волновые сопротивления входной и выходной линий передач

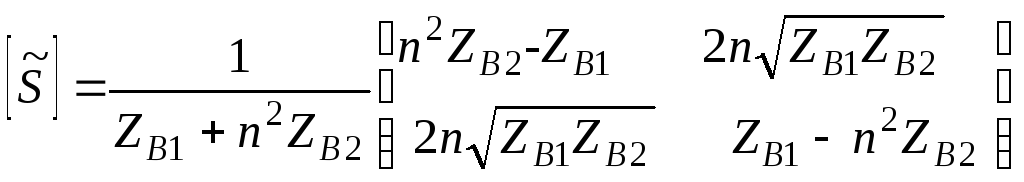
(3.36)

Четырехполюсник – взаимный, реактивный, антиметричный. Нормированная матрица – симметричная, унитарная.

Запишите ненормированную матрицу рассеяния и обьясните причину того, что она стала несимметричной и неунитарной.

г) Идеальный вентиль – устройство, которое пропускает энергию без поглощения в одном направлении и полностью поглощает в другом.

(3.37)

Четырехполюсник – невзаимный, диссипативный, несимметричный. Матрица – несимметричная, неунитарная.  - сдвиг фазы волны в прямом направлении.

д) Идеальный невзаимный фазовращатель – устройство, создающее сдвиг по фазе между входным и выходным напряжением, зависящий от направления распространения волны.

(3.38)

Четырехполюсник – невзаимный, реактивный, несимметричный. Матрица – несимметричная, унитарная.

е) Сопротивление Z= R+jX , последовательно включенное в линию с волновым сопротивлением Z_B. Длина подводящих отрезков линий считается равной 0.

, (3.39)

где - нормированное к волновому сопротивлению линии сопротивлениеZ.

Четырехполюсник – взаимный, диссипативный при R 0 и реактивный при R= 0, симметричный. Матрица – симметричная, неунитарная при R 0 и унитарная при R= 0.

ж) Проводимость Y=G+jB, включенная параллельно в линию с волновым сопротивлением Z_B. Длина подводящих отрезков линии считается равной 0.

, (3.40)

где - нормированная проводимость.

Четырехполюсник – взаимный, диссипативный при G 0 и реактивный при G= 0, симметричный. Матрица – симметричная, неунитарная при G 0 и унитарная при G= 0.

з) Скачок волнового сопротивления. Длины подводящих линий считаются равными 0.

(3.41)

Обратите внимание на то, что в данном случае записана нормированная матрица рассеяния. В большинстве предыдущих случаев это не имело значения, т.к. волновые сопротивления плеч были одинаковы.

Четырехполюсник – взаимный, реактивный, антиметричный. Матрица – симметричная, унитарная.

Проверьте самостоятельно унитарность матрицы формулы (3.41). Перейдите к ненормированной матрице и проверьте условие унитарности для нее. Объясните полученный результат.

и) Взаимный реактивный ( недиссипативный ) четырехполюсник, согласно условиям унитарности и симметричности матрицы (), имеет матрицу, содержащую всего три вещественных параметра. Она может быть представлена, например, в таком виде

, (3.42)

где -некоторый параметр, определяющий отношение коэффициентов отражения и передачи.

В зависимости от вида такого четырехполюсника возможны следующие варианты.

1.  = 90⁰, .

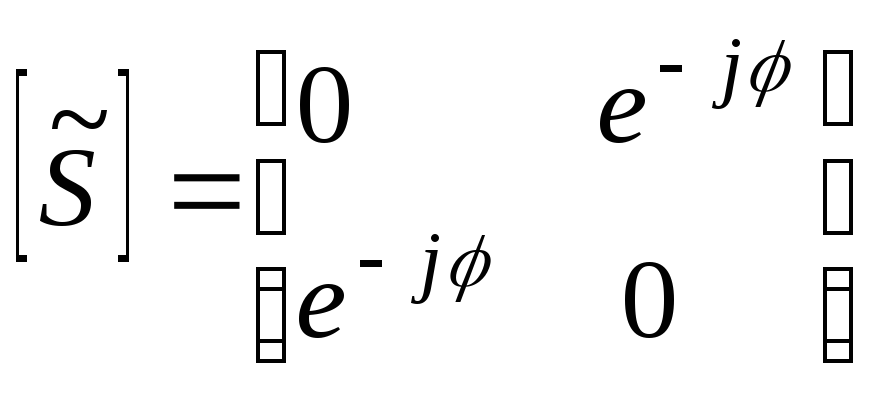Примером является отрезок линии передачи длиной .

2. ₁= ₂ =0,  соответствует скачку волновых сопротивлений.

3) Из (3.42) следует, что, поскольку. Отсюда следует, что.

Если учесть, что , то это приводит к матрице вида

. (3.43)

Знак плюс или минус перед иопределяется конкретным типом четырехполюсника. В частности, такую матрицуимеют последовательно включенныеZ и параллельно включенные Y , при их чисто реактивном характере. Убедитесь самостоятельно, что при Z=jX справедливы соотношения

,

при этом в формуле (3.43) следует брать знак плюс.