Таким образом,

(3.24)

Аналогичные соотношения получаются для и.

Таким образом, при отодвигании плоскостей отсчета от многополюсника меняются лишь фазы коэффициентов S_ik, уменьшаясь на величины ₁l₁ и ₂ l₂ согласно (3.24). Это свойство можно использовать для выбора положения плоскостей отсчета, чтобы изменять фазы коэффициентов S_ik.

3.5.Свойства многополюсников и их матриц [s]

Нормированные матрицы обладают двумя замечательными свойствами, связанными с физическими свойствами многополюсников.

Свойство 1. Взаимному многополюснику соответствует симметричная нормированная матрица рассеяния .

Из общей теории электрических цепей известно, что для взаимного многополюсника должно выполняться соотношение

Y_{k i} = Y_{i k}, (3.25)

т.е. матрица проводимости взаимного многополюсника симметрична относительно главной диагонали. Аналогичным свойством будет обладать согласно (3.22) и нормированная матрица . Из соотношений ( 3.23 ) междуиследует, что в этом случае

(3.26)

Т.е. нормированная матрица также симметрична относительно главной диагонали. Соотношение (3.26) означает, что внутри многополюсника передача энергии междуi- ым и k -ым входами не зависит от направления передачи энергии. Взаимность многополюсника определяется по отсутствию внутри его невзаимных элементов: диодов, транзисторов, намагниченных ферритов и плазмы и обычно легко определяется самим типом многополюсника.

Свойство 2. Недиссипативному многополюснику соответствует унитарная нормированная матрица рассеяния .

Недиссипативным (реактивным) многополюсником называется многополюсник, внутри которого отсутствуют потери энергии. Конечно, реально внутренние потери всегда присутствуют, но они могут быть пренебрежимо малы по сравнению с общей мощностью на входах многополюсника.

Очевидно, что для недиссипативного многополюсника закон сохранения энергии может быть записан так

, (3.27)

т.е. суммы мощностей всех падающих и отраженных волн должны быть равны. Обозначим

вектор-столбец нормированных напряжений падающих волн и - вектор- строка этих же напряжений (знак “Т” означает транспонирование матрицы). Тогда, согласно правилу перемножения матриц,

, (3.28)

где знак “*” означает комплексно – сопряженную матрицу. Аналогично для отраженных волн, сумма их мощностей во всех плечах может быть записана в виде

. (3.29)

Подставим в (3.27) соотношение и учтем, что при транспонировании произведения матриц меняется их порядок в произведении

. (3.30)

Приравнивая (3.28) и (3.30) приходим к соотношению

. (3.31)

Из него следует, что для недиссипативных (реактивных) многополюсников и их нормированных матриц рассеяния должно быть справедливо следующее утверждение:

Произведение транспонированной матрицы на комплексно-сопряженную матрицу должно давать единичную матрицу (матричную единицу), т.е.

, (3.32)

где [Е] – единичная матрица, у которой все элементы главной диагонали равны 1, остальные есть 0. Матрицы, удовлетворяющие условию (3.32), в математике называются унитарными.

Выясним, к чему приводит свойство унитарности матрицы на примере недиссипативного четырехполюсника. Запишем исходную, транспонированную и комплексно-сопряженную матрицы, а также условие унитарности (3.32)

,,

Раскрывая произведение матриц, получаем систему уравнений

(3.33)

Третье и четвертое уравнения в (3.33) тождественны, поэтому фактически имеем три независимых уравнения. Общее правило их составления можно сформулировать в виде:

1. Сумма квадратов модулей элементов каждого столбца унитарной матрицы равна 1.

2. Сумма произведений элементов одного столбца на комплексно-сопряженные элементы другого равна 0.

Нетрудно видеть, что первое правило отражает закон сохранения энергии для каждого входа многополюсника при условии согласования остальных плеч.

Действительно, представим, что на 1-ый вход 2N- полюсника падает мощность 1 Вт (рис.3.4), что соответствует . Остальные плечи нагружены на свои согласованные нагрузки. Тогда очевидно

т.е. сумма мощностей, уходящих от многополюсника волн, должна давать 1 Вт.

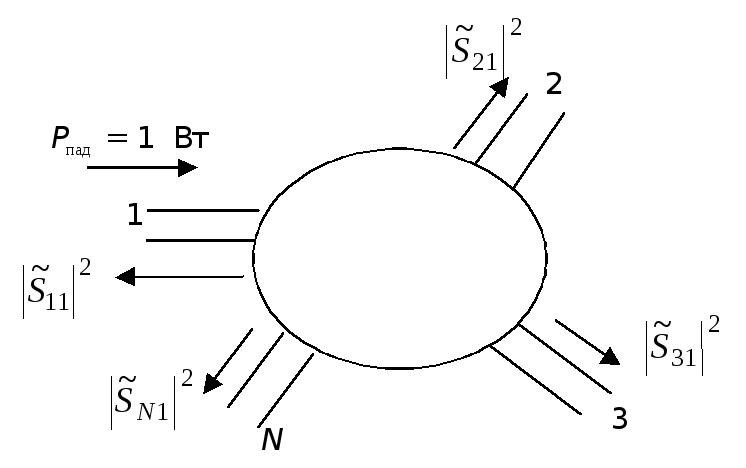
Рис.3.4

Свойство недиссипативности, так же как взаимности, в большинстве случаев является очевидным. Использование этих свойств в сочетании с использованием свойства симметрии многополюсника значительно облегчают задачу определения его матрицы . Далее мы рассмотрим применение этих общих положений теории многополюсников для анализа конкретных устройств СВЧ, разделяя их по числу полюсов (входов).