69

нет нераспространяющихся типов волн. Наконец, будет рассматриваться режим установившихся колебаний (стационарный процесс).

Перейдем к выводу основных параметров, характеризующих режим бегущей волны в линиях конечной длины при отсутствии потерь.

Коэффициент отражения. Пусть имеется некоторая линия передачи, характеризующаяся волновым сопротивлением и постоянной распространения, на одном конце которой в сечении а-а включен согласованный генератор, на другом некоторая нагрузка (см. рис 2.2). Генератор создает в линии бегущие в направлении оси l волны , и , .

U^пад или U⁺ - падающая волна напряжения; или - падающая волна тока. Нагрузка приводит к возникновению в линии бегущих в противоположном направлении оси l отраженной волны напряжения U^отр или U^ и отраженной волны тока или . (В волноводах с одним типом волн UE, IH).

В произвольном сечении линии l полное напряжение и полный ток равны:

(2.1)

(2.2)

Отношение напряжения отраженной волны к напряжению падающей в некотором сечении линии l называется коэффициентом отражения по напряжению

. (2.3)

Также определяется коэффициент отражения по току

, который равен ^*)

Запишем уравнения (2.1) и (2.2) с учетом *⁾

(2.1^/)

(2.2^/)

Комплексные амплитуды падающей и отраженной волн напряжений и тока в любом сечении l описываются через амплитуды волн в некотором фиксированном сечении, например, l=0:

; (2.4)

; (2.5)

где - комплексные амплитуды падающей волны напряжения и падающей волны тока в сечении l=0;

- комплексные амплитуды отраженной волны напряжения и отраженной волны тока в сечении l=0.

Коэффициент распространения  для рассматриваемого типа волны комплексная величина и определен формулой . При выводе основных выражений, характеризующих режим в линиях конечной (короткой) длины, обычно применяют линии передачи с малыми потерями. Это дает возможность пренебречь затуханием (=0) и использовать для коэффициента отражения продольную постоянную распространения  ( - постоянная распространения в данной линии).

Тогда из (2.3) и (2.4) для коэффициента отражения в произвольном сечении получаем

(2.6)

 формула трансформации коэффициента отражения,

где - коэффициент отражения по напряжению в сечении l=0.

Коэффициент отражения в любом сечении приобретает разные значения. Например, если при смещении на расстояние фаза коэффициента отражения изменится на 360⁰, то значение коэффициента отражения в линии повторится. Если , то , через _В/4 фаза коэффициента отражения изменится на 180⁰.

Коэффициент отражения в общем случае комплексная величина

. (2.7)

С учетом этого равенства записываем (2.1^/)

(2.8)

Очевидно, что максимальное значение напряжения (пучность) получается при , где n=0, 1, 2…….т.е. в точках , так что

.

Минимальное значение (узел) напряжения будет при и равно

.

Отношение минимального значения полного напряжения (или тока, или напряженности поля) в линии к максимальному значению полного напряжения (или тока, или напряженности поля) в линии называется коэффициентом бегущей волны

=1/ . (2.9)

Часто вместо КБВ пользуются обратной ему величиной, называемой коэффициентом стоячей волны (КСВ) Введем обозначение для К_св- .

Следовательно, коэффициент К_бв будет обозначаться как 1/ .

= . (2.10)

Напряжение в линии, описываемое формулой (2.8), есть комплексная функция координаты l.

(2.11)

Для каждого значения Г₀ могут быть построены зависимости модуля напряжения в линии и его фазы (l).

Рассмотрим примеры.

1) Режим бегущей волны.

В этом случае: Г₀=0, отраженных волн нет (рис.2.3), как следует из (2.8) , где ; .

Д ля тока также имеем . Амплитуда напряжения и тока постоянна в любом сечении и фаза меняется по линейному закону.

Рис.2.3

На рис. 2.3. показаны амплитуды и фазы напряжения (непрерывная линия), тока (пунктирная линия) в режиме бегущей волны.

2. Режим холостого хода (х.х.).

; . В этом случае амплитуды падающей и отраженной волн напряжения одинаковы и фазы равны. Это может быть при разомкнутой на конце линии. Из (2.8)

,

.

На конце линии при l=0 получается минимальное значение тока (узел тока) и максимальное значение напряжения (пучность) (см. рис 2.4). Коэффициент отражения при разомкнутом отрезке линии длиной L равен:

. (2.12)

Практически в диапазоне СВЧ режим х.х. создать не удается. Действительно с электродинамической точки зрения на конце линии для этого режима следует потребовать выполнения . Такое граничное условие выполняется лишь на поверхности идеального магнитного проводникового материала, который может быть представлен лишь теоретически.

На рис. 2.4. изображены амплитуда и фаза напряжения и тока (непрерывная линия для напряжения и пунктирная линия для тока в обоих случаях) в режиме холостого хода.

3) Режим короткого замыкания (к.З.).

; - режим к.з.

В этом случае амплитуды падающей и отраженных волн одинаковы, а фазы отличаются на 180⁰. В сумме они дают нуль напряжения на конце линии (см. рис 2.5), что может быть при коротком замыкании, поэтому, этот режим носит название к.з.

Из (2.8) для этого режима получаем значения напряжения и тока

,

.

Условие к.з. соответствует случаю , т.е. для создания в линии к.з. на конце ее необходимо поставить идеальный электрический проводник (металл). На нем =0, откуда сразу видно, что Г₀=-1. В соответствии с (2.8) коэффициент отражения к.з. отрезка линии длиной L равен

. (2.13)

Н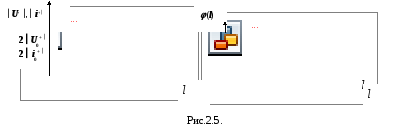 а рис. 2.5. изображены амплитуды и фазы напряжения непрерывная линия), тока (пунктирная линия) в режиме короткого замыкания

4) Режим смешанных волн.

В общем случае произвольной нагрузки модуль коэффициента отражения меняется в пределах от 0 до 1, а фаза от 0 до 360⁰. Если коэффициент отражения от нагрузки не равен 0 (в линии имеется отраженная волна), то такой режим называется режимом смешанных волн. Если модуль коэффициента отражения равен единице, то наблюдается режим стоячих волн. В режиме стоячих волн передачи электромагнитной энергии по линии передачи не происходит.

В заключение еще раз подчеркнем, что понятие коэффициента отражения имеет смысл для одного типа волны. В многоволновых волноводах для нагрузки необходимо введение для каждого типа волны своего коэффициента отражения (а значит, и К_бв, и К_св).

Входное сопротивление

Через I(l) и U(l) могут быть введены понятия полных (входных) сопротивлений и проводимости в данном сечении линии.

; , (2.14)

используя коэффициент отражения и уравнения (2.3) и (2.1^/, 2.2^/)

; (2.15)

или введем понятие нормированных сопротивлений и проводимостей

и ,

Z_В  это волновое сопротивление линии передачи

; . (2.16)

Можно выразить через Z(l) следующими соотношениями

(2.17)

Определим формулу, дающую связь между сопротивлением в некотором сечении линии и сопротивлением в произвольном сечении линии . Так что . После простых преобразований (2.15) и (2.7) получаем

(2.18)

или (2.18а)

 формула трансформации сопротивления.

(2.19)

 формула трансформации проводимости.

Рассмотрим несколько частных случаев для (2.18) и (2.19).

1. При или 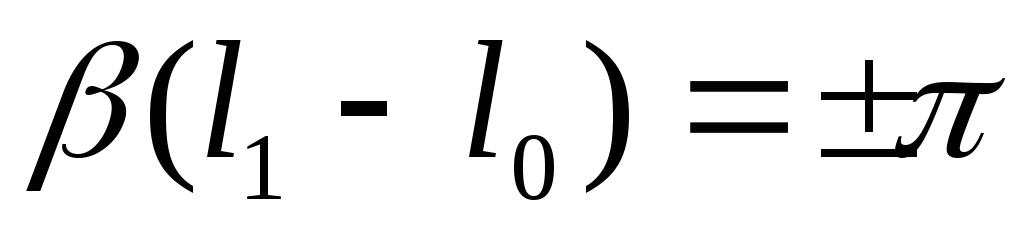получается

, (2.20)

т.е. через _В  сопротивление в линии повторяется.

2. При или получается

. (2.21)

Переходя к нормированным сопротивлениям и проводимостям, имеем:

. (2.22)

Т.е. нормированная проводимость в некотором сечении равна нормированному сопротивлению в сечении, отстаящем на _В .

3. При , получается , т.е. если в каком-либо сечении однородной линии сопротивление равно волновому, то и в любом другом сечении линии сопротивление является чисто активным и равным волновому. Нагрузка, сопротивление которой равно Z_В, называется согласованной.

4. При получается .

Если в каком-либо сечении однородной линии сопротивление равно нулю (здесь может быть короткое замыкание), то сопротивление в любом сечении линии является чисто реактивным, а вдоль линии оно меняется по закону тангенса.

3. При получается .

Если в каком-либо сечении однородной линии сопротивление равно бесконечности, то сопротивление в любом сечении чисто реактивное, а закон изменения его вдоль линии – котангенс.

3. Сопротивление узла напряжения (пучности тока) равно

(2.23)

. (2.24)