11

Kэ(θ,ϕ); γ (θ,ϕ); sgn Kэ(θ,ϕ) .

Эта зависимость чаще всего снимается экспериментально и строится в одной плоскости в прямоугольной системе координат.

Поляризация антенны имеет большое практическое значение, так как для полного приема сигнала требуется полное согласование поляризаций приемной и передающей антенн, а для подавления помехи - максимальное различие поляризационных параметров помехи и антенны. Знание поляризационных свойств антенны позволяет также оценить влияние РЛС на ЭМС в группировке.

1.1.2. Частотная характеристика антенны

Частотной характеристикой антенны (ЧХ) в общем случае называ-

ется зависимость амплитуды электромагнитного поля в дальней зоне в направлении главного максимума излучения от частоты передатчика.

Рассчитать напрямую эту зависимость часто бывает затруднительно, поэтому на практике частотные свойства антенн, как правило, оценивают косвенным образом по зависимости, например коэффициента стоячей волны

Для узкополосных антенн Кп≤1,1; для сверхширокополосных коэффициент достигает значения десятков единиц.

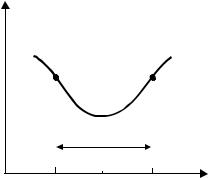
12 1.1.3. Ширина диаграммы направленности

Ширина ДН характеризует степень ее направленности (узость радиолуча). Ширина диаграммы направленности оценивается по ее главному лепестку и отсчитывается на некотором условном уровне относительно его максимума. Обычно ширина ДНА указывается для координатной плоскости (θ и ϕ)

и определяется как угол между на-

зуется 2θ0,5 p . Отметим, что уровень половинной мощности соответствует уровню 0,707 напряженности поля: так как Fp = F 2 , то 0,5Fp = (0,707F )2 .

1.1.4. Уровень паразитных лепестков

Уровень паразитных лепестков определяется как отношение их максимумов к главному максимуму. Обычно эту величину выражают в процентах или децибелах (дБ). Иногда ограничиваются указанием уровня только первого бокового лепестка, имеющего наибольшую величину. Наличие боковых и заднего лепестков крайне нежелательно, поскольку они бесполезно уносят энергию в ненужных направлениях, снижают ее концентрацию в главном лепестке, создают помехи другим станциям.

1.1.5. Максимальный коэффициент направленного действия

Коэффициентом направленного действия антенны в заданном направ-

лении называется число, показывающее, во сколько раз плотность ее потока в какой-либо точке пространства в этом направлении больше плотности потока мощности в той же точке для случая, когда антенна излучала бы ненаправленно (изотропно). Существуют и другие варианты определения КНД.

КНД обозначается буквой "D" и является функцией углов θ и ϕ:

13

где ПА и ПИ - плотность потока мощности в одной и той же точке для направленной и изотропной антенн; РА и РИ - мощность, подводимая к соответствующей антенне. Предполагается, что обе антенны являются идеальными излучателями, т.е. не имеют потерь.

КНД антенны определяется формой ее АДН:

∫ ∫F 2 (θ,ϕ)sinθ dϕ dθ

0 0

Обычно, когда говорят о КНД, имеют в виду его максимальное значение. Оно соответствует направлению максимума ДНА, где F (θ,ϕ) =1. При этом

∫ ∫F 2 (θ,ϕ)sinθ dϕ dθ

0 0

Сравнивая (1.9) и (1.10), можно записать:

Расчет Dmax по формуле (1.10) является достаточно трудоемким, поэтому для его ориентировочной оценки допускают, что в пределах главного лепестка F(θ,ϕ) =1, а за его пределами F(θ,ϕ) = 0. Поскольку размеры

главного лепестка определяются величинами 2θ0,5 p и 2ϕ0,5 p , выражение

(1.10) приводится к виду:

Если учесть, что часть мощности уходит в боковые лепестки, а также неравномерность излучения в пределах главного, то следует ввести коэффициент потерь kп, среднюю величину которого можно принять равным

0,6...0,7. Тогда