Вопросы для самопроверки и упражнения:

1. Доказать дистрибутивноть справа и слева операций пересечения и объединения относительно друг друга на системе множеств:

A(BC)=(AB)(AC) – дисрибутивность слева  относительно ;

A(BC)=(AB)(AC) – дисрибутивность слева  относительно ;

(AB)C=(AС)(AC) – дисрибутивность справа  относительно ;

(AB)C=(AС)(AC) – дисрибутивность справа  относительно ;

Проиллюстрировать на примере конкретных множеств, а также диаграммами Венна.

2. Пусть R₁, R₂ – бинарные отношения, определенные на множестве M={1, 2, 3, 4}. Показать на примере заданных ниже отношений R₁,R₂MM некоммутативность операции композиции отношений (составного отношения), т.е. R₁R₂R₂R₁, если:

а)R₁ – “быть меньше”, R₂ – “быть больше, по крайней мере на 2”;

б) R₁ – “быть больше”, R₂ – “иметь общий делитель, отличный от 1”;

3. Пусть операция  на множестве M={a, b, c} определена таблицей Кэли (рис. 3.4). Подтвердить ассоциативность и коммутативность операции .

4. Каковы свойства операций  и , заданные таблицами Кэли (рис. 3.5)?

3.4 Гомоморфизмы и изоморфизмы

Множество M вместе с заданным на нем операциями {₁, ₂, …,_m} называется алгеброй. Обозначение алгебры:

A=(M; ₁, ₂, …,_m),

где M называется основным множеством (несущим множеством, носителем), а ={₁, ₂, …,_m} – сигнатурой алгебры A .

Примером алгебры является полугруппа – множество M с заданной на нем одной бинарной ассоциативной операцией (обозначается:  ), т.е. A={M;  , например множество натуральных чисел N с операцией сложения + на нем, т.е. A={N; +} является полугруппой.

Типом алгебры A называется вектор арностей операций сигнатуры. Например, в алгебре A=где– множество действительных чисел, + и – соответственно операции сложения и умножения (такая алгебра называется полем действительных чисел), сигнатура ={+, } включает две бинарные операции – сложение и умножение. Поэтому тип данной алгебры (2, 2).

Множество M вместе с заданными на нем отношениями {R₁, R₂, …, R_n} называется моделью. Обозначим модели:

M =(M; R₁, R₂, …, R_n),

где M – несущее множество (универсум), ={R₁, R₂, …,R_n} – сигнатура модели M . Например, моделью M₁ является множество M₁ чисел с отношениями: “быть больше” (>) и “быть равным” (=), т.е. M₁=(M₁; >, =), или некоторое множество M₂ людей с отношением R – “быть руководителем”, т.е. M ₂=(M₂; R), и т.д.

Множество M вместе с заданными на нем операциями {₁, ₂, …,_m} и отношениями {R₁, R₂, …, R_n} называется алгебраической системой, или алгебраической структурой. Обозначение алгебраической структуры:

M=(M; ₁, ₂, …, _m, R₁, R₂, …, R_n).

Таким образом, алгебры – это алгебраические структуры с пустым множеством отношений. Другим частным случаем алгебраических структур являются модели, т.е. множества, на которых заданы только отношения.

Пусть между множествами A и B установлено соответствие Г – отображение A в B, т.е. Г: AB. Это означает, что каждому элементу а из A поставлен в соответствие Г единственный элемент  из B, т.е. Г(а)=. Пусть также на множестве A задана операция , на множестве B – операция , обе одинаковой арности, например обе бинарные, так что a  b=c, a,b,cA, и   =, ,,B. Таким образом, имеем две алгебры (A; ) и (B; y).

Тогда отображение Г: AB называется гомоморфизмом алгебры (A; ) в алгебру (B; y), если выполняется условие:

Г(a  b)=Г(а) y Г(b). (3.1)

Если при этом отображение Г: AB является взаимно однозначным соответствием, оно называется изоморфизмом алгебры (A; ) на алгеб-ру (B; y). В этом случае существует обратное отображение Г^–1: BA, также взаимно однозначное:

Г^–1(  )=Г^–1()  Г^–1().

Отображение Г^–1 – это, в свою очередь, изоморфизм B на A. Итак, если существует изоморфизм A на B, то существует изоморфизм B на A. При этом алгебры (A; ) и (B; y) называются изоморфными.

В более общем случае, если на множествах A и B заданы несколько операций соответственно (A; ₁, ₂, …, _m) и (B; ₁, ₂, …, _m), отображение Г: AB является гомоморфизмом алгебры (A; ₁, ₂, …, _m) в алгебру (B; ₁, ₂, …, _m), если условия, аналогичные (3.1), выполняется для каждой пары операций ₁ и ₁, …, _m и _m.

В силу взаимной однозначности соответствия Г: AB при изо-морфизме мощности основных множеств изоморфных алгебр равны. Поэтому проверка алгебр на изоморфизм сводится к проверке условия гомоморфизма для каждой пары операций и установления взаимной однозначности соответствия Г (равной мощности множеств A и B).

Аналогично определяется гомоморфизм (изоморфизм) множеств с отношениями – моделей (A; R₁, R₂, …, R_n) и (B; R₁, R₂, …, R_n).

Пусть, например, на множестве A задано бинарное отношение R(a, b), a,bA, и на множестве B – бинарное отношение R(, ), ,B. Тогда отображение Г: AB является гомоморфизмом модели (A; R) в модель (B; R), если для любой пары элементов a, b из А такой, что a и b находятся в отношении R, следует, что их отображения Г(а)= и Г(b)= находятся в отношении R (см. рис 3.6), т.е.

a R b влечет Г(а) R Г(b) для любых a,bA. (3.2)

Если при этом отображение Г: AB является взаимно однозначным соответствием, оно называется изоморфизмом модели (A; R) на модель (B; R). В этом случае существует и обратное отображение Г^–1: BA, также являющееся изоморфизмом:

 R  влечет Г^–1() R Г^–1() для любых ,B.

При этом модели (A; R) и (B; R) называются изоморфными.

Важным примером изоморфных алгебр являются так называемые булевы алгебры, в том числе:

1) ((U); , , –) – булева алгебра множеств;

Здесь ((U) – множество всех подмножеств (булеан) множества U;

{, , –} – соответственно операции пересечения, объединения, дополнения над множествами;

2) (B_n; , , –) – булева алгебра двоичных векторов длины n.

Здесь B_n – множество всех двоичных векторов длины n, т.е.

B_n=BB…B=Bⁿ, где B={0, 1};

{, , –} – операции логического (покомпонентного) умножения, сложения и дополнения соответственно, определенные следующим образом:

для любых векторов =(₁, ₂, …, _n) и =(₁, ₂, …, _n):

а) =(₁₁, ₂₂, …, _n_n), при этом =1, если==1, и=0 – в любом другом случае, т.е.

б) =(₁₁, ₂₂, …, _n_n), при этом =0, если==0, и=1 – в любом другом случае, т.е.

в)

где

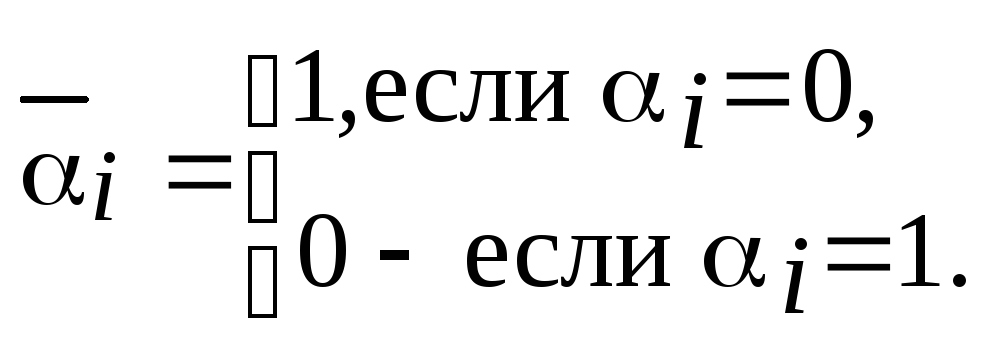
Изоморфизм булевых алгебр широко используется в компьютерных вычислениях, например, при необходимости выполнения операций над множествами с применением соответствующих и легко реализуемых на компьютере поразрядных операций над соответствующими двоич-ными векторами.

Пример 1. Пусть M₁ – множество сотрудников организации и R₁ – заданное на нем отношение “быть старше” ();M₂ – конечное множество натуральных чисел (ограниченное, например, числом 100) и R₂ – заданное на нем отношение “быть больше” (>). Гомоморфны (изоморфны) ли модели:

A=(M₁; ) иB=(M₂; >)?

1. Определим отображение Г: M₁M₂ следующим образом: каждому сотруднику организации из M₁ поставим в соответствие Г число из M₂, соответствующим его возрасту (в годах). Установленное таким образом отображение Г: M₁M₂ является гомоморфизмом моделей A=(M₁; ) иB=(M₂; >), так как очевидно выполняется условие (3.2). Действительно, если ‘Иванов’, 37 лет, старше ‘Петрова’, 26 лет, т.е.

‘Иванов’ ‘Петрова’ и Г(‘Иванов’)=37,

Г(‘Петров’)=26, то и 37>26.

2. Однако установленное отображение Г: M₁M₂ не является изоморфизмом моделей A=(M₁; ) иB=(M₂; >), так как не является в общем случае взаимно однозначным (если в организации имеются сотрудники одного возраста, например ‘Петров’ 26 лет и ‘Сидоров’ 26 лет. В этом случае обратное соответствие Г^–1 не является отображением, поскольку не функционально (отсутствует единственность образа 26 на множество сотрудников организации).

Таким образом, заданные модели A=(M₁; ) иB=(M₂; >) гомоморфны, но не изоморфны.

Пример 2. Пусть Z_n – множество всех целых чисел, Z_2n – множество всех четных целых чисел. Изоморфны ли следующие алгебры:

а) A=(Z_n;+) и B=(Z_2n; +) при отображении Г: n2n,

б) A=(Z_n;+) и B=(Z_n; +) при отображении Г: n(–n),

в) A=(Z_n; ) и B=(Z_n; ) при отображении Г: n(–n),

г) A=(Z_n; ) и B=(Z_2n; ) при отображении Г: n2n,

д) A=(Z_n; +, ) и B=(Z_2n; +, ) при отображении Г: n2n,

где +,  – операции арифметического сложения и умножения соответственно.

а) Условие гомоморфизма для алгебр A=(Z_n;+) и B=(Z_2n; +) проиллюстрировано на рис. 3.7, где изображены два множества Z_n, Z_2n и в Z_n выделены произвольные два элемента a, b.

В соответствии с ле-вой частью условия (3.1) гомоморфизма для бинар-ных операций выполним над a и b операцию сложения + алгебры A и отобразим результат с=a+b в множестве Z_2n алгебры B. При задан-ном отображении Г: n2n элементу с мно-жества Z_n соответствует элемент 2с множества Z_2n, т.е. левая часть условия (3.1) примет вид:

Г(a+b)=2(a+b).

Правая часть условия (3.1) требует сначала отображения элементов a, b в множество Z_2n (получаем Г(а)=2а, Г(b)=2b), а затем осуществления над их отображениями операции сложения (+) алгебры B , т.е. правая часть условия (3.1) примет вид:

Г(а)+Г(b)=2a+2b.

Таким образом, условие гомоморфизма (3.1) для алгебр A=(Z_n;+) и B=(Z_2n; +) при отображении Г: n2n имеет вид:

Г(a+b)=Г(а)+Г(b), т.е.

2(a+b)=2a+2b.

Так как данное условие выполняется, алгебры A и B гомо- морфны, а в силу взаимной однозначности отображения Г: n2n они и изоморфны.

б) Отображение Г: n(–n) для алгебр A=(Z_n;+) и B=(Z_n; +) является изоморфизмом. Действительно, условие (3.1) имеет вид:

–(a+b)=(–a)+(–b)

и, кроме того, отображение Г: n(–n) (каждому целому числу n в алгебре A соответствует то же целое число, но с противоположным знаком (–n) в алгебре B ) – взаимно однозначно.

в) Отображение Г: n(–n) для алгебр A=(Z_n; ) и B=(Z_n; ) не является ни изоморфизмом, ни гомоморфизмом, так как не выполняется условие (3.1) гомоморфизма:

– (ab)(–a)  (–b).

г) Алгебры A=(Z_n; ) и B=(Z_2n; ) не являются гомоморфными, а значит, и изоморфными при отображении Г: n2n, поскольку для них не выполняется условие гомоморфизма (3.1):

2(ab) 2a2b.

д) Для алгебр A=(Z_n; +, ) и B=(Z_2n; +, ) при отображении Г: n2n условие гомоморфизма выполняется для операций сложения и не выполняется для операций умножения [см. а) и г)], поэтому алгебры A и B не являются гомоморфными.

Пример 3. Гомоморфны (изоморфны) ли алгебры ипри отображении Г:aloga множества действительных и положительных чисел соответственно)?

Алгебры иизоморфны при заданном отображении Г:alog a, так как выполняется условие (3.1):

log (ab)=log a + log b

и отображение Г: aloga взаимно однозначно. В частности, этот принцип (изоморфизм указанных алгебр при данном отображении) используется при вычислениях с помощью логарифмической линейки.

Пример 4. Изоморфны ли булевы алгебры множеств ((U); , , –) и ((U); , , –), образованные двумя различными множествами U и U одинаковой мощности?

Алгебры ((U); , , –) и ((U); , , –), где |U|=|U|, изоморфны, так как операции у них просто одинаковы, а отображением Г может служить любое взаимно однозначное соответствие между U и U. Например, множества U={1, 2, 3} и U={a, b, c} одинаковой мощности, |U|=|U|=3. Тогда отображение Г: {1a, 2b, 3c} задает изоморфизм алгебр ((U); , , –) и ((U); , , –).

Пример 5. Пусть алгебры A=(N; +) и B=(N₃; ), где  – сложение по модулю 3 и N₃={0, 1, 2}, и отображение Г: NN₃ определено следующим образом: Г(n) равно остатку от деления n на 3. Иначе говоря,

Если n=3a+b, где b<3, то Г(n)=b.

Например, 21=0, 22=1 и т.д.

Гомоморфны (изоморфны) ли алгебры A=(N; +) и B=(N₃; )?

Пусть n₁=3a₁+b₁ и n₂=3a₂+b₂ – два произвольных натуральных числа из N; b₁, b₂<3. Проверим условие (3.1):

Г(n₁+n₂)=Г(n₁)  Г(n₂),

Г(3a₁+b₁+3a₂+b₂)=Г(3a₁+b₁)  Г(3a₂+b₂),

Г(b₁+b₂)=Г(b₁)  Г(b₂),

Г(b₁+b₂)=b₁b₂.

Очевидно это условие выполняется. Например, пусть n₁=56, n₂=37. Тогда 56=318+2, 37=312+1; подставив в полученное условие гомо-морфизма, убедимся в его выполнимости:

Г(2+1)=21,

0=0.

Таким образом, отображение Г – гомоморфизм. Но оно не является изоморфизмом, так как нет взаимной однозначности для Г: NN₃.

Этот пример показывает, что возможен гомоморфизм бесконечной алгебры (т.е. алгебры с бесконечным основным множеством) в конеч-ную алгебру.

Пример 6. Изоморфны ли модели ((U); ) и (B₃; ), где:

(U) – множество всех подмножеств (булеан) множества U={a, b, c};

B₃ – множество всех двоичных векторов длины 3;

 – отношение нестрогого включения;

 – отношение нестрогого порядка над векторами такое, что для двух двоичных векторов =(₁, ₂, ₃) и =(₁, ₂, ₃);

, т.е. (₁, ₂, ₃)(₁, ₂, ₃);

если и только если ₁₁, ₂₂, ₃₃.

Например, (100)(101), но (101) и (011) несравнимы.

(U)={, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}};

B₃={(000), (001), (010), (011), (100), (101), (110), (111)} (для упроще-ния обозначений запятые между компонентами векторов опущены).

Мощности этих множеств равны: |(U)|=|B₃|=8. Отображение Г: (U)B₃ является взаимно однозначным (см. также пример 4 из параграфа 3.1):

Г: (000), {a}(100), {b}(010), …, {a, c}(101), …, {a, b, c}(111).

Остается показать, что условие гомоморфизма (3.2) выполняется для заданных отношений:

АB влечет Г(А)Г(B) для любых А,В(U); A,BU.

Смысл этого условия заключатся в следующем. Если два множества A, B из (U) сравнимы по отношению включения  , то соответст-вующие им векторы  и  из B₃ такие, что Г(А)= и Г(В)=, сравнимы по отношению неравенства  и из того, что АВ, следует, что .

Очевидно, что данное условие выполняется. Например, из того, что {a}{a, c} следует (100)(101). А в силу взаимной однозначности отображения Г справедливо и обратное, например из того, что (010)(111), следует, что {b}{a, b, c}:

 влечет Г^–1() Г^–1() для любых ,B₃.

Таким образом, установленное отображение Г: (U)B₃ является изоморфизмом; модели ((U);  ) и (B₃;  ) изоморфны. Отметим, что изоморфными будут и другие аналогичные модели ((U);  ) и (B_n;  ), если мощность несущего множества |U| и длина векторов n из B_n равны, т.е. |U|=n. В этом случае выполняется взаимно однозначное соответствие

Г: (U)B_n , |(U)|=|B_n|.

Пример 7. Используя установленное в предыдущем примере взаимно однозначное соответствие между множествами из (U), где U={a, b, c}, и двоичными векторами длины 3 и B₃, проиллюстрировать на примере конкретных множеств А={a, c} и B={b, c}, A,BU, изоморфизм между булевыми алгебрами множеств ((U); , , –), |U|=3, и двоичных векторов длины 3 (B₃; , , –).

Для U={a, b, c}:

(U)={, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

При n=3 |(U)|=|B₃|=8:

B₃={(000), (001), (010), (011), (100), (101), (110), (111)}.

Установленное в примере 6 взаимно однозначное соответствие Г: (U)B₃ для заданных множеств А={a, c} и B={b, c} имеет вид:

1) Г(А)=Г({a, c})=(101)=, Г(В)=Г({b, c})=(011)= и наоборот

Г^–1()=Г^–1((101))={a, c}; Г^–1()=Г^–1((011))={b, c}.

2) Подтвердим теперь выполнение условия гомоморфизма для каждой пары операций булевых алгебр на примере множеств A,BU:

а) Г(АВ)=Г({a, c}{b, c})=Г({c})=(001)=(101)(011)=;

б) Г(АВ)=Г({a, c}{b, c})=Г({a, b, c})=(111)=(101)(011)=;

в)Г(U\A)=Г({a, b, c}\{a, c})=Г({b})=(010)=.

Таким образом, для трех пар булевых операций имеет место выполнение условия гомоморфизма:

а) Г(АВ)=;

б) Г(АВ)=;

в) .

Алгебры ((U); , , –) и (B₃; , , –) гомоморфны, и отображение множеств Г: (U)B₃ взаимно однозначно. Следовательно, данные алгебры также и изоморфны при данном отображении.