
- •Н.И. Калядин
- •Н.И. Калядин
- •Глава 1. Функции алгебры логики
- •1.1. Основные определения
- •Геометрическое представление фал.
- •2.3 Задачи и упражнения iiIго типа *.
- •1.4 Свойства конъюнкции, дизъюнкции и отрицания.
- •1.5 Свойства сложения по модулю два, импликации и функции Шеффера и Вебба.
- •Алгоритм приведения формулы к днф.
- •Совершенные дизъюнктивные и конъюнктивные нормальные формы.
- •Алгоритм построения скнф.
- •Алгоритм нахождения сднф путем тождественных преобразований
- •Совершенно полиноминальная нормальная форма (спнф).
- •Алгоритм построения спнф.
- •Глава 2. Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры логики.
- •2.1 Задачи и упражнения iго – типа *.
- •1.8 Методы определения линейности фал.
- •1. Использование таблиц истинности.
- •Замечательное свойство классов фал (классов Поста):
- •1.9 Функционально замкнутые классы. Критерий полноты *.
- •2. Использование полинома Жегалкина.
- •1.7 Основные классы функций алгебры логики
- •Алгоритм построения сднф.
- •2.2 Задачи и упражнения iiго – типа *.
- •1.6 Аналитические формы представления фал. Дизъюнктивные и конъюнктивные нормальные формы
- •1.3 Выражение одних элементарных функций через другие
- •1.2 Элементарные функции алгебры логики
- •Предисловие.
- •Список литературы.
Совершенные дизъюнктивные и конъюнктивные нормальные формы.
Л
11
 =p/z
=p/z y
y x
x p
p ¬z
¬z y
y z
z x,
x, =y
=y z
z p
p ¬x
¬x y/z
y/z p
p x
x y,
y, =z/x
=z/x ¬(y
¬(y p
p (x
(x y
y z))
z)) x
x p,
p, =x
=x y
y z
z p
p x
x y
y x/z
x/z ¬y
¬y p,
p, =x/z
=x/z p
p x
x p
p x
x ¬z
¬z p
p y,
y,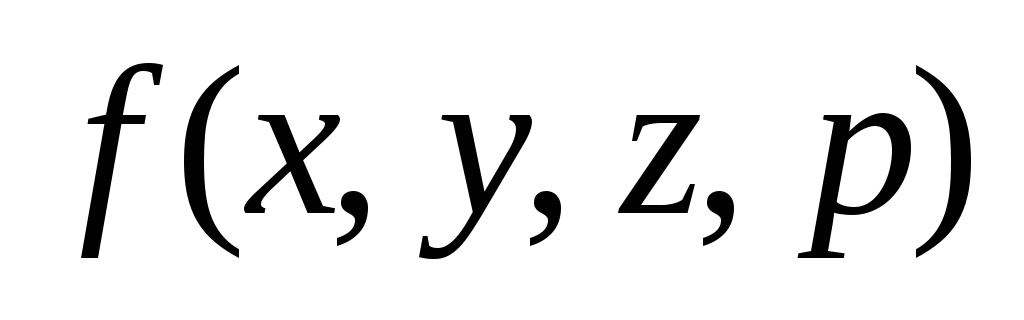 =x
=x z
z y
y ¬p
¬p x
x y
y z
z p/x
p/x z,
z, =y/p
=y/p x
x y
y ¬p
¬p z
z x
x z
z x,
x,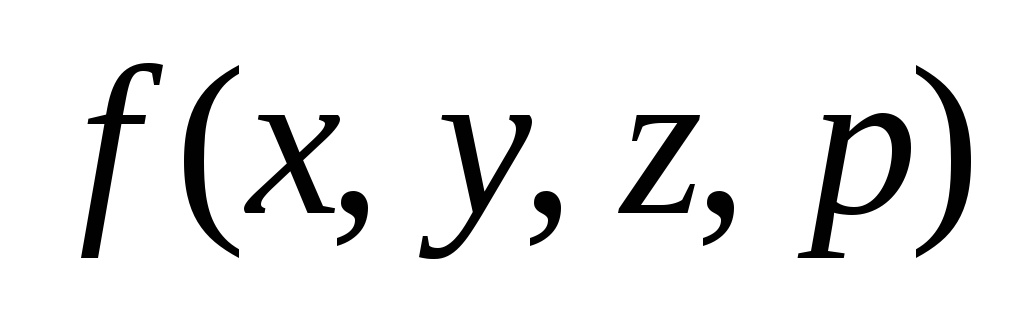 =p
=p ¬y
¬y x
x z
z p
p y/z
y/z x
x p,
p, =p
=p z
z ¬(y
¬(y x
x z)
z) p/x
p/x z
z y
y x,
x, =x
=x y
y z
z x
x ¬(y
¬(y z)
z) y
y p/x,
p/x, =z/x
=z/x p
p y
y x
x y
y z
z ¬x
¬x p,
p,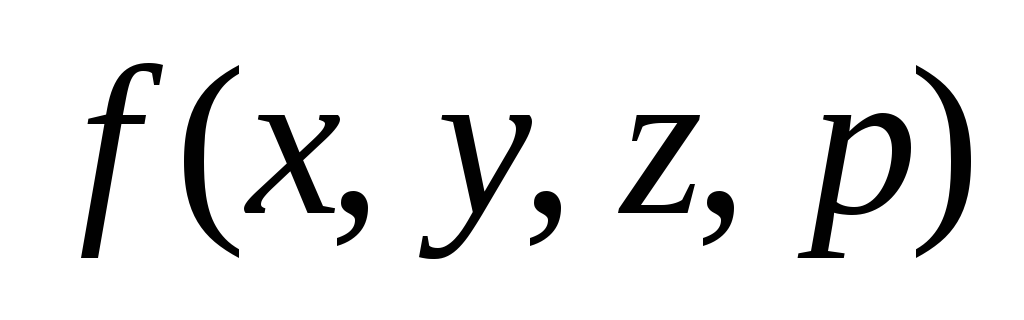 =y
=y x
x z
z ¬p
¬p y
y x
x y
y z/x,
z/x, =z
=z y
y x/y
x/y z
z x
x y
y ¬z
¬z p,
p, =x
=x ¬y
¬y z
z x
x p
p y/z
y/z x
x y,
y, =x
=x y
y z
z p
p x
x y/x
y/x ¬z
¬z y,
y, =p
=p x
x y/z
y/z p
p y
y x
x z
z ¬y
¬y p,
p, =x
=x ¬z
¬z p/z
p/z x
x y
y z
z p
p p
p y,
y, =z
=z p
p ¬x
¬x p
p y
y x/z
x/z y
y z,
z, =x
=x y
y z
z x/y
x/y z
z p
p z
z ¬x,
¬x, =x
=x y
y ¬p/y
¬p/y z
z y
y z
z p
p x,
x, =z
=z ¬p
¬p z/y
z/y x/z
x/z p
p y
y x,
x, =p
=p y
y z
z p
p y/¬x
y/¬x y
y p
p y,
y,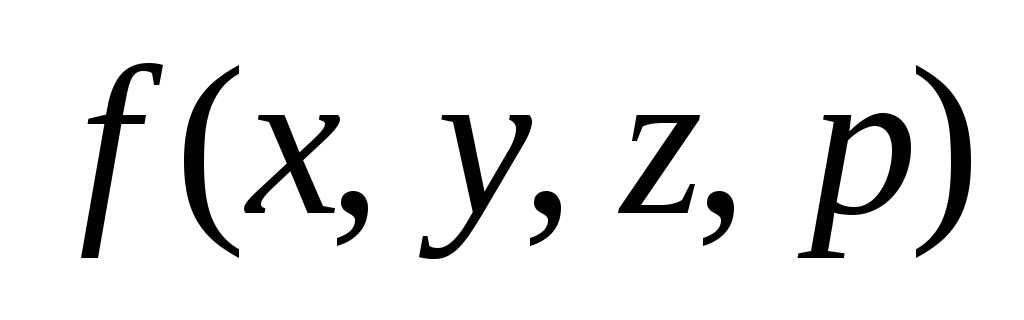 =p/y
=p/y z
z p
p x
x z
z y
y x
x ¬z
¬z y,
y, =z
=z ¬p/x
¬p/x z
z y
y p
p y
y x
x z,
z, =y
=y x/z
x/z ¬p
¬p x
x y
y z
z x
x p,
p, =p
=p x
x z/p
z/p x
x y
y ¬z
¬z p
p y,
y, =p
=p z
z x
x y
y ¬y/p
¬y/p z
z x
x p,
p, =x
=x y
y z
z p
p z
z ¬x/y
¬x/y p
p z,
z,
28
=z y
y p
p z
z y
y ¬p/x
¬p/x y
y z,
z,
 .
.
А налогично
для булевой функции
налогично
для булевой функции![]() получаем
её представление в виде совершенной
КНФ:
получаем
её представление в виде совершенной
КНФ:

Приведенные теоремы позволяют сформулировать следующую теорему:
Теорема 6 (о
функциональной полноте).
Для любой
булевой функции
![]() найдется
формула
найдется
формула![]() ,
представляющая функцию
,
представляющая функцию![]() .
.
Е сли
сли![]() ,
то существует представляющая ее формула
,
то существует представляющая ее формула![]() ,
находящаяся в СДНФ:
,
находящаяся в СДНФ:
![]()
и такое представление единственно с
точностью до порядка следования
конституент единицы. Если
такое представление единственно с
точностью до порядка следования
конституент единицы. Если![]() ,
то существует представляющая ее формула
,
то существует представляющая ее формула![]() ,
находящаяся в СКНФ:
,
находящаяся в СКНФ:
![]()
и такое представление единственно с точностью до порядка следования конституент нуля.
Указанная теорема
дает возможность сформулировать алгоритм
перехода от табличного задания функции
![]() к
ее представлению в виде СДНФ(СКНФ).
к
ее представлению в виде СДНФ(СКНФ).
Алгоритм построения скнф.
1. Выбрать в таблице
задания функции все наборы аргументов
(![]() ),
на которых
),
на которых
![]() .
.
2. Выписать
конституенты нуля
![]() ,
соответствующие этим наборам. При этом,
если аргумент
,
соответствующие этим наборам. При этом,
если аргумент![]() входит в данный набор как 0, то он
вписывается без изменений в дизъюнкт,
соответствующий данному набору. Если
входит в данный набор как 0, то он
вписывается без изменений в дизъюнкт,
соответствующий данному набору. Если![]() входит в данный набор как 1, то в
соответствующий дизъюнкт вписывается
его отрицание (
входит в данный набор как 1, то в
соответствующий дизъюнкт вписывается
его отрицание (![]() ).
).
3
13
28. Доказать теорему: при суперпозиции монотонных функций вновь получаются монотонные функции.
29. Функция называется
сохраняющей
константу
![]() ,
если на наборе аргументов вида
,
если на наборе аргументов вида![]() она принимает значение
она принимает значение![]() .
Доказать, что суперпозиция функций,
сохраняющей константу
.
Доказать, что суперпозиция функций,
сохраняющей константу![]() ,
вновь является функцией, сохраняющей
эту константу.
,
вновь является функцией, сохраняющей
эту константу.
30. Если функции
![]() и
и![]() самодвойственны, то самодвойственны
ли функции
самодвойственны, то самодвойственны
ли функции![]() и
и![]() ?
?
31. Если функции
![]() и
и![]() линейны, то линейны ли функции
линейны, то линейны ли функции![]() ?
?
32. Булева функция называется симметричной, если она не изменяется при любом переименовании аргументов.
Фундаментальной
симметричной булевой функцией
индекса
![]() называется
такая симметричная булева функция, у
которой все конъюнкции, входящие в
совершенную ДНФ этой функции, имеют
ровно
называется
такая симметричная булева функция, у
которой все конъюнкции, входящие в
совершенную ДНФ этой функции, имеют
ровно
![]() букв без отрицания.
букв без отрицания.
Доказать следующую теорему: любая симметричная булева функция есть дизъюнкция фундаментальных булевых функций, индексы которых однозначно определяются представляемой симметричной функцией.
33. Определить число
самодвойственных функций, зависящих
от
![]() аргументов.
аргументов.
34. Доказать полноту системы булевой функции, состоящей из дизъюнкции, константы 0 и эквивалентности. Образует ли эта система базис?
35. Образует ли базис система булевых функций, состоящая из импликации и константы 0?
.36. Установить, является ли полной система, состоящая из дизъюнкции, импликации и конъюнкции.
37. Образуют ли
полную систему функция
![]() и отрицание?
и отрицание?
38. Доказать, что если некоторая булева функция не сохраняет константы и несамодвойственна, то она немотонна и нелинейна.
39. Записать основные законы алгебры Буля при арифметической интерпретации следующих логических операций:
![]()
где “·”, ”+”, “-“ – арифметические операции умножения, сложения и вычитания соответственно.
26
