
- •Н.И. Калядин
- •Н.И. Калядин
- •Глава 1. Функции алгебры логики
- •1.1. Основные определения
- •Геометрическое представление фал.
- •2.3 Задачи и упражнения iiIго типа *.
- •1.4 Свойства конъюнкции, дизъюнкции и отрицания.
- •1.5 Свойства сложения по модулю два, импликации и функции Шеффера и Вебба.
- •Алгоритм приведения формулы к днф.
- •Совершенные дизъюнктивные и конъюнктивные нормальные формы.
- •Алгоритм построения скнф.
- •Алгоритм нахождения сднф путем тождественных преобразований
- •Совершенно полиноминальная нормальная форма (спнф).
- •Алгоритм построения спнф.
- •Глава 2. Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры логики.
- •2.1 Задачи и упражнения iго – типа *.
- •1.8 Методы определения линейности фал.
- •1. Использование таблиц истинности.
- •Замечательное свойство классов фал (классов Поста):
- •1.9 Функционально замкнутые классы. Критерий полноты *.
- •2. Использование полинома Жегалкина.
- •1.7 Основные классы функций алгебры логики
- •Алгоритм построения сднф.
- •2.2 Задачи и упражнения iiго – типа *.
- •1.6 Аналитические формы представления фал. Дизъюнктивные и конъюнктивные нормальные формы
- •1.3 Выражение одних элементарных функций через другие
- •1.2 Элементарные функции алгебры логики
- •Предисловие.
- •Список литературы.
2.3 Задачи и упражнения iiIго типа *.
1. Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
(a
 (
(
 b))
b)) ((
((
 (
(
 d))
d)) c))
c))

 (a
(a (b
(b
 )),
)),((a
 c)
c) (a
(a d))
d)) (((c
(((c (c
(c b))
b))
 )
)
 ),
),(

 d)
d) ((
((
 c)
c) (a
(a c)
c) (
(

 )
) (a
(a
 ))
)) (b
(b d),
d),(a

 )
) (
(

 )
) (
(
 c)
c) (
(
 b)
b) (b
(b c),
c),(a

 )
) ((b
((b
 )
) (
(

 )
) (d
(d b)
b) (
(
 d))
d)) (a
(a
 ),
),((


 )
) (a
(a b))
b)) (d
(d
 )
) (((
(((

 )
) c)
c) (a
(a b)),
b)),(a

 )
) (
(

 )
) (b
(b c)
c) (
(
 b)
b) (c
(c
 ),
),((a
 (c
(c (b
(b c)))
c)))

 (c
(c
 ))
)) (c
(c (
(

 )
) d),
d),((a

 )
) (
(

 )
) (
(

 )
) (
(
 d))
d)) ((
((
 c)
c) (c
(c d)),
d)),(a

 )
) ((
((
 d)
d) (b
(b d)
d) (
(

 )
) (b
(b
 ))
)) (a
(a c),
c),((d

 )
) (
(

 )
) (c
(c
 ))
)) ((
((
 b)
b) (c
(c b))
b)) (
(
 a),
a),((


 )
) (b
(b c))
c)) (
(

 )
) (((
(((

 )
) d)
d) (c
(c b)),
b)),((a
 b)
b) (
(
 c
c d)
d) (
(


 c
c d)
d)



 d,
d,((a
 b)
b) (a
(a
 ))
)) ((
((
 b)
b) (c
(c
 )
) (
(

 )
) (d
(d c)),
c)),((

 c)
c) (
(
 d)
d)
 )
) (
(
 b
b

 d)
d)

 a,
a,((b
 c)
c) (d
(d (
(

 ))
)) (
(

 )
) ((c
((c b)
b) (
(

 )),
)),(b
 d)
d) ((c
((c
 )
) (a
(a c)
c) (
(

 )
) (a
(a
 ))
)) (
(
 d),
d),((

 d)
d) (d
(d a))
a)) ((b
((b
 )
) (
(

 )
) (
(

 )
) (
(
 a)),
a)),(a

 )
) (((
(((

 )
) d)
d) (c
(c b))
b)) ((
((

 )
) (c
(c b)),
b)),(((d
 (d
(d c))
c))
 )
)
 )
) ((b
((b d)
d) (b
(b a)),
a)),((

 (
(
 a))
a)) d))
d))

 (b
(b (c
(c
 ))
)) (b
(b (
(
 c)),
c)),((c

 )
) (
(

 )
) (a
(a c)
c) (
(
 a))
a)) (b
(b
 )
) (b
(b d),
d),(d
 (
(

 )
) a)
a) ((b
((b (d
(d (d
(d c)))
c)))

 (d
(d
 ),
),(


 )
) (d
(d c)
c) (
(
 c)
c) (d
(d
 )
) (b
(b
 ).
).
1.4 Свойства конъюнкции, дизъюнкции и отрицания.
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Для этих функций имеют место следующие законы:
1)сочетательный
![]() ;
;
![]() ;
;
2)переместительный
![]() ;
;
![]()
3)распределительный
![]() ;
;
![]()
Рассмотрим теперь ряд простых, но весьма важных соотношений:

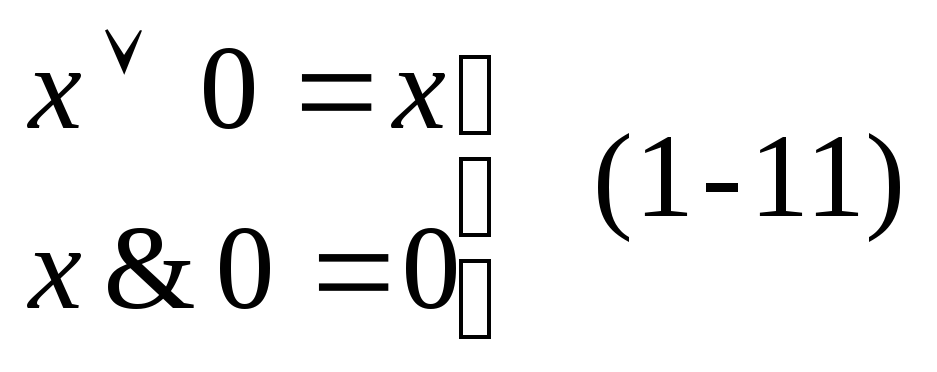


Как обобщение из формул (1 – 8) и (1 – 9) получаем следующие формулы, обычно называемые формулами де Моргана:
![]() (1
– 14)
(1
– 14)
![]() (1
– 15)
(1
– 15)
1.5 Свойства сложения по модулю два, импликации и функции Шеффера и Вебба.
Свойства функции сложения по модулю два и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств.

![]() (1 – 16)
(1 – 16)
Имеют место также очевидные соотношения:


 (1 – 17)
(1 – 17)
В отличие от всех ранее рассмотренных функций для импликации не имеют места переместительный и сочетательный законы:
32
9

 (1 – 18)
(1 – 18)
 =x
=x y
y p
p ¬z
¬z x/y
x/y z
z p
p x,
x, =y
=y x
x z
z p/¬x
p/¬x y
y z
z p
p x,
x, =p
=p y
y z
z x
x y/¬z
y/¬z p
p x
x y,
y, =x
=x y
y z/p
z/p x
x ¬z
¬z y
y p
p x,
x,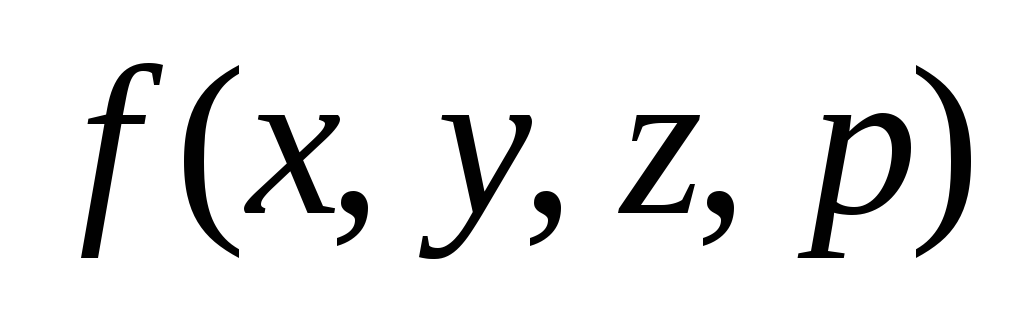 =z
=z p
p y
y p
p x/z
x/z p
p ¬y
¬y x,
x, =x
=x ¬y
¬y z
z p/x
p/x z
z y
y p
p x,
x, =y
=y p
p ¬z
¬z x
x y
y p/x
p/x y
y z,
z, =x/y
=x/y z
z p
p x
x z
z p
p y
y ¬z,
¬z, =p
=p z
z y
y x
x y
y z
z p
p x/¬y,
x/¬y, =x
=x y
y z
z p
p ¬x
¬x y
y x
x z/p,
z/p, =y
=y p
p z
z x
x ¬y
¬y z/p
z/p y
y x,
x, =¬p
=¬p z/x
z/x y
y z
z p
p x
x y
y p,
p, =p
=p ¬z
¬z y
y x
x y
y z/p
z/p x
x z,
z, =¬x
=¬x z
z p
p p
p y
y z/p
z/p z
z y,
y, =p
=p x
x z/y
z/y x
x p
p ¬z
¬z y
y p,
p, =z
=z x
x y
y ¬p
¬p x
x z/x
z/x y
y z,
z, =x/p
=x/p y
y z
z x
x y
y z
z p
p ¬x,
¬x, =y
=y p/x
p/x x
x z
z p
p y
y p
p ¬z,
¬z, =z
=z ¬y
¬y x/p
x/p z
z p
p x
x y
y z,
z, =p
=p ¬y
¬y z
z x
x z/p
z/p y
y x
x y,
y, =x
=x y
y z/p
z/p x
x y
y z
z p
p ¬x,
¬x, =z
=z p
p x
x y
y x/z
x/z y
y ¬p
¬p x,
x, =y
=y p
p x/z
x/z ¬y
¬y x
x y
y p
p z,
z, =x
=x y
y p
p ¬z
¬z x
x y
y z/p
z/p y,
y, =¬z
=¬z p
p x
x y
y x/y
x/y z
z p
p z,
z, =x
=x y
y p
p z
z y
y ¬x/y
¬x/y p
p z,
z, =z
=z p
p ¬y
¬y z/y
z/y x
x y
y p
p z,
z, =x
=x y
y z
z ¬p
¬p x/y
x/y x
x z
z p,
p,
30
=z p
p y
y z
z p
p x
x y/z
y/z ¬x,
¬x,
Пример 1-4.
Формулы:
![]() и
и![]() - дизъюнкты. Формулы
- дизъюнкты. Формулы![]() и
и![]() -
конъюнкты, а
-
конъюнкты, а![]() одновременно является и дизъюнктом, и
конъюнктом.
одновременно является и дизъюнктом, и
конъюнктом.
Дизъюнкция конъюнктов называется дизъюнктивной нормальной формой (ДНФ); конъюнкция дизъюнктов называется конъюнктивной нормальной формой (КНФ).
Пример 1-5.
Формула
![]() - ДНФ, формула
- ДНФ, формула![]() - КНФ, а формула
- КНФ, а формула![]() является одновременно КНФ и ДНФ.
является одновременно КНФ и ДНФ.
Теорема 3. 1. Любая формула эквивалента некоторой ДНФ.
2. Любая формула эквивалента некоторой КНФ.
Алгоритм приведения формулы к днф.
1. Выражаем все
логические операции, участвующие в
построении формулы, через {![]() &},
используя вышеприведенные эквивалентности.
&},
используя вышеприведенные эквивалентности.
2. Используя законы
де Моргана, переносим все отрицания к
переменным и сокращаем двойные отрицания
по правилу:
![]() .
.
3. Используя закон
дистрибутивности
![]() ,
преобразуем формулу так, чтобы все
конъюнкции выполнялись раньше дизъюнкций.
,
преобразуем формулу так, чтобы все
конъюнкции выполнялись раньше дизъюнкций.
Пример 1-6.
Привести к ДНФ формулу
![]() .
.
![]() .
.
Приведение формул к КНФ производиться аналогично приведению её к ДНФ, только вместо п. 3. применяется пункт:
:3’.
Используя закон дистрибутивности:
![]() преобразует формулу так, чтобы все
дизъюнкции выполнялись, раньше конъюнкции.
преобразует формулу так, чтобы все
дизъюнкции выполнялись, раньше конъюнкции.
Пример 1-7.
Приведем к КНФ формулу
![]()
![]()
![]() ,
являющейся КНФ.
,
являющейся КНФ.
