- •Н.И. Калядин
- •Н.И. Калядин
- •Глава 1. Функции алгебры логики
- •1.1. Основные определения
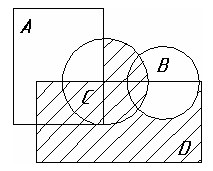
- •Геометрическое представление фал.
- •2.3 Задачи и упражнения iiIго типа *.
- •1.4 Свойства конъюнкции, дизъюнкции и отрицания.
- •1.5 Свойства сложения по модулю два, импликации и функции Шеффера и Вебба.
- •Алгоритм приведения формулы к днф.
- •Совершенные дизъюнктивные и конъюнктивные нормальные формы.
- •Алгоритм построения скнф.
- •Алгоритм нахождения сднф путем тождественных преобразований
- •Совершенно полиноминальная нормальная форма (спнф).
- •Алгоритм построения спнф.
- •Глава 2. Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры логики.
- •2.1 Задачи и упражнения iго – типа *.
- •1.8 Методы определения линейности фал.
- •1. Использование таблиц истинности.
- •Замечательное свойство классов фал (классов Поста):
- •1.9 Функционально замкнутые классы. Критерий полноты *.
- •2. Использование полинома Жегалкина.
- •1.7 Основные классы функций алгебры логики
- •Алгоритм построения сднф.
- •2.2 Задачи и упражнения iiго – типа *.
- •1.6 Аналитические формы представления фал. Дизъюнктивные и конъюнктивные нормальные формы
- •1.3 Выражение одних элементарных функций через другие
- •1.2 Элементарные функции алгебры логики
- •Предисловие.
- •Список литературы.
Н.И. Калядин
Практикум
по дискретной математике
(часть III. Функции алгебры логики)
Учебно-методическое издание
Николай Иванович Калядин
Практикум
по дискретной математике
(часть III. Функции алгебры логики)
В авторской редакции
Компьютерная верстка Пономарев Е.В.
Подписано в печать Бумага офсетная.
Формат 60х84/16. Печать офсетная. Усл. печ. л. .
Уч.-изд. л. . Тираж 50экз. Заказ № .
Отпечатано в типографии издательства ИжГТУ.
Издательство Ижевского государственного технического
университета. 426069, Ижевск, Студенческая, 7
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
“Ижевский государственный технический университет”
Кафедра “Прикладная математика и информатика”
Н.И. Калядин
Практикум
по дискретной математике
(часть III. Функции алгебры логики)

Ижевск 2006
19. 20. 21.


22. 23. 24.
38
Оглавление.
Предисловие………………………………………………………………….......4
Функции алгебры логики……………………………………………....5
Основные определения……………………………………………….5
Элементарные функции алгебры логики……………………………6
Выражение одних элементарных функций через другие ………….8
Свойства конъюнкции, дизъюнкции и отрицания………………….9
Свойства сложения по модулю два, импликации и функции
Шеффера и Вебба ……………………………………….....................9
Аналитические формы представления ФАЛ………………………10
Основные классы функций алгебры логики ……………………….16
Методы определения линейности ФАЛ…………………………….17
Функционально замкнутые классы. Критерий полноты………….19
Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры
логики……………………………………………………………………...24
Задачи и упражнения Iго типа……………………………………….24
Задачи и упражнения IIго типа………………………………............27
Задачи и упражнения IIIго типа………………………………...........32
Список литературы……………………………………………………………..39
21. (![]()
![]() B) + (
B) + (![]()
![]() A) = (A
A) = (A![]() B) + (A
B) + (A![]() B);
B);
(![]()
![]() B)
B)![]() (
(![]()
![]() C)
C)![]() (
(![]()
![]() C);
C);
a + (c – b) = (a ~ c) + (b | c);
22. A + B = (A – B) + (B – A);
C
![]() (A
(A![]() B),если
C
B),если
C
![]() A, C
A, C![]() B;
B;
(a
![]() b)
b)![]() ((
((![]() | c)
| c)![]() (
(![]() | d) = a
| d) = a![]() b.
b.
23. (A –
B) + ((A + C)
![]() B) = (A – C) + ((A + B)
B) = (A – C) + ((A + B)![]() C);
C);
C
![]() (A
(A![]() B),если
A
B),если
A
![]() C;
C;
((a | b)
![]() (b
(b![]() c))
c))![]() (c ~ d) = d
(c ~ d) = d![]() (c
(c![]() b).
b).
24. (A + (A
– B))
![]() (1 – B) = 0;
(1 – B) = 0;
((A – C)
![]() (B – A))
(B – A))![]() (A
(A![]() B);
B);
a ~ (b | c)
= (a
![]() b) ~ (a +c)
b) ~ (a +c)![]() b.
b.
|
1. |
|
2. |
|
3. |
|
|
|
|
|
|
|
4. |
|
5. |
|
6. |
|
|
|
|
|
|