
§2. Высказывательная форма.
Высказывательные формы, которые мы рассматривали в §1, зависит только от высказывательных переменных. Высказывательные формы, встречаюшиеся не в специальных логико-математических исследованиях, а в самой математике, зависят обычно не от высказывательных, а от всяких иных (например, числовых) переменных.
В общем случае высказывательная форма может, конечно, зависеть от переменных любого вида.
Например,
выражение
 является (естественно считать) двухместной
высказывательной формой с высказывательной
переменной
является (естественно считать) двухместной
высказывательной формой с высказывательной
переменной и числовой переменной
и числовой переменной .
.
Введенные в §1 операции над высказываниями являются, очевидно, также операциями над высказывательными формами.
Рассмотрим
вопрос о соотношении между равносильностью
двух высказывательных форм
 и их эквиваленцией.
и их эквиваленцией.
I.
Если сначала
 и
и -
высказывания, то
-
высказывания, то
 есть
равносильные высказывания.
есть
равносильные высказывания.
II.
Если
 и
и -
высказывательные формы, то
-
высказывательные формы, то

Например I.
1)

2)

II.
Легко видеть, что высказывание
 истинно (т.е. высказывательные формы
истинно (т.е. высказывательные формы и
и равносильны) тогда и только тогда, когда
высказывательная форма
равносильны) тогда и только тогда, когда
высказывательная форма истинна при любых значениях переменных.
истинна при любых значениях переменных.

Областью
истинности одноместной высказывательной
формы
 называется
и через
называется
и через (или
(или )
обозначается множество тех значений
переменной
)
обозначается множество тех значений
переменной ,
при которых форма
,
при которых форма истинна.
истинна.
Т.о.,
если
 -
область значений переменной
-
область значений переменной ,
то
,
то

Иногда (1) записывают длиннее:

Пусть
 -
- - местная (
- местная ( )
высказывательная форма.
)
высказывательная форма.
Пусть
областью определения переменной
 ,
будет множество
,
будет множество
 ,
,

Областью
истинности высказывательной формы
 называется
и через
называется
и через (или
(или )
обозначается множество тех картежей
)
обозначается множество тех картежей ,
для которых
,
для которых -
истинно
-
истинно

Например:

 - действительные числа
- действительные числа


Заметим, что для данного примера

Заметим
далее, что предложения « »
и «
»
и « истинно» осмысленны, а предложения «
истинно» осмысленны, а предложения « »
и «
»
и « »
истинно бессмысленны не корректны.
»
истинно бессмысленны не корректны.
С
другой стороны (при соответствующем
смысле букв
 )
)

Понятие области истинности позволяет связать операции над множествами с операциями высказывательными формами.
а)

б)
 и если
и если ,
то
,
то
с)

Заметим
в заключение, что выражение
 может зависеть не только от
может зависеть не только от и
и ,
но и от
,
но и от и
и .
Буквы
.
Буквы и
и тоже
могут быть переменными.
тоже
могут быть переменными.
Задачи.
Выразить область истинности высказывательной формы
 через области истинности высказывательных
форм
через области истинности высказывательных
форм и
и ,
если
,
если
а)

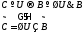
б)


§3. Кванторы.
Рассмотрим две операции, применимые только к высказывательным формам, но не к высказываниям.
Эти операции, так называемые операции навешивания кванторов, будучи примененными к высказывательной форме, приводят либо снова к высказывательной форме, либо к высказыванию.
Начнем с простейшего случая.
1)
Пусть
 - одноместная высказывательная форма
- одноместная высказывательная форма
 -
(
-
( - область значений переменной
- область значений переменной )
)
Обозначим
через
 (1)
(1)
или
если область значений переменной
 ясна
из контекста,
ясна
из контекста,
через
 (2)
(2)
следующее
высказывание: «для любого значения
переменной
 высказывание, получающееся подстановкой
этого значения в форму
высказывание, получающееся подстановкой
этого значения в форму вместо
вместо ,
истинно».
,
истинно».
Разумеется,
высказывание (1) или (2) может быть для
одной формы
 истинности, для другой – ложности.
истинности, для другой – ложности.
Иногда (1) или (2) читают короче:
«для любого

 истинно»
истинно»«для любого

 »
»
Букву
 называют квантором общности.
называют квантором общности.
(выражение
 )
и
)
и - квантором общности по переменной
- квантором общности по переменной ;
;
переход
от формы
 к высказыванию (1), (2) – навешиваем на
форму
к высказыванию (1), (2) – навешиваем на
форму квантора общности по переменной
квантора общности по переменной .
.
Обозначим через
 (3)
(3)
или
через
 (4)
(4)
следующее
высказывание: «существует такое значение
переменной
 ,
что высказывание, получающееся
подстановкой этого значения в форму
,
что высказывание, получающееся
подстановкой этого значения в форму вместо
вместо ,
истинно».
,
истинно».
Это высказывание также часто читают короче:
1)
«существует такое
 ,
что
,
что истинно»
истинно»
или
2) «существует такое
 ,
что
,
что ».
».
Буква
 называется квантором существования;
называется квантором существования;
Выражение
 и
и -квантором
существования по переменной
-квантором
существования по переменной
 ;
;
Переход
от формы
 к высказыванию (3), (4) – навешиванием на
форму
к высказыванию (3), (4) – навешиванием на
форму квантора существования по переменной
квантора существования по переменной .
.
В
выражениях (1) (4)
буква
(4)
буква является связанной переменной: навешивание
квантора связывает переменную. От
является связанной переменной: навешивание
квантора связывает переменную. От эти выражения не зависят. В то же время
эти выражения могут зависеть от
эти выражения не зависят. В то же время
эти выражения могут зависеть от и
и .
.
Если
 и
и не фиксированы, то (1)
не фиксированы, то (1) (4)
являются не высказываниями, а
высказывательными формами;
(4)
являются не высказываниями, а
высказывательными формами;
Если
же
 и
и - фиксированы, обозначают какие-то
конкретную высказывательную форму и
множество, то (1)
- фиксированы, обозначают какие-то
конкретную высказывательную форму и
множество, то (1) (4)
– высказывания.
(4)
– высказывания.
Пример:
1)
 - истинное высказывание
- истинное высказывание
2)
 - ложное высказывание
- ложное высказывание
 - истинно
- истинно
Оговорим
специально случай, когда
 .
.
 ,
(5)
,
(5)
 (6)
(6)
Квантор общности является обобщением, аналогом конъюнкции, а квантор существования – аналогом дизъюнкции на произвольное, не обязательно конечное, множество.
Пусть
 .
Тогда для любой формы
.
Тогда для любой формы :
:
 (7)
(7)
 (8)
(8)
Указанная
аналогия подкрепляется следующими
важными утверждениями, в которых область
значений переменной
 уже не обязательно конечна:
уже не обязательно конечна:
 (9)
(9)
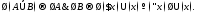 (10)
(10)
