Глава IV. Алгебра логики.

§1. Высказывание.

В главе I был введен и по мере сил разъяснен термин «высказывание» и определен термин «высказывательная форма».

Переменную, в область значений которой входят только высказывания, будут называть высказывательной переменной.

Высказывания и высказывательные переменные будем обозначать прописными латинскими буквами, а высказывательные формы – прописными готическими буквами.

Основные операции над высказываниями.

1) операция отрицания соответствует логическому союзу «и».

Эквиваленция высказыванийозначает то же, что высказывание «тогда и только тогда, когда».

Обобщение

Форма называется высказывательной, если при любом наборе своих значений, она обозначает высказывание.

Если - высказывание, то,есть также высказывания.

Если хотя бы одна из букв является высказывательной переменной, тоявляются высказывательными формами.

Дано:

Универсальным методом установления равносильности высказывательных форм, а также указания значений этих форм при каждом конкретном значении переменных является метод истинностных таблиц.

0.	Л	Л	Л	И	Л	И	Л	Л	И
1.	Л	Л	И	И	Л	И	Л	Л	И
2.	Л	И	Л	И	И	И	Л	И	Л
3.	Л	И	И	И	И	И	Л	И	Л
4.	И	Л	Л	Л	Л	Л	И	И	Л
5.	И	Л	И	Л	Л	И	Л	Л	И
6.	И	И	Л	Л	Л	Л	И	И	Л
7.	И	И	И	Л	Л	И	Л	Л	И

Высказывательные формы иназывается равносильными если на всех наборах своих знчений высказывательных переменных они принимают одинаковые значения.

Условимся о силе связи знаков

1)

2)

3)

4)5)6)

Например: .,

что означает:

Примеры простейших равносильностей высказывательных форм с высказывательными переменными:

I группа:

(I) 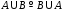коммутация,

(II) ассоциация,

(III) дистрибутивность,

(IV) поглощения,

(V) идемпотентность.

Двойственные равносильности.

(I)’ коммутация.

(II)’ ассоциация.

(III)’ дистрибутивность.

(IV)’ поглощения.

(V)’ идемпотентность.

II группа:

(I) ..

(II) ..

(III) ..

(IV) ..

III группа:

(I) - закон двойного отрицания

(II)

(III)

(IV)

IV группа:

(I)

(II) (закон контрапозиции)

(III)

(IV) (закон исключенного третьего)

Перечисленные равносильности выражают наиболее важные (для практического применения в математике) свойства операций .

Знание этих равносильностей позволяет более изящно (нежели метод таблиц истинности) устанавливать истинность других равносильностей.

Например:

Рассмотрим приложение высказываний к доказательству теорем (начала исчисления высказываний):

Рассмотрим теорему (1)

Чтобы доказать эту теорему, достаточно доказать, например, что посылка ложна (в силу таблицы истинности для импликации эта теорема будет истинна тривиальным образом).

Достаточно доказать также, что заключение истинно.

В этом случае, в силу определения импликации, теорема (1) также будет истинной.

Однако случаи, когда верность теоремы (1) удается доказать одним из двух указанных путей, сравнительно редки.

Поэтому наиболее часто встречающимся на практике, наиболее естественным путем доказательства теоремы (1) является следущий:

Предположим, что посылка истинна, и попробуем вывести из этого предположения, что заключениетоже истинно.

Если теорема (1) имеет вид: (условие является конъюнкцией):

, (2)

то, чтобы доказать ее нужно из предположения об истинности (одновременно) посылок ивывести истинность заключения.

Если условие теоремы (1) является дизъюнкцией, т.е. теорема (1) имеет вид:

(3)

то предположение об истинности посылки распадается на два случая:

1) истинно

2) истинно

Нужно рассмотреть два этих случая и в каждом из них доказать, что истинно.

Пусть теперь заключение теоремы (1) является конъюнкцией, т.е. теорема имеет вид

(4)

В этом случае из предположения об истинности нужно вывести истинность заключения, т.е. истинностьи истинность.

Пусть заключение теоремы (1) является дизъюнкцией, т.е. теорема имеет вид:

(5)

Наиболее удобный путь доказательства такой теоремы – замена дизъюнкции равносильностью, т.е.

Т.о. доказываются «многочленные» дизъюнкции:

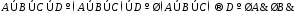
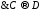
Т.е. для доказательства теоремы вида нужно из предположения о ложностиивывести истинность.

Очень часто заключение теоремы (1) является импликацией, т.е. сама теорема имеет вид «двухступенчатой» импликации:

Тогда используя равносильность доказывают:

Полезно уяснить разницу между доказательством теоремы (1) по закону контрапозиции и доказательством «от противного».

Напомним:

1. схема доказательства по закону контрапозиции:

2. схемы доказательства от противного:

а)

б)

в)

Приложения исчисления высказываний к задачам формальных доказательств.

Пример 1. .

2. Если завтра выпадет снег, то можно буднт кататься на лыжах:

3. Если числа иудовлетворяют условиям:

,,, то выполняется неравенство

Пусть

4. Некто держит в руке (неизвестно в правой или левой) монету. Известно, чтовсегда лжет или всегда говорит правду (но неизвестно что именно). Как с помощью единственного вопроса узнать, в какой руке находится монета?

Решение: Ввести два высказывания:

- монета в правой руке (- в левой)

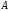-говорит правду (- неправду)

Вопрос: «Верно ли, что либо у тебя монета в правой руке, либо ты правдив?»

отвечает: да – в правой руке; нет – в левой руке.

,.

.