
§6. График.
График – является одним из важнейших понятий.
График
- это множество пар, т.е. множество,
каждый элемент которого является парой,
или, по-другому, множество
 называется
графиком, если каждый его элемент есть
пара.
называется
графиком, если каждый его элемент есть
пара.
Например,
1) множество
 (пустой график)
(пустой график)
2)

Если
 -
произвольное множество, то
-
произвольное множество, то и любое
и любое являются
графиками.
являются
графиками.

Рис 1-6.
На
рисунках 1-6 изображены графики, являющиеся
подмножеством множества

Из этих рисунков видно, что наше понятие графика является обобщением известного из школы понятия графика функции.
Если
 и
и - произвольные множества, то
- произвольные множества, то и любое
и любое являются графиками
являются графиками
Областью
определения графика
 называется множество
называется множество
Областью
значений графика
 называется множество
называется множество

P
Легко
видеть, что если
 -
график, то
-
график, то
 или
или
 (1)
(1)
или
 и
и (2)
(2)
Операции над графиками.
Введем две операции над графиками.
Одна из этих операций (инверсия графика) будет одноместной; другая (композиция графиков – двуместная).
Инверсия графика определяется через инверсию пары.
Пара
 называется инверсией пары
называется инверсией пары ,
если
,
если ,
,
Т.о.,
если
 ,
то
,
то -
инверсия пары
-
инверсия пары
Очевидно,
 (3)
(3)
Инверсией
графика
 называется множество инверсий пар из
называется множество инверсий пар из

 -
инверсия графика
-
инверсия графика
 (4)
(4)
 (5)
(5)
из
(3) вытекает, что

Легко видеть, что
 ,
(7)
,
(7)
 (8)
(8)
т.е.
область определения инверсии графика
 равна области значений графика
равна области значений графика и область значений инверсии графика
и область значений инверсии графика равна области определения графика
равна области определения графика .
.










График
 называется симметричным, если он наряду
с любой своей парой содержит её инверсию,
т.е. если
называется симметричным, если он наряду
с любой своей парой содержит её инверсию,
т.е. если
 .
.
Примеры:
1)


2)

3)

Легко
видеть, что каково бы ни было множество
 ,
, является симметричным графиком. Если
является симметричным графиком. Если -
произвольный график, то
-
произвольный график, то являются симметричными графиками.
являются симметричными графиками.


Выведем одно простое обозначение, которое нам часто будет полезно в дальнейшем.
Пусть
 -
произвольное множество.
-
произвольное множество.
Обозначим
через
 множество
пар вида
множество
пар вида ,
где
,
где пробегает
все множество
пробегает
все множество .
.
Т.о.,
 .
.
Если
 ,
то
,
то .
.
 ,
то
,
то
Очевидно,
 .
.
Множество
 является симметричным графиком.
является симметричным графиком.
 иногда называют диагональю множества
иногда называют диагональю множества .
.
Слово «симметричный» в термине «симметричный график» вызвано следующим.
Легко
доказать, что если
 ,
то точки на координатной плоскости,
изображающие пары
,
то точки на координатной плоскости,
изображающие пары и
и ,
симметричны относительно прямой
,
симметричны относительно прямой .
Отсюда вытекает, что график
.
Отсюда вытекает, что график тогда и только тогда является симметричным
графиком, когда соответствующее множество
точек на координатной плоскости
симметрично относительно прямой
тогда и только тогда является симметричным
графиком, когда соответствующее множество
точек на координатной плоскости
симметрично относительно прямой .
Отсюда вытекает также, что инверсия
.
Отсюда вытекает также, что инверсия графика
графика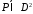 получается зеркальным отражением
графика
получается зеркальным отражением
графика в прямой
в прямой .
.
Многие
свойства произвольных симметричных
графиков легко усматриваются ка
координатной плоскости.
Легко
видеть, что для графика

 -
симметричный
-
симметричный
 (9)
(9)
 -
симметричный
-
симметричный
 -
симметричный. (10)
-
симметричный. (10)
Операция композиции.
График
 называется композицией графиков
называется композицией графиков и
и ,
если
,
если тогда и только тогда, когда существует
такое
тогда и только тогда, когда существует
такое ,
что
,
что и
и .
.
Переход
от графиков
 к их композиции
к их композиции будем называть компонированием графиков
будем называть компонированием графиков и
и .
.
Если, например

то

Очевидно,
 (11)
(11)



Следовательно,
для любого графика
 (12)
(12)

Если
 -произвольное
множество
и
-произвольное
множество
и
 ,
то
,
то (13)
(13)
Если
композицию графиков сопоставить с
умножением чисел, то роль нуля в этом
«умножении» будет, в силу (12), играть
пустой график
 ,
роль, аналогичную роли единицы, в силу
(13), - диагональ
,
роль, аналогичную роли единицы, в силу
(13), - диагональ .
.
Сходство усиливается свойством (14) – «умножение» графиков ассоциативно.
Легко
доказать, что для любых 3-х графиков
 (14)
(14)
(14)
верно и для любого (конечного) числа
графиков, т.е. можно записать для любой
расстановки скобок:

Операции композиции и инверсии связаны следующим равенством:
 (15)
(15)
 (16)
(16)
*Композиция
 произвольного конечного числа графиков
есть результат последовательного
попарного компонирования графиков
произвольного конечного числа графиков
есть результат последовательного
попарного компонирования графиков
 при любой расстановке скобок.
при любой расстановке скобок.
Например.





Рассмотрим два свойства графиков.


График
 называется функциональным, если в нем
нет пар с одинаковыми первыми и различными
вторыми компонентами.
Функциональный график – это график, не
содержащий пар вида:
называется функциональным, если в нем
нет пар с одинаковыми первыми и различными
вторыми компонентами.
Функциональный график – это график, не
содержащий пар вида:
График
 называется инъективным, если в нем нет
пар с различными первыми и одинаковыми
вторыми компонентами.
называется инъективным, если в нем нет
пар с различными первыми и одинаковыми
вторыми компонентами.
Инъективный
график – это график, не содержащий пар
вида:
Пустой
график
 и любой одноэлементный график тривиальным
образом функциональны и инъективны.
и любой одноэлементный график тривиальным
образом функциональны и инъективны.
Если
множество
 содержит более одного элемента, то
график
содержит более одного элемента, то
график не функционален и не инъективен.
не функционален и не инъективен.

График
 - инъективен, но не функционален
- инъективен, но не функционален

График
 - инъективен, но не функционален
- инъективен, но не функционален

Заметим
еще, что если график
 функционален и
функционален и ,
то график
,
то график функционален
(раз в
функционален
(раз в нет «запущенных» пар, то тем более их
нет в
нет «запущенных» пар, то тем более их
нет в ).
Аналогичное утверждение (по той же
причине) верно и для инъективности.
).
Аналогичное утверждение (по той же
причине) верно и для инъективности.
Чрезвычайно полезными будут нам в дальнейшем два следующих простых утверждения: композиция функциональных графиков есть снова функциональный график ( по-другому: композиция сохраняет функциональность), композиция инъективных графиков инъективна.
Докажем,
например, первое утверждение, а именно:
если график
 -
функционален и график
-
функционален и график функционален, то их композиция – график
функционален, то их композиция – график функционален.
функционален.

Используя для этого закон контрапозиции. Докажем вместо сформулированной теоремы равносильное ей утверждение:
если
график
 не функционален, то не верно, что график
не функционален, то не верно, что график функционален и график
функционален и график функционален.
функционален.
Итак,
пусть график
 не функционален.
не функционален.
Тогда в нем есть пары с одинаковыми первыми и различными вторыми компонентами.
Пусть
это будут пары
 .
.
Имеем
 (1)
(1)
 (2)
(2)
 (3)
(3)
Из
(1) и определения композиции следует,
что существует такое
 ,
что
,
что
 (4)
(4)
 (5)
(5)
Аналогично
из (2) получаем, что существует такое
 ,
что
,
что
 (6)
(6)
 (7)
(7)
Если
 ,
то (3),(5),(7) влекут, что график
,
то (3),(5),(7) влекут, что график не функционален (что противоречит
условию ).
не функционален (что противоречит
условию ).
Если
 ,
то (4),(6) влекут, что график
,
то (4),(6) влекут, что график не функционален (что также противоречит
исходному условию теоремы).
не функционален (что также противоречит
исходному условию теоремы).
Аналогично доказывается, что композиция инъективных графиков инъективна.
