Глава 2. Исчисление высказываний (ив).

§1. Аксиоматический метод.

В данной главе на примере изучения исчислений высказываний(ИВ) будет разобран один из основных методов построения абстрактных теорий в математике так называемый, аксиоматический метод. Согласно главной идее этого метода построения какой-либо абстрактной математической теории осуществляется с помощью задания определенной формальной системы.

Формальная система включает четыре понятия:

1. Язык

2. Аксиомы

3. Правила вывода

4. Доказательство

1. Язык формальной системы – это набор символов и правил комбинирования этими символами для образования формул. Язык состоит из алфавита (множества исходных символов) и словаря. Словарем является множество правильно образованных формул.

Формулой, или словом, называется любая конечная последовательность исходных символов. Однако, как и в обычном языке, целесообразно рассматривать только осмысленные слова или формулы. С этой целью некоторые формулы языка объявляются простейшими, правильно образованными формулами(ПОФ) и указывается правило образования сложных ПОФ из простейших.

2. Аксиомы.

Некоторые ПОФ объявляются аксиомами, т.е. тождественно истинными утверждениями, не требующими доказательств (априорно, т.е. по определению, бездоказательно).

3. Правила вывода.

Это правила, позволяющие от одной группы формул перейти к другой. О полученной таким образом формуле говорят, что она выведена из исходной группы формул.

4. Доказательство.

Это есть конечная последовательность ПОФ, каждая из которых является либо аксиомой, либо является результатом применения одного из правил вывода к предыдущим формулам этой последовательности. Последняя формула в доказательстве называется доказуемой или теоремой.

Заметим, что в данной главе применяется аксиоматический метод к ИВ. Как и ранее, нас интересует высказывание на предмет истинности или ложности и не интересует их содержание. Мы подчеркнем связь алгебры высказываний из главы 1 и исчислением высказываний из главы 2.

Алгебра высказываний опиралась на содержательный подход к изучению высказываний, а ИВ опирается на формальный подход к изучению высказываний. Наша задача убедится в равносильности этих двух подходов.

Аксиоматический метод более удобен в сложных математических рассуждениях.

§2. Исчисление высказываний.

Определение 1. Язык ИВ

1. Язык включает алфавит, основными символами алфавита являются:

а) высказываемые переменные (A, B, C, D,…,A₁,B₁,…)

б) логические символы (┐,&,v,→,≡)

в) вспомогательные символы (скобки): (,); [,]; {,}

2. ПОФ будем определять строго методом математической индукции. В соответствии с математической индукцией мы определяем:

а) высказываетельные переменные – ПОФ (объявление переменных ПОФ)

б) пусть каким-либо образом определено некоторое множество ПОФ

в) если A, B – ПОФ, то в соответствии с логическими символами, введенными в п.2, мы можем образовать более сложные ПОФ.

- ПОФ

г) других ПОФ нет.

Пример 1. A, B – ПОФ

а) (A→BC) – не ПОФ, т.к. не определен порядок выполнения операций: →,

б) ((A→B) C) – ПОФ

Скобки играют роль вспомогательных символов для однозначности чтения.

(ABC) – не ПОФ,

Определение 2. (Аксиомы) В качестве аксиом возьмем четыре группы формул:

Формулы I-IV являются фактически схемами аксиом, то есть каждая схема аксиом определяет бесконечное множество или число аксиом, так как постановкой вместо конкретных высказываний A, B, C … мы будем получать конкретные аксиомы.

Определение 3. Единственное правило, которое будем применять – это правило отделения (ПО), (или правило модус поненс - М.Р.) – это процедура перехода от 2-х формул вида к заключению В.

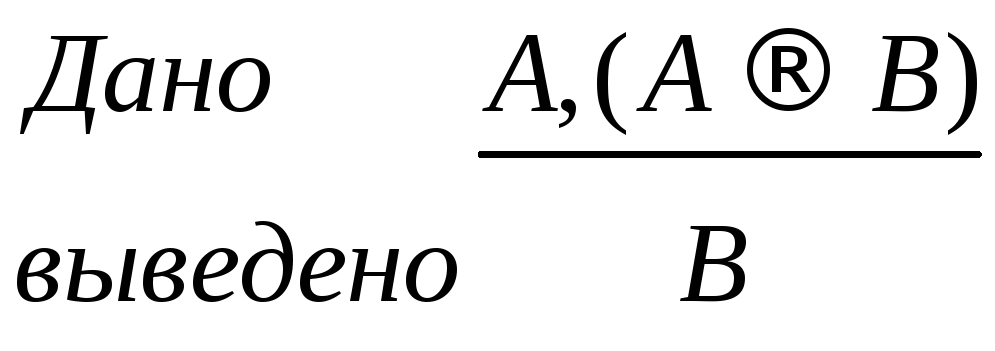
Пример 2.

Определение 4. Доказательством или выводом в исчислении

высказываний называется конечная последовательность формул, каждая из которых есть либо аксиома, либо получается по правилу МР из предыдущих формул этой последовательности. Формула А называется доказуемой, или выводимой, если существует конечный вывод {В₁,…,В_к}, в котором последняя формула В_к есть А. Факт выводимости обозначения ├А - формула А выводима или доказуема в ИВ.

Пример 3. А→А, где А – ПОФ

Определение 5. Пусть дана последовательность формул A₁,…,A_m. Будем говорить, что формула А выводима из гипотез A₁,…,A_m, если существует конечная последовательность формул B₁,…,B_k, каждая из которых есть либо аксиома, либо получена по правилу МР из гипотез A₁,…,A_m с учетом предыдущих формул этой последовательности. Последнее выражение B_k=A. Тогда факт выводимости формулы А из {B₁,…,B_k} обозн.: A₁,…,A_m├А

Пример 4. ├ С

Доказательство:

Нами дано строгое определение понятия математического доказательства. В дальнейшем наша цель изучить конкретные виды таких доказательств.