ТРПО / Материалы по ТП / Пошаг_детализ_1

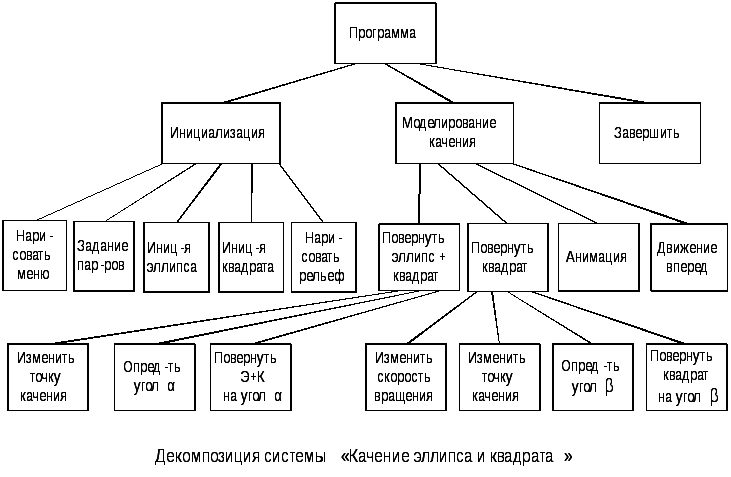
Основная программа

Инициализация

Моделирование качения

Завершить

Инициализация

Нарисовать меню

Задание параметров

Инициализация эллипса

Инициализация квадрата

Нарисовать рельеф качения

Моделирование качения

Цикл До прохождения экрана

Повернуть эллипс+квадрат

Повернуть квадрат

Анимация

Движение вперед

Все-Цикл

Инициализация эллипса

Задать массив точек эллипса E

Задать массив точек контакта квадрата и эллипса V

Задать т. качения еОs(x,y)

Задать центр эллипса e0(x,y)

Инициализация эллипса

Вычислить координаты точек эллипса по формулам:

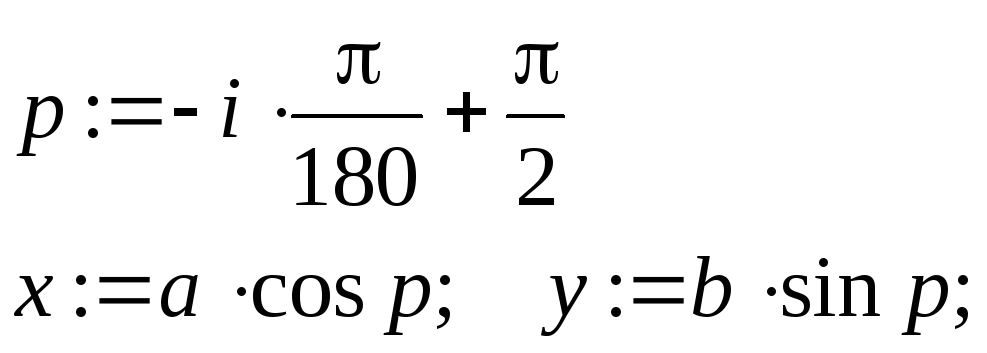i – угол в градусах

Выбрать каждую l-точку (l=10) и сформ-ть массив E;

Cформ-ть массив т. контакта квадрата и эллипса V по условию:

Dist(V[i],V[i+1])=ak;

Задать т. качения еОs

Задать центр эллипса e0.

Все-Инициализация эллипса

Инициализация квадрата

Задать массив точек квадрата K

Задать т. качения kОs(x,y)

Поворот точки вокруг заданной оси

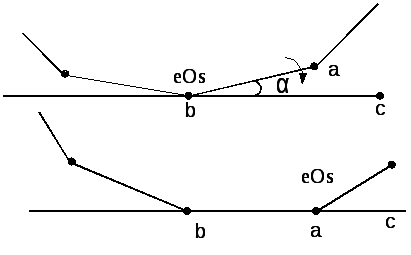
Повернуть эллипс+квадрат ( i ) ; i - номер актуальной вершины эллипса

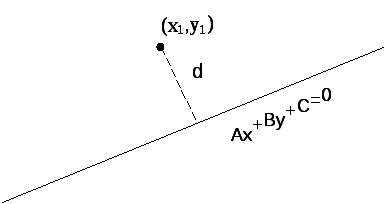
Проверить на смещение точки качения еОs(x_i,y_i)

Определить угол α

Повернуть точки E, К, V, kОs относительно т. еОs(x_i,y_i) на угол α

Повернуть эллипс+квадрат( i ); i – номер актуальной т. эллипса

Если fe=0 То еОs:=E[i] fe – признак «α=0»

α:=Ugol(E[i+1].x, E[i+1].y, еОs.x, eOs.y, MaxX, b);

Если α>grad То α:= grad ; fe:=1;

Иначе fe:=0;

Rotate(α, E,eOs);

Rotate(α,K,eOs);

Rotate(α,V,eOs);

Rotate(α,kOs,eOs);

Все-Повернуть эллипс+квадрат

Повернуть квадрат ( j ) ; j - номер актуальной вершины квадрата

Проверить на изменение скорости вращения квадрата

Проверить на изменение точки качения kОs(x_j,y_j)

Определить угол β

Повернуть точки К относительно т. kОs(x_j,y_j) на угол β

Повернуть квадрат ( j , t); j - номер актуальной вершины квадрата;

t - номер актуальной точки контакта квадрата

и эллипса

Если x_цэ > x_цk

То ∆β:=2*grad Иначе ∆β := grad; ∆β – шаг поворота квадрата

Если fk = 0 fk – признак «β =0»

То kOs:=V[t]; j:=Succ(j);

β:=Ugol(K[j+1].x, K[j+1].y, kOs.x, kOs.y, V[t+1].x, V[t+1].y) ;

Если β >∆β То β := ∆β; fk:=1;

Иначе fk:=0;

Rotate(β, K, kOs);

Все-Повернуть квадрат;

Программа

Нарисовать меню

Задание параметров

Инициализация эллипса

Инициализация квадрата

Нарисовать рельеф качения

Цикл До прохождения экрана

Изменить т. качения эллипса

Определить угол α

Повернуть E и К на угол α

Изменить скорость вращ. квадрата

Изменить т. качения квадрата

Определить угол β

Повернуть квадрат на угол β

Анимация

Модифицировать параметры

Все-Цикл

Все-Программа

Программа

Нарисовать меню

Задание параметров

Вычислить координаты точек эллипса по формулам:

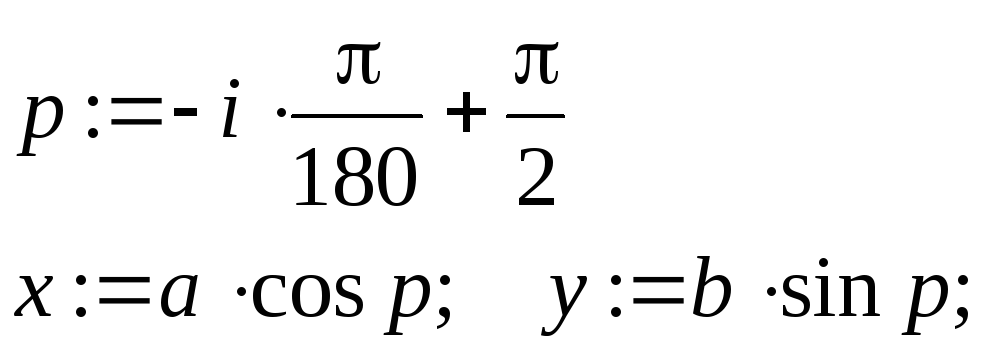i – угол в градусах

Выбрать каждую l-точку (l=10) и сформ-ть массив E;

Cформ-ть массив т. контакта квадрата и эллипса V по условию:

Dist(V[i],V[i+1])=ak;

Задать т. качения еОs

Задать центр эллипса e0.

Задать массив точек квадрата K

Задать т. качения kОs(x,y)

Нарисовать рельеф качения

Цикл До прохождения экрана

Если fe=0 То еОs:=E[i] fe – признак «α=0»

α:=Ugol(E[i+1].x, E[i+1].y, еОs.x, eOs.y, MaxX, b);

Если α>grad То α:= grad ; fe:=1;

Иначе fe:=0;

Rotate(α, E,eOs);

Rotate(α,K,eOs);

Rotate(α,V,eOs);

Rotate(α,kOs,eOs);

Если x_цэ > x_цk

То ∆β:=2*grad Иначе ∆β := grad; ∆β – шаг поворота квадрата

Если fk = 0 fk – признак «β =0»

То kOs:=V[t]; j:=Succ(j);

β:=Ugol(K[j+1].x, K[j+1].y, kOs.x, kOs.y, V[t+1].x, V[t+1].y) ;

Если β >∆β То β := ∆β; fk:=1;

Иначе fk:=0;

Rotate(β, K, kOs);

Анимация

Модифицировать параметры

Все-Цикл

Все-Программа

модель предметной области

Полезные формулы: