

CHAPTER 4 The Value of Common Stocks |
87 |
that next year Icarus plans to double in size by issuing an additional one million shares at $100 a share. Everything will be the same as before but twice as big. Thus from year 2 onward the company earns a constant $20 million, all of which is paid out as dividends on the 20 million shares. What is the value of the company? What is the value of each existing Icarus Air share?
23.Look one more time at Table 4.1, which applies the DCF stock valuation formula to Fledgling Electronics. The CEO, having just learned that stock value is the present value of future dividends, proposes that Fledgling pay a bumper dividend of $15 a share in period 1. The extra cash would have to be raised by an issue of new shares. Recalculate Table 4.1 assuming that profits and payout ratios in all subsequent years are unchanged. You should find that the total present value of dividends per existing share is unchanged at $100. Why?
1.Look again at Tables 4.3 (Growth-Tech) and 4.7 (Concatenator Manufacturing). Note the discontinuous increases in dividends and free cash flow when asset growth slows down. Now look at your answer to Practice Question 11: Dividends are expected to grow smoothly, although at a lower rate after year 3. Is there an error or hidden inconsistency in Practice Question 11? Write down a general rule or procedure for deciding how to forecast dividends or free cash flow.
2.The constant-growth DCF formula
DIV1
P0 r g
is sometimes written as
P0 |
ROE11 b 2BVPS |
|
|
bROE |
|
|
r |
|
CHALLENGE QUESTIONS
where BVPS is book equity value per share, b is the plowback ratio, and ROE is the ratio of earnings per share to BVPS. Use this equation to show how the price-to-book ratio varies as ROE changes. What is price-to-book when ROE r?
3.Portfolio managers are frequently paid a proportion of the funds under management. Suppose you manage a $100 million equity portfolio offering a dividend yield
(DIV1/P0) of 5 percent. Dividends and portfolio value are expected to grow at a constant rate. Your annual fee for managing this portfolio is .5 percent of portfolio value and is calculated at the end of each year. Assuming that you will continue to manage the portfolio from now to eternity, what is the present value of the management contract?
MINI-CASE
Reeby Sports
Ten years ago, in 1993, George Reeby founded a small mail-order company selling highquality sports equipment. Reeby Sports has grown steadily and been consistently profitable (see Table 4.8). The company has no debt and the equity is valued in the company’s books at nearly $41 million (Table 4.9). It is still wholly owned by George Reeby.
George is now proposing to take the company public by the sale of 90,000 of his existing shares. The issue would not raise any additional cash for the company, but it would allow
88 |
PART I Value |
T A B L E 4 . 8
Summary income data (figures in $ millions).
Note: Reeby Sports has never paid a dividend and all the earnings have been retained in the business.
|
1999 |
2000 |
2001 |
2002 |
2003 |
|
|
|
|
|
|
Cash flow |
5.84 |
6.40 |
7.41 |
8.74 |
9.39 |
Depreciation |
1.45 |
1.60 |
1.75 |
1.97 |
2.22 |
Pretax profits |
4.38 |
4.80 |
5.66 |
6.77 |
7.17 |
Tax |
1.53 |
1.68 |
1.98 |
2.37 |
2.51 |
Aftertax profits |
2.85 |
3.12 |
3.68 |
4.40 |
4.66 |
|
|
|
|
|
|
T A B L E 4 . 9
Summary balance sheet for year ending December 31st (figures in $ millions).
Note: Reeby Sports has 200,000 common shares outstanding, wholly owned by George Reeby.
Assets |
|
|
|
|
Liabilities and Equity |
|
|
|
|
|
|
|
|
|
|
|
2002 |
2003 |
|
|
2002 |
2003 |
|
|
|
|
|
|
|
||
Cash & securities |
3.12 |
3.61 |
Current liabilities |
2.90 |
3.20 |
||
Other current assets |
15.08 |
16.93 |
|
|
|
|
|
Net fixed assets |
20.75 |
23.38 |
Equity |
36.05 |
40.71 |
||
Total |
38.95 |
43.91 |
Total |
38.95 |
43.91 |
||
|
|
|
|
|
|
|
|
George to cash in on part of his investment. It would also make it easier to raise the substantial capital sums that the firm would later need to finance expansion.
George’s business has been mainly on the East Coast of the United States, but he plans to expand into the Midwest in 2005. This will require a substantial investment in new warehouse space and inventory. George is aware that it will take time to build up a new customer base, and in the meantime there is likely to be a temporary dip in profits. However, if the venture is successful, the company should be back to its current 12 percent return on book equity by 2010.
George settled down to estimate what his shares are worth. First he estimated the profits and investment through 2010 (Tables 4.10 and 4.11). The company’s net working capital includes a growing proportion of cash and marketable securities which would help to meet the cost of the expansion into the Midwest. Nevertheless, it seemed likely that the company would need to raise about $4.3 million in 2005 by the sale of new shares. (George distrusted banks and was not prepared to borrow to finance the expansion.)
Until the new venture reached full profitability, dividend payments would have to be restricted to conserve cash, but from 2010 onward George expected the company to pay out about 40 percent of its net profits. As a first stab at valuing the company, George assumed that after 2010 it would earn 12 percent on book equity indefinitely and that the cost of capital for the firm was about 10 percent. But he also computed a more conservative valuation, which recognized that the mail-order sports business was likely to get intensely competitive by 2010. He also looked at the market valuation of a comparable business on the West Coast, Molly Sports. Molly’s shares were currently priced at 50 percent above book value and were selling at a prospective price–earnings ratio of 12 and a dividend yield of 3 percent.
George realized that a second issue of shares in 2005 would dilute his holdings. He set about calculating the price at which these shares could be issued and the number of shares that would need to be sold. That allowed him to work out the dividends per share and to check his earlier valuation by calculating the present value of the stream of pershare dividends.

|
|
|
|
CHAPTER 4 |
The Value of Common Stocks |
89 |
||
|
|
|
|
|
|
|
|
|
|
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
|
|
|
|
|
|
|
|
|
Cash flow |
10.47 |
11.87 |
7.74 |
8.40 |
9.95 |
12.67 |
15.38 |
|
Depreciation |
2.40 |
3.10 |
3.12 |
3.17 |
3.26 |
3.44 |
3.68 |
|
Pretax profits |
8.08 |
8.77 |
4.62 |
5.23 |
6.69 |
9.23 |
11.69 |
|
Tax |
2.83 |
3.07 |
1.62 |
1.83 |
2.34 |
3.23 |
4.09 |
|
Aftertax profits |
5.25 |
5.70 |
3.00 |
3.40 |
4.35 |
6.00 |
7.60 |
|
Dividends |
2.00 |
2.00 |
2.50 |
2.50 |
2.50 |
2.50 |
3.00 |
|
Retained profits |
3.25 |
3.70 |
.50 |
.90 |
1.85 |
3.50 |
4.60 |
|
|
|
|
|
|
|
|
|
|
T A B L E 4 . 1 0
Forecasted profits and dividends (figures in $ millions).
|
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
|
|
|
|
|
|
|
|
Gross investment |
|
|
|
|
|
|
|
in fixed assets |
4.26 |
10.50 |
3.34 |
3.65 |
4.18 |
5.37 |
6.28 |
Investments in net |
|
|
|
|
|
|
|
working capital |
1.39 |
.60 |
.28 |
.42 |
.93 |
1.57 |
2.00 |
Total |
5.65 |
11.10 |
3.62 |
4.07 |
5.11 |
6.94 |
8.28 |
|
|
|
|
|
|
|
|
T A B L E 4 . 1 1
Forecasted investment expenditures (figures in $ millions).
Questions
1.Use Tables 4.10 and 4.11 to forecast free cash flow for Reeby Sports from 2004 to 2010. What is the present value of these cash flows in 2003, including PV(horizon value) in 2010?
2.Use the information given for Molly Sports to check your forecast of horizon value. What would you recommend as a reasonable range for the present value of Reeby Sports?
3.What is the present value of a share of stock in the company? Give a reasonable range.
4.Reeby Sports will have to raise $4.3 million in 2005. Does this prospective share issue affect the per-share value of Reeby Sports in 2003? Explain.

C H A P T E R F I V E
WHY NET PRESENT
VALUE LEADS TO
BETTER INVESTMENT
DECISIONS THAN
OTHER CRITERIA

IN THE FIRST four chapters we introduced, at times surreptitiously, most of the basic principles of the investment decision. In this chapter we begin by consolidating that knowledge. We then take a look at three other measures that companies sometimes use when making investment decisions. These are the project’s payback period, its book rate of return, and its internal rate of return. The first two of these measures have little to do with whether the project will increase shareholders’ wealth. The project’s internal rate of return—if used correctly—should always identify projects that increase shareholder wealth. However, we shall see that the internal rate of return sets several traps for the unwary.
We conclude the chapter by showing how to cope with situations when the firm has only limited capital. This raises two problems. One is computational. In simple cases we just choose those projects that give the highest NPV per dollar of investment. But capital constraints and project interactions often create problems of such complexity that linear programming is needed to sort through the possible alternatives. The other problem is to decide whether capital rationing really exists and whether it invalidates net present value as a criterion for capital budgeting. Guess what? NPV, properly interpreted, wins out in the end.
5.1 A REVIEW OF THE BASICS
Vegetron’s chief financial officer (CFO) is wondering how to analyze a proposed $1 million investment in a new venture called project X. He asks what you think.
Your response should be as follows: “First, forecast the cash flows generated by project X over its economic life. Second, determine the appropriate opportunity cost of capital. This should reflect both the time value of money and the risk involved in project X. Third, use this opportunity cost of capital to discount the future cash flows of project X. The sum of the discounted cash flows is called present value (PV). Fourth, calculate net present value (NPV) by subtracting the $1 million investment from PV. Invest in project X if its NPV is greater than zero.”
However, Vegetron’s CFO is unmoved by your sagacity. He asks why NPV is so important.
Your reply: “Let us look at what is best for Vegetron stockholders. They want you to make their Vegetron shares as valuable as possible.”
“Right now Vegetron’s total market value (price per share times the number of shares outstanding) is $10 million. That includes $1 million cash we can invest in project X. The value of Vegetron’s other assets and opportunities must therefore be $9 million. We have to decide whether it is better to keep the $1 million cash and reject project X or to spend the cash and accept project X. Let us call the value of the new project PV. Then the choice is as follows:
|
|
|
Market Value ($ millions) |
||||
|
|
|
|
|
|
|
|
Asset |
Reject Project X |
Accept Project X |
|||||
|
|
|
|
|
|
|
|
Cash |
1 |
|
0 |
|
|||
Other assets |
9 |
|
9 |
|
|||
Project X |
|
0 |
|
|
PV |
|
|
|
10 |
|
9 PV |
||||
|
|
|
|
|
|
|
|
91
92 |
PART I Value |
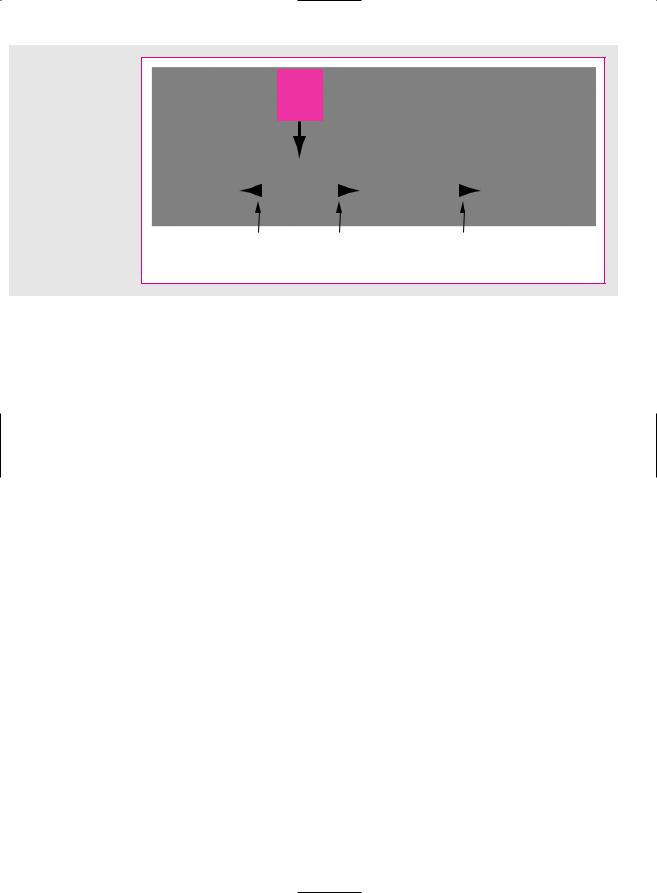
F I G U R E 5 . 1
The firm can either keep and reinvest cash or return it to investors. (Arrows represent possible cash flows or transfers.) If cash is reinvested, the opportunity cost is the expected rate of return that shareholders could have obtained by investing in financial assets.
Cash
Investment |
|
|
Firm |
|
|
Shareholders |
|
|
Investment |
|
opportunity |
|
|
|
|
|
|
opportunities |
|||
|
|
|
|
|
|
|||||
(real asset) |
|
|
|
|
|
|
|
|
|
(financial assets) |
|
|
|
|
|
|
|
|
|
|
|
|
Invest |
Alternative: |
Shareholders |
|||||||
|
|
|
pay dividend |
invest for themselves |
||||||
|
|
|
to shareholders |
|
|
|
|
|||
“Clearly project X is worthwhile if its present value, PV, is greater than $1 million, that is, if net present value is positive.”
CFO: “How do I know that the PV of project X will actually show up in Vegetron’s market value?”
Your reply: “Suppose we set up a new, independent firm X, whose only asset is project X. What would be the market value of firm X?
“Investors would forecast the dividends firm X would pay and discount those dividends by the expected rate of return of securities having risks comparable to firm X. We know that stock prices are equal to the present value of forecasted dividends.
“Since project X is firm X’s only asset, the dividend payments we would expect firm X to pay are exactly the cash flows we have forecasted for project X. Moreover, the rate investors would use to discount firm X’s dividends is exactly the rate we should use to discount project X’s cash flows.
“I agree that firm X is entirely hypothetical. But if project X is accepted, investors holding Vegetron stock will really hold a portfolio of project X and the firm’s other assets. We know the other assets are worth $9 million considered as a separate venture. Since asset values add up, we can easily figure out the portfolio value once we calculate the value of project X as a separate venture.
“By calculating the present value of project X, we are replicating the process by which the common stock of firm X would be valued in capital markets.”
CFO: “The one thing I don’t understand is where the discount rate comes from.” Your reply: “I agree that the discount rate is difficult to measure precisely. But it is easy to see what we are trying to measure. The discount rate is the opportunity
cost of investing in the project rather than in the capital market. In other words, instead of accepting a project, the firm can always give the cash to the shareholders and let them invest it in financial assets.
“You can see the trade-off (Figure 5.1). The opportunity cost of taking the project is the return shareholders could have earned had they invested the funds on their own. When we discount the project’s cash flows by the expected rate of return on comparable financial assets, we are measuring how much investors would be prepared to pay for your project.”

CHAPTER 5 Why Net Present Value Leads to Better Investment Decisions Than Other Criteria |
93 |
“But which financial assets?” Vegetron’s CFO queries. “The fact that investors expect only 12 percent on IBM stock does not mean that we should purchase Fly- by-Night Electronics if it offers 13 percent.”
Your reply: “The opportunity-cost concept makes sense only if assets of equivalent risk are compared. In general, you should identify financial assets with risks equivalent to the project under consideration, estimate the expected rate of return on these assets, and use this rate as the opportunity cost.”
Net Present Value’s Competitors
Let us hope that the CFO is by now convinced of the correctness of the net present value rule. But it is possible that the CFO has also heard of some alternative investment criteria and would like to know why you do not recommend any of them. Just so that you are prepared, we will now look at three of the alternatives. They are:
1.The book rate of return.
2.The payback period.
3.The internal rate of return.
Later in the chapter we shall come across one further investment criterion, the profitability index. There are circumstances in which this measure has some special advantages.
Three Points to Remember about NPV
As we look at these alternative criteria, it is worth keeping in mind the following key features of the net present value rule. First, the NPV rule recognizes that a dollar today is worth more than a dollar tomorrow, because the dollar today can be invested to start earning interest immediately. Any investment rule which does not recognize the time value of money cannot be sensible. Second, net present value depends solely on the forecasted cash flows from the project and the opportunity cost of capital. Any investment rule which is affected by the manager’s tastes, the company’s choice of accounting method, the profitability of the company’s existing business, or the profitability of other independent projects will lead to inferior decisions. Third, because present values are all measured in today’s dollars, you can add them up. Therefore, if you have two projects A and B, the net present value of the combined investment is
NPV(A B) NPV(A) NPV(B)
This additivity property has important implications. Suppose project B has a negative NPV. If you tack it onto project A, the joint project (A B) will have a lower NPV than A on its own. Therefore, you are unlikely to be misled into accepting a poor project (B) just because it is packaged with a good one (A). As we shall see, the alternative measures do not have this additivity property. If you are not careful, you may be tricked into deciding that a package of a good and a bad project is better than the good project on its own.
NPV Depends on Cash Flow, Not Accounting Income
Net present value depends only on the project’s cash flows and the opportunity cost of capital. But when companies report to shareholders, they do not simply
94 |
PART I Value |
show the cash flows. They also report book—that is, accounting—income and book assets; book income gets most of the immediate attention.
Financial managers sometimes use these numbers to calculate a book rate of return on a proposed investment. In other words, they look at the prospective book income as a proportion of the book value of the assets that the firm is proposing to acquire:
book income Book rate of return book assets
Cash flows and book income are often very different. For example, the accountant labels some cash outflows as capital investments and others as operating expenses.
The operating expenses are, of course, deducted immediately from each year’s income. The capital expenditures are put on the firm’s balance sheet and then depreciated according to an arbitrary schedule chosen by the accountant. The annual depreciation charge is deducted from each year’s income. Thus the book rate of return depends on which items the accountant chooses to treat as capital investments and how rapidly they are depreciated.1
Now the merits of an investment project do not depend on how accountants classify the cash flows2 and few companies these days make investment decisions just on the basis of the book rate of return. But managers know that the company’s shareholders pay considerable attention to book measures of profitability and naturally, therefore, they think (and worry) about how major projects would affect the company’s book return. Those projects that will reduce the company’s book return may be scrutinized more carefully by senior management.
You can see the dangers here. The book rate of return may not be a good measure of true profitability. It is also an average across all of the firm’s activities. The average profitability of past investments is not usually the right hurdle for new investments. Think of a firm that has been exceptionally lucky and successful. Say its average book return is 24 percent, double shareholders’ 12 percent opportunity cost of capital. Should it demand that all new investments offer 24 percent or better? Clearly not: That would mean passing up many positive-NPV opportunities with rates of return between 12 and 24 percent.
We will come back to the book rate of return in Chapter 12, when we look more closely at accounting measures of financial performance.
5.2 PAYBACK
Some companies require that the initial outlay on any project should be recoverable within a specified period. The payback period of a project is found by counting the number of years it takes before the cumulative forecasted cash flow equals the initial investment.
1This chapter’s mini-case contains simple illustrations of how book rates of return are calculated and of the difference between accounting income and project cash flow. Read the case if you wish to refresh your understanding of these topics. Better still, do the case calculations.
2Of course, the depreciation method used for tax purposes does have cash consequences which should be taken into account in calculating NPV. We cover depreciation and taxes in the next chapter.

|
CHAPTER 5 |
Why Net Present Value Leads to Better Investment Decisions Than Other Criteria |
95 |
|||||||
Consider the following three projects: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cash Flows ($) |
|
|
Payback |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Project |
|
C0 |
C1 |
C2 |
C3 |
Period (years) |
NPV at 10% |
|
|
|
A |
|
–2,000 |
500 |
500 |
5,000 |
3 |
2,624 |
|
|
|
B |
|
–2,000 |
500 |
1,800 |
0 |
2 |
–58 |
|
|
|
C |
|
–2,000 |
1,800 |
500 |
0 |
2 |
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Project A involves an initial investment of $2,000 (C0 –2,000) followed by cash inflows during the next three years. Suppose the opportunity cost of capital is 10 percent. Then project A has an NPV of $2,624:
NPV1A2 2,000 1.10500 1.105002 5,0001.103 $2,624
Project B also requires an initial investment of $2,000 but produces a cash inflow of $500 in year 1 and $1,800 in year 2. At a 10 percent opportunity cost of capital project B has an NPV of –$58:
NPV1B2 2,000 1.10500 1,8001.102 $58
The third project, C, involves the same initial outlay as the other two projects but its first-period cash flow is larger. It has an NPV of +$50.
NPV1C2 2,000 1,8001.10 1.105002 $50
The net present value rule tells us to accept projects A and C but to reject project B.
The Payback Rule
Now look at how rapidly each project pays back its initial investment. With project A you take three years to recover the $2,000 investment; with projects B and C you take only two years. If the firm used the payback rule with a cutoff period of two years, it would accept only projects B and C; if it used the payback rule with a cutoff period of three or more years, it would accept all three projects. Therefore, regardless of the choice of cutoff period, the payback rule gives answers different from the net present value rule.
You can see why payback can give misleading answers:
1.The payback rule ignores all cash flows after the cutoff date. If the cutoff date is two years, the payback rule rejects project A regardless of the size of the cash inflow in year 3.
2.The payback rule gives equal weight to all cash flows before the cutoff date. The payback rule says that projects B and C are equally attractive, but, because C’s cash inflows occur earlier, C has the higher net present value at any discount rate.
In order to use the payback rule, a firm has to decide on an appropriate cutoff date. If it uses the same cutoff regardless of project life, it will tend to accept many poor short-lived projects and reject many good long-lived ones.

96 |
PART I Value |
Some companies discount the cash flows before they compute the payback period. The discounted-payback rule asks, How many periods does the project have to last in order to make sense in terms of net present value? This modification to the payback rule surmounts the objection that equal weight is given to all flows before the cutoff date. However, the discounted-payback rule still takes no account of any cash flows after the cutoff date.
5.3 INTERNAL (OR DISCOUNTED-CASH-FLOW) RATE OF RETURN
Whereas payback and return on book are ad hoc measures, internal rate of return has a much more respectable ancestry and is recommended in many finance texts. If, therefore, we dwell more on its deficiencies, it is not because they are more numerous but because they are less obvious.
In Chapter 2 we noted that net present value could also be expressed in terms of rate of return, which would lead to the following rule: “Accept investment opportunities offering rates of return in excess of their opportunity costs of capital.” That statement, properly interpreted, is absolutely correct. However, interpretation is not always easy for long-lived investment projects.
There is no ambiguity in defining the true rate of return of an investment that generates a single payoff after one period:
payoff
Rate of return investment 1
Alternatively, we could write down the NPV of the investment and find that discount rate which makes NPV 0.
C1
NPV C0 1 discount rate 0
implies
Discount rate C1C0 1
Of course C1 is the payoff and C0 is the required investment, and so our two equations say exactly the same thing. The discount rate that makes NPV 0 is also the rate of return.
Unfortunately, there is no wholly satisfactory way of defining the true rate of return of a long-lived asset. The best available concept is the so-called discounted- cash-flow (DCF) rate of return or internal rate of return (IRR). The internal rate of return is used frequently in finance. It can be a handy measure, but, as we shall see, it can also be a misleading measure. You should, therefore, know how to calculate it and how to use it properly.
The internal rate of return is defined as the rate of discount which makes NPV0. This means that to find the IRR for an investment project lasting T years, we must solve for IRR in the following expression:
NPV C0 |
|
|
C1 |
|
C2 |
… |
|
CT |
0 |
|
IRR |
11 IRR2 2 |
|
IRR2 T |
|||||
|
1 |
|
11 |
|
|||||
