
- •Задачи.
- •§4. Обратная функция.
- •Т е о р е м а о графике обратной функции.
- •§5. S-местная функция.
- •Глава VII. Отношение.
- •§1. Отношение.
- •§2. Операции над отношениями.
- •Второй вид операций над отношениями.
- •§3. Основные свойства отношений.
- •§4. Разбиение.
- •§5. Отношение эквивалентности.
- •§6. Отношение порядка
§6. Отношение порядка
отношение
 называется отношением нестрого порядка
(нестрогим порядком), если оно транзитивно,
рефлексивно и антисимметрично, (a
называется отношением нестрого порядка
(нестрогим порядком), если оно транзитивно,
рефлексивно и антисимметрично, (a b)
b)отношение
 называется отношением совершенного
нестрогого порядка (совершенно нестрогим
порядком), если оно связано и является
отношением нестрогого порядка.
называется отношением совершенного
нестрогого порядка (совершенно нестрогим
порядком), если оно связано и является
отношением нестрогого порядка.отношение
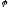 называется отношением строгого порядка
(строгим порядком), если оно транзитивно
и антирефлексивно (a<b).
называется отношением строгого порядка
(строгим порядком), если оно транзитивно
и антирефлексивно (a<b).отношение
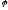 называется отношением совершенного
строгого порядка (совершенным строгим
порядком), если оно связано и является
отношением строгого порядка.
называется отношением совершенного
строгого порядка (совершенным строгим
порядком), если оно связано и является
отношением строгого порядка.
|
Порядки |
Транзи тивное |
Рефлек сивное |
Антирефлек сивное |
Антисим метричное |
Связанное |
|
Нестрогия |
+ |
+ |
|
+ |
|
|
Совершенно нестрогий |
+ |
+ |
|
+ |
+ |
|
Строгий |
+ |
|
+ |
(+) |
|
|
Совершенно строгий |
+ |
|
+ |
(+) |
+ |
Инверсия

 отношение нестрого порядка
отношение нестрого порядка и сужение
и сужение
 отношение нестрого порядка
отношение нестрого порядка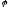
![]() <Ф,
М>
на любое подмножество А
множества М
также являются отношениями нестрогого
порядка.
<Ф,
М>
на любое подмножество А
множества М
также являются отношениями нестрогого
порядка.
Аналогичные утверждения верна для совершенного нестрогого, строгого и совершенного строгого порядка.
Примеры
x
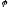
 y
y
 x<y,
(x,
y
x<y,
(x,
y  D)
D)

 -
совершенно
строгий порядок.
-
совершенно
строгий порядок.
Так
же для (x,
y
 R,
x,
y
R,
x,
y
 С,x,
y
С,x,
y
 N)
– совершенно строгий порядок
N)
– совершенно строгий порядок
x
 y
y x
x y
(x,
y
y
(x,
y
 D)
– совершенно нестрогий порядок.
D)
– совершенно нестрогий порядок.Аналогично, если x, y
 R,
С, N.
R,
С, N.
Связь между отношениями нестрогого порядка и строгого порядка на множестве М.
Если <Ф, М>- нестрогий порядок на М, то <Ф\
 ,
М>
- строгий порядок на М;
,
М>
- строгий порядок на М;Если <Ф, М>- строгий порядок на М, то <Ф

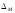 ,
М>
нестрогий порядок на М.
,
М>
нестрогий порядок на М.
Соответствие,
соотносящее произвольному нестрогому
порядку <Ф,
М>
на множестве М отношение <Ф\ ,
М
> , будет биекцией.
,
М
> , будет биекцией.
Если <Ф, М>- совершенно нестрогий порядок на М, то <Ф\
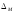 ,
М
> - совершенно строгий порядок на М.
,
М
> - совершенно строгий порядок на М.Если <Ф, М> - совершенный строгий порядок на М, то <Ф

 ,
М>
- совершенный нестрогий порядок на М.
,
М>
- совершенный нестрогий порядок на М.
Связь этих соответствий через биекцию.
Т е о р е м а (о зависимости между отношением совершенного строгого порядка на конечном множестве и перестановками над тем же множеством).
Между
множеством R
отношений совершенного строгого порядка
на конечном множестве М и множеством
 перестановок над множеством М можно
установить такое взаимное – однозначное
соответствиеf
перестановок над множеством М можно
установить такое взаимное – однозначное
соответствиеf![]() <F,
R,
<F,
R,
 >,
что (
>,
что ( )(
)( )(
)( )
[x
)
[x y
y![]() в f(
в f(
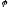 )
y
стоит правее, чем x].
)
y
стоит правее, чем x].
ЛИТЕРАТУРА
Александров П.С. Введение в общую теорию множеств и функций. М. – Л. Гостехиздат, 1948.
Айзерман М.А. и др. Логика. Автоматы. Алгоритмы. М. Физматгиз, 1963, - 556с.
Галушкин А.И. и др. Основы кибернетики. Математические основы кибернетики. М. Высшая школа. 1974. – 413с.
Глушков В.М. Синтез цифровых автоматов. М. Физматгиз, 1962. - 476с.
Поспелов. Д.А. Логические методы анализа и синтеза схем. М. Энергия, 1968. – 228с.
Успенский В.А. Лекции о вычислимых функциях. М. Физматгиз, 1960.-492с.
Чёрч А. Введение в математическую логику, т1, М., ИЛ., 1960.-484с.
Шихонович Ю.А. Введение в современную математику. М. 1965. – 376с.

