§4. Разбиение.

Система M множеств называется разбиением множества М, если она удовлетворяют условиям М:

1. (X M)[XM].

2. (X M)[X0].

3. (X M) (Y M)[XYXY=0].

4. M.

Элементы XM называется классами разбиения. Разбиение M множества М называется поэлементным, если каждый класс разбиения M является одноэлементным множеством.

Разбиение M множества называется цельным, если M ={М}.

Целое и поэлементное разбиение множества М называется тривиальными разбиениями множества М, остальные разбиения, если существуют – нейтральные разбиения.

Примеры 1. а) M 0 является тривиальным разбиением множества М=0. (но не целое разбиение)

б) М{а} имеет единственное разбиениеM {M}= {{а}}. Это разбиение целое и поэлементное.

в) М{a, b} имеет два разбиения: M

{М} – целое разбиение, M

{{a}, {b}} - поэлементное разбиение.

M

M

4)M{a,b,c} – имеет 5 разбиений.

M₃ M₅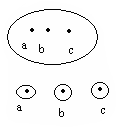

M

M M₄

5) система групп данного курса является разбиением множества студентов курса.

6) A - множество четных натуральных чисел N.

А- множество нечетных натуральных чиселN.

M {A

, А}

Является разбиением множества N.

7) Пусть C - множество n – значных натуральных чисел (n= 1, 2, 3, …). Тогда система M (C

, С, …) – является разбиением множества N.

8) f:XY - сюръективное отображение.

Система M полных преобразований f({y}), взятых для всех элементов множества Y, является разбиением множества X, разбиение на классы преобразовав относительно f.

§5. Отношение эквивалентности.

Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. ab или a~ b (1) говорят, что a и b эквивалентны (по отношению ) или а эквивалентноb. Инверсия f отношение эквивалентности и сужениеотношение эквивалентности<Ф, М> на любое подмножество А множества М является отношением эквивалентности.

Примеры отношений эквивалентности:

1. полное отношение <М, М> на множестве М.

2. пустое отношение опри М=0.

3. Отношение равенства Ена множестве М является отношением эквивалентности

4. Отношение «быть в одной группе».

5. f: XY – отображение . xx f(x)= f(x).

6. Отношение «иметь одинаковую фамилию» на множестве людей Земли.

Отношение на множестве М и разбиениеM множества М сопряжены, если для любых элементов x и y множества М xy тогда и только тогда, когда x и y принадлежат к одному и тому же классу разбиения M, т.е. если (xМ)( yМ){ xy (А M)[x А&yA]}.

Когда иM сопряжены, будем говорить: сопряжено сM или M сопряжено с .

Пример таких сопряжений:

1. отношение равенства Е на множестве М и поэлементное разбиение множества М сопряжены.

2. Отношение «быть в одной группе» на множестве студентов курса и разбиение на группы того же множества сопряжены.

3. Отношение «иметь одинаковую фамилию» на множестве людей Земли и разбиение того же множества на классы однофамильцев сопряжены.

4. Естественно возникает вопрос: для любого ли отношения существует сопряжение с ним разбиение? Может ли существовать несколько разбиений, сопряженных с данными отношениями?

Ответ на 2- ой вопрос дает

Т е о р е м а 1 (о единственности разбиения, сопряженного с данными отношениями)

Если два разбиения множества М сопряжены с одним и тем же отношением на множестве М, то они совпадают. Другими словами: разбиение, сопряженное с данным отношением, единственно.

Т е о р е м а 2 (теорема об отношении, сопряженной с некоторыми разбиениями)

Если отношение на множестве М сопряжено с каким-нибудь разбиением множества М, то- отношение эквивалентности.

Итак, разбиение, сопряженное с отношением , существует только в том случае, когда- отношение эквивалентности. Но для любого ли отношения эквивалентности существует сопряжение с ним разбиение?

Ответ (положительный) дает Теорема 3.

Т е о р е м а 3. (теорема о существовании разбиения, сопряженного данным отношением эквивалентности).

Для любого отношения эквивалентности сопряженное с ним разбиение множества М.

Легко доказать, что для любого разбиения множества М существует единственное сопряженное с ним отношение на множестве М (причем, в силу т.2) это отношение является отношением эквивалентности.

Таким образом, соответствие, соотносящее произвольному отношению эквивалентности на множестве М является биекцией (взаимно – однозначных соответствий) между системой отношений эквивалентности на множестве М и системой разбиений множества М.

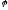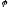Разбиение множества М, сопряженное с отношением и обозначается через, которое существует в том и только в том случае, когда- отношение эквивалентности на множестве М.

Если - отношение эквивалентности на множестве М, то

xy (

А)[xA&yA].