
- •Задачи.
- •§4. Обратная функция.
- •Т е о р е м а о графике обратной функции.
- •§5. S-местная функция.
- •Глава VII. Отношение.
- •§1. Отношение.
- •§2. Операции над отношениями.
- •Второй вид операций над отношениями.
- •§3. Основные свойства отношений.
- •§4. Разбиение.
- •§5. Отношение эквивалентности.
- •§6. Отношение порядка
§2. Операции над отношениями.
I-ый вид операций.
На отношения переносятся общие операции над множествами.
Пусть
 ,
,
а)Соединением
(объединением)
отношений
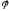 и
и называется отношение на множестве М,
график которого равен соединению
графиков отношений
называется отношение на множестве М,
график которого равен соединению
графиков отношений и
и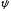 .
.
 (9).
(9).
Если
известно, что
 и
и - отношения на одном и том же множестве,
то определение (9) можно записать так:
- отношения на одном и том же множестве,
то определение (9) можно записать так: (10)
(10)
Очевидно,
 (11).
(11).
б)
Пересечением
отношений
 и
и называют отношение на множестве М,
график которого равен пересечению
графиков отношений
называют отношение на множестве М,
график которого равен пересечению
графиков отношений и
и .
.
 (12).
(12).
Очевидно,
 (13).
(13).
в)
Разностью
отношений
 и
и называют отношение на множестве М,
график которого равен пересечению
графиков отношений
называют отношение на множестве М,
график которого равен пересечению
графиков отношений и
и .
.
 (14).
(14).
Очевидно,
 (15).
(15).
Для отношений большое значение имеет частный случай разности – операция дополнения.
г)
Дополнением
к отношению
 называют
отношение на множестве М, график которого
равен дополнению графика отношения
называют
отношение на множестве М, график которого
равен дополнению графика отношения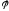 до М2.
до М2.
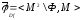 (16).
(16).
Очевидно,
 (17).
(17).
Если
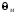 - полное отношение на множестве М, то
для любого отношения
- полное отношение на множестве М, то
для любого отношения на М
на М (18)
(18)
С
другой стороны, очевидно  (19).
(19).
На
отношение (на одном и том же множестве)
автоматически переносятся все «тождества
с множествами». Например,![]()
Второй вид операций над отношениями.
На отношения переносятся операции над графиками.
I)
Инверсией
отношения
 называют отношение на множестве М,
график которого есть инверсия графика
отношения
называют отношение на множестве М,
график которого есть инверсия графика
отношения ,
т.е.
,
т.е.
 (20).
(20).
Очевидно,
 (21).
(21).
Например,
отношение
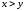 наD
является инверсией отношения
наD
является инверсией отношения
 наD.
наD.
 .
.
II)
Композицией
отношений
 ,
,
 называют отношение на множестве М,
график которого равен композиции
графиков отношений
называют отношение на множестве М,
график которого равен композиции
графиков отношений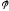 и
и .
.
 (22).
(22).
Очевидно,
 (23).
(23).
III)
На отношения (на одном и том же множестве)
автоматически переносятся все «тождества
с графиками». Например, 
Под
композицией
 отношений
отношений на одном и том же множестве М понимается
результат последовательного попарного
компонирования отношений
на одном и том же множестве М понимается
результат последовательного попарного
компонирования отношений при любой расстановке скобок.
при любой расстановке скобок.
Подчеркнём, что все операции над отношениями применяются к отношениям с одной и той же областью задания и в результате применения операции снова получается отношение с той же областью задания.
Отметим,
что для любого отношения
 на множестве М
на множестве М (24)
(24)
Будем
говорить, что отношение
 влечёт (или имплицирует) отношение
влечёт (или имплицирует) отношение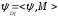 и будем писать
и будем писать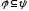 ,
если
,
если :
:
 (25).
(25).
Очевидно,
 (26)
(26)
Введём «операцию», меняющую область задания отношений.
Пусть
 - отношение на множестве М и
- отношение на множестве М и .Сужением
отношения
.Сужением
отношения
 на множество А
называется и через
на множество А
называется и через
 обозначается отношение вида
обозначается отношение вида (27)
(27)
Т.е.
 (28).
(28).
Например,
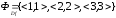
 ,
,
 ,
, ,
, .
.
§3. Основные свойства отношений.
А)
Отношение
 называетсярефлексивным,
если
называетсярефлексивным,
если
 (1).
(1).
Очевидно,
отношение 
 рефлексивно
тогда и только тогда, когда
рефлексивно
тогда и только тогда, когда
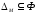 (2),
т.е. все точки диагонали принадлежат
графику отношения.
(2),
т.е. все точки диагонали принадлежат
графику отношения.
Отношение
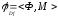 называется антирефлексивным,
если
называется антирефлексивным,
если
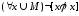 (3)
(3)
Или
 (4).
(4).
Очевидно,
отношение
 антирефлексивно тогда и только тогда,
когда
антирефлексивно тогда и только тогда,
когда (5).
(5).
Т.е когда ни одна точка диагонали не принадлежит графику отношений.


График
рассматриваемого отношения
В)
Отношение
 называетсясимметричным,
если
называетсясимметричным,
если
 (6).
(6).
(область
значений переменных
 ,
кванторы опущены).
,
кванторы опущены).
Очевидно,
отношение
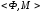 симметрично тогда и только тогда, когда
его график
симметрично тогда и только тогда, когда
его график симметричен или
симметричен или (7).
(7).

Для
дальнейшего заметим, что определение
(6) равносильно, как это ни странно на
первый взгляд, определению
 (8).
(8).
Отношение
 называетсяантисимметричным,
если
называетсяантисимметричным,
если
 (9).
(9).
Или
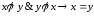 (10).
(10).
Из
(10) следует, что отношение
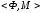 антисимметрично
антисимметрично ,
когда
,
когда (11).
(11).
Определение
(9) можно представить по-другому
 (12).
(12).
С)
Отношение
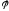 называется связанным,
если
называется связанным,
если
 (13), т.е.
(13), т.е.
 (14).
(14).
D)
Отношение
 называется транзитивным,
если
называется транзитивным,
если
 (15), т.е. отношение
(15), т.е. отношение
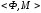 транзитивно
транзитивно ,
когда
,
когда (16).
(16).
Отношение
 транзитивно
транзитивно ,
когда
,
когда (17).
(17).
Введённые выше 6 свойств будем называть основными свойствами отношений.
Очевидно,
Если отношение
 обладает каким-то из основных свойств,
то его инверсия
обладает каким-то из основных свойств,
то его инверсия также обладает этим свойством.
также обладает этим свойством.Если отношение
 обладает каким-то из основных свойств
и
обладает каким-то из основных свойств
и ,
то и сужение
,
то и сужение отношения
отношения на множество А также обладает этим
свойством.
на множество А также обладает этим
свойством.
