Глава VII. Отношение.

§1. Отношение.

Слово «отношение» встречается в математике довольно часто (например, в школе говорят 3<5).

Однако на это отношение «меньше» можно взглянуть со следующей, несколько новой стороны: определить отношение «меньше» для действительных чисел – это значит выделить некоторый график , в который войдут те и только те пары, компоненты которых находятся между собой в нужном нам отношении. Отношение «меньше» для действительных чисел полностью характеризуется,

во-первых, множеством D,

во-вторых, графиком .

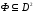Легко видеть, что аналогично можно истолковать слово «отношение» для отношения подобия треугольников, для отношения параллельности прямых и т.п. Что же такое «отношение»? Что следует называть отношением?

Отношение – это пара множеств (Ф,М), первая (Ф) компонента которой является подмножеством квадрата второй компоненты (М):

(1)

где .

- есть график отношения,

- область задания отношения.

Отношение с областью задания М называетсяотношением на множестве М.

Иногда говорят, что отношение задано на М.

Если , то будем писатьb (2)

и говорить: «элементы a и b находятся в отношении »;

или элемент a находится в отношении к элементуb

(или «пара находится в отношении»;

или «пара удовлетворяет отношению»;

или «для пары выполнено отношение»).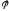

Если a, b – элементы множества М, то b – является (истинным или ложным) высказыванием.

Если a или b является переменной с областью значений М, то 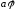b является (одноместной или двухместной) высказывательной формой.

Отношения обозначают строчными греческими () буквами;

Графики отношений – прописными греческими буквами.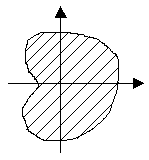

Пример 1: У

.

<Ф,D> отношение на D.

Х

Любое подмножество является графиком некоторого отношения наD: .

Пример 2: У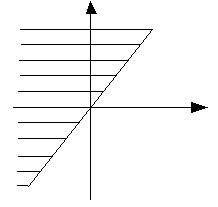

график Х Отношение

отношения есть отношение «меньше» на D.

x<y

Пример 3:

есть отношение наN.

есть отношение на{1,2,3}.

График Ф.

Если Y, M, M> - соответствие между множествами M и М, то

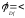Y, M> отношение на М (и обратно).

Какая разница между понятиями

соответствие и отношение?

Соответствие имеет направление от области отправления к области прибытия ( ), первой компоненте пары a соответствует вторая компонента пары b. (Элементы a и b не равноправны); отношение характеризует свойство пар из М².

Способ задания отношения

при помощи высказывательных форм.

Пусть A – двухместная высказывательная форма с переменными x и y, область значений переменных x и y – множество А и .

Тогда фраза:

Зададим на М отношение 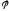: A (3)

или, короче, выражение A (4)

определяет отношение на множестве М с графиком

Очевидно, для так определённого отношения 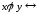A (x,y)&(5)

Если 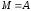, то вместо(4) пишем(6).

Пример:

или

график

этого

отношения

Если A (x) – одноместная высказывательная форма, область значений переменной х – множество А и , то под (7) A (x,y) 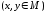понимается отношение на М с графиком.

Аналогично,

(8)

означает отношение на М с графиком .

Отношение

называется полным или , т.е. если

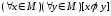
Очевидно, 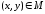есть полное отношение на М.

Отношение называетсяпустым, если , т.е. если.

Очевидно, отношение есть пустое отношение на М.

Пустое отношение будем обозначать .

Отношение

называется отношением равенства, если , т.е.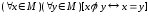

Очевидно, отношение есть отношение

равенства на М.

Отношение равенства .

Отношение называетсяотношением неравенства, если , т.е. если.

Очевидно, отношение есть отношение

неравенства на М.

Пример: .