
- •Задачи.
- •§4. Обратная функция.
- •Т е о р е м а о графике обратной функции.
- •§5. S-местная функция.
- •Глава VII. Отношение.
- •§1. Отношение.
- •§2. Операции над отношениями.
- •Второй вид операций над отношениями.
- •§3. Основные свойства отношений.
- •§4. Разбиение.
- •§5. Отношение эквивалентности.
- •§6. Отношение порядка
Т е о р е м а о графике обратной функции.
Если
g <
Y,Y,X>
является обратной для
<
Y,Y,X>
является обратной для
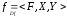 ,
то:
,
то:
1) Y =H-1, где H – график сужения h функции f на область значений пр2 Y функции g.
g=h-1.
Д о к а з а т е л ь с т в о: Поскольку h-1=< H-1,Y,X>. Второе утверждение вытекает из первого. Докажем первое утверждение. По определению сужения
H=F∩( пр2 Y ×Y) (15)
откуда
H-1=F-1∩( Y ×пр2 Y) (16)
Т.е. в силу (16) нужно доказать
Y =F-1∩( Y ×пр2 Y) (17)
Пусть
 Y.
По (8)
Y.
По (8)
 .
Поскольку
Y
.
Поскольку
Y
 ,
,
 ,
, Y.
Y.
Следовательно,
 Y,
Y,
 Y).
Y).
Пусть,
обратно,
 Y).
Y).
Тогда
 и
и

 Y.
Y.
Следовательно,
 и
и Y.
Y.
По
определению проекции множества существует
такое с,
что
 Y.
Из (8)
Y.
Из (8)
 .
В силу функциональности графикаF,
a=c.
Значит,
.
В силу функциональности графикаF,
a=c.
Значит,
 Y.
Y.
Пример 1:
У


 - инверсияf(x)
(не есть функция)
- инверсияf(x)
(не есть функция)
Х
Пример
2: 


 -
инъекция.
-
инъекция.
 - функция
- функция
У 

Х
§5. S-местная функция.
Пусть
 .
.
Функция f называется S-местной (двух, трёх и т.д.), если её область отправления состоит из …… длины S.
 (1)
(1)
Обычно так записывают S – местную функцию.
Для
любого множества М произвольная функция
типа
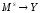
 является примеромS-местной
функции.
является примеромS-местной
функции.
Функции
типа
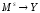 называют иногдаS-местными
функциями типа
называют иногдаS-местными
функциями типа
 .
Употребляя этот термин, следует помнить,
что любая S-местная
функция типа
.
Употребляя этот термин, следует помнить,
что любая S-местная
функция типа
 является (при
является (при )S-местной
функцией, но не является функцией типа
)S-местной
функцией, но не является функцией типа
 .
.
Нульместная
функция типа
 имеет либо вид
имеет либо вид ,
где
,
где ,
либо вид
,
либо вид .
.
Как
и функции типа
 ,S-местные
функции типа
,S-местные
функции типа
 можно задавать при помощичисловых
форм или чисел.
Пусть, например,
можно задавать при помощичисловых
форм или чисел.
Пусть, например,
 -S-местная
числовая форма с числовыми переменными
-S-местная
числовая форма с числовыми переменными
 .
.
Тогда
выражение  (2) обозначаетS-местную
функцию типа
(2) обозначаетS-местную
функцию типа
 с графиком
с графиком .
.
Аналогичный
смысл имеет выражение
 (3).
(3).
Задавая
ту же функцию (2), оно одновременно вводит
для неё имя f.
Выражение
 (4) задаётS-местную
функцию типа
(4) задаётS-местную
функцию типа
 ,
однако чтобы эта функция была вполне
определена, нужно ещё фиксировать тем
или иным способом (например, перенумеровав)
порядок переменных в формеU.
,
однако чтобы эта функция была вполне
определена, нужно ещё фиксировать тем
или иным способом (например, перенумеровав)
порядок переменных в формеU.
Пример
1:
Выражения
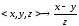 (5)
(5)
и
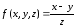 (6)
(6)
задают
одну и ту же функцию типа
 .
Если в форме
.
Если в форме порядком переменных считать алфавитный
порядок, то выражение
порядком переменных считать алфавитный
порядок, то выражение (7)
(7)
задаёт ту же функцию (5).
Если
же в этой форме переменных считать
обратный порядок
 ,
то значение функции (7) на тройке <2,3,5>
будет уже равно
,
то значение функции (7) на тройке <2,3,5>
будет уже равно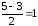 ,
а не
,
а не .
.
Пусть
S
– натуральное число. Отображение
множества
 в
в называетсяS-местной
(алгебраической) операцией на М.
S-местная
операция на М – это всё равно, что всюду
определённая S-местная
функция типа
называетсяS-местной
(алгебраической) операцией на М.
S-местная
операция на М – это всё равно, что всюду
определённая S-местная
функция типа
 .
.
Одноместную операцию на М называют унарной, (unus – один).
Двухместную операцию на М называют бинарной, (bini – два).
Трёхместную операцию на М называют тернарной.
Пример
2: Сложение
и умножение являются двухместными
операциями на каждом из множеств N,
C,
R,
D,
K.
Разумеется, сложение на N
и сложение на C
являются разными операциями, т.к. сложение
на N
– это тройка вида <
Y
 ,
а сложение на С – это тройка вида
,
а сложение на С – это тройка вида .
С другой стороны,Y
.
С другой стороны,Y
 .
.
Пример
3:
Вычитание является двухместной операцией
на каждом из множеств C,
R,
D,
K,
но не является операцией на N,
т.к. при
 разность
разность вN
не определена.
вN
не определена.
Пример
4:
Деление не является операцией ни на
одном из множеств R,
D,
K
ввиду невозможности деления на 0, однако
деление является двухместной операцией
на каждом из множеств 
Пример
5: Для
любого множества М
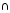 ,
, ,
\ можно считать двухместными операциями
на
,
\ можно считать двухместными операциями
на ,
операцию дополнения – одноместной
операцией на
,
операцию дополнения – одноместной
операцией на .
.
Пример
6:
Для любого множества М композицию
графиков можно считать двухместной
операцией на
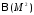 ,
а инверсию графика – одноместной
операцией на
,
а инверсию графика – одноместной
операцией на .
.
