
- •Задачи.
- •§4. Обратная функция.
- •Т е о р е м а о графике обратной функции.
- •§5. S-местная функция.
- •Глава VII. Отношение.
- •§1. Отношение.
- •§2. Операции над отношениями.
- •Второй вид операций над отношениями.
- •§3. Основные свойства отношений.
- •§4. Разбиение.
- •§5. Отношение эквивалентности.
- •§6. Отношение порядка
Примеры:
1) 


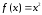
 Эти
выражения задают одну и ту же
Эти
выражения задают одну и ту же
 функцию
типа
функцию
типа





2) 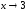

 Задают одну и ту же константную
Задают одну и ту же константную
 функцию типа
функцию типа
2=3 

3)  (x
(x [2,3])
[2,3]) 
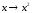 (2
(2 x
x 3)
Задают
сужение
3)
Задают
сужение
 (x
(x [2,3])
функции
[2,3])
функции
 на множество
на множество
 (2
(2 x
x 3)
3) 

4)  Является
нигде не определённой функцией типа
Является
нигде не определённой функцией типа

5) 
Тождественная
функция типа


6)
Функция
 тождественно на (0;+∞), но не является
тождественной функцией.
тождественно на (0;+∞), но не является
тождественной функцией.
(стрелочка означает, что её «конец», т.е. точка <0,0> не принадлежит графику).
(иногда
обозначают координату где функция не
существует 
 )
)
7)Функция
 константна на (0;+∞) и (-∞,0), но не является
константной функцией:
константна на (0;+∞) и (-∞,0), но не является
константной функцией:

Если f – функция типа
 ,
тоf(x),
f(2x),
f(3x-5),
f(sin
x)
– числовые формы.
,
тоf(x),
f(2x),
f(3x-5),
f(sin
x)
– числовые формы.
Поэтому выражения
 задают
функцию
типа
задают
функцию
типа


Иногда
функции типа
 на разных участках области определения
приходится задавать разнымичисловыми
формами.
на разных участках области определения
приходится задавать разнымичисловыми
формами.
Пусть A1,…,An- попарно не пересекающиеся подмножества множества D;
U1(x),…,Un(x) – одноместные числовые формы с числовой переменной x.
Тогда выражения

(49)
 (50)
(50)
 (51)
(51)
обозначают
функцию типа
 с графиком
с графиком ,
где
,
где .
.
Задание функции по схемам (49)-(51) называется кусочным заданием.
Пример:
9) 
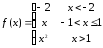
Функция на [-2,-1] не определена.
Пусть
f
и g
функции типа
 .
Согласно теореме о значении композиции,
композиция
.
Согласно теореме о значении композиции,
композиция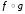 функцийf
и g
может
быть задана формой
функцийf
и g
может
быть задана формой
 .
.
Т.о., выражения
 задают функцию
задают функцию
Это справедливо и для большого количества функций
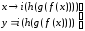 задают
функцию
задают
функцию

Пример:
10)
Функция
 композиция
композиция
 функций
функций

В тех же обозначениях функция
 равна
равна ,
а функция
,
а функция равна
равна .
.
Указанный
способ задания функций типа
 годится и для общего случая.
годится и для общего случая.
Пусть
 ,
, - одноместная
форма, значениями которой являются
элементы множества
- одноместная
форма, значениями которой являются
элементы множества
 .
.
Тогда
выражения
 обозначают
функцию типа
обозначают
функцию типа с графиком
с графиком .
.
Задачи.
Чему равно число нижеуказанных функций типа
 ,
если
,
если
 ,
,
 :
:
а)
отображений? 
 .
.
§4. Обратная функция.
Рассмотрим
предварительно некоторые свойства
инверсии
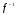 .
.
Пусть
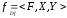 - произвольная инъекция. Тогда в силу
критерия функциональности инверсии
(§1)
- произвольная инъекция. Тогда в силу
критерия функциональности инверсии
(§1) - функция.
- функция.
Отметим
три свойства функции
 :
:
1)  -
инъекция. (1)
-
инъекция. (1)
2)  - тождественно на пр1
- тождественно на пр1
 (2)
(2)
3)  -
тождественно
на
пр2
-
тождественно
на
пр2
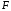 (3)
(3)
Д о к а ж е м (2):
Пусть
 пр1
пр1
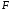 .
Требуется доказать, что
.
Требуется доказать, что
 или в силу теоремы о значении композиции
или в силу теоремы о значении композиции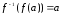 .
Т.к.
.
Т.к. пр1
пр1
 ,
то
,
то
 .
.
Пусть
 ,
т.е.
,
т.е. .
Значит
.
Значит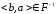 .
Следовательно,
.
Следовательно, .
Итак,
.
Итак, .
.
(3) доказывается аналогично.
Кроме
того, поскольку
 и пр2
и пр2
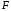 =
пр1
=
пр1
 ,
то (3) следует прямо из (2).
,
то (3) следует прямо из (2).
Пусть
 - произвольная функция. Обязательно ли
существует также функцияg
типа
- произвольная функция. Обязательно ли
существует также функцияg
типа
 ,
что
,
что тождественна на пр1
тождественна на пр1
 (4)
(4)
Легко видеть, что требуемая функция g существует тогда и только тогда, когда f – инъекция.
На
вопрос: Обязательно ли существует также
функция g
типа
 ,
что
,
что тождественна на пр2
тождественна на пр2
 (5) можно ответить: в отличие от (4) требуемая
функция g,
существует всегда, для любой функции
f.
(5) можно ответить: в отличие от (4) требуемая
функция g,
существует всегда, для любой функции
f.
Из
этих двух возможностей (4) и (5) ответим
на вопрос, какую функцию g
типа
 стоит называть обратной дляf
функций.
стоит называть обратной дляf
функций.
Пусть
f
– произвольная функция типа
 .
Функцияg
типа
.
Функцияg
типа
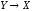 называетсяобратной
для функции f,
если:
называетсяобратной
для функции f,
если:
во-первых, её область определения равна области значений функции f;
во-вторых,
функция
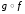 тождественна на области значений функцииf.
тождественна на области значений функцииf.
Итак,
gDf=<Y,Y,X>
является обратной для
 ,
если выполняется два условия: пр1
Y
=пр2F (6)
,
если выполняется два условия: пр1
Y
=пр2F (6)
 тождественно на пр2F
(7).
тождественно на пр2F
(7).
Отсюда вытекают следующие свойства:
Y
 (8)
(8)
пр2
Y
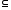 пр1
F (9)
пр1
F (9)
 тождественна на пр2
Y
(10)
тождественна на пр2
Y
(10)
g – инъекция (11).
Д о к а ж е м, например, (10).
Пусть
a пр2
Y.
По
определению проекции множества существует
такое b,
что <b,a>
пр2
Y.
По
определению проекции множества существует
такое b,
что <b,a> Y.
По (8) <b,a>
Y.
По (8) <b,a> F-1
и <a,b>
F-1
и <a,b> F.
Из <a,b>
F.
Из <a,b> F
следует
f(a)=b.
F
следует
f(a)=b.
Из
<b,a> Y
следует
g(b)=a.
Следовательно,
Y
следует
g(b)=a.
Следовательно,
 .
.
Остальные доказательства – аналогично.
В математической практике «обратность» обратной функции чаще всего используется в виде следующих простых свойств:
 (12)
(12)
 &пр2
Y
&пр2
Y
 (13)
(13)
Эти свойства являются фактически переформулировкой свойств (7), (10).
Однако утверждение всегда

 (14)
(14)
в общем случае не верно.
Например,
 .
.
Пусть
график функции f
типа
 задаётся так:
задаётся так:

![]()
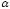

- график функции g.
Тогда
функция g
является
обратной для функции f
и
 ,
но не верно, что
,
но не верно, что .
.
Рассмотрим вопросы существования и единственности обратной функции.
Выше, доказывая, что для любой функции f существует функция g со свойством (5), мы доказали фактически, что для любой функции f существует обратная функция, т.к. построенная там функция …… областью определения пр2F, а (5) совпадает с (7).
Функция, обратная для функции f, единственна тогда и только тогда, когда f – инъекция.
Если
f
–
инъекция, то её единственной обратной
функцией g
является функция
 .
.
Если f – не инъективна, то у неё обязательно существует больше одной обратной функции, причём различные её обратные функции отличаются областью значений.
Для
того чтобы задать функцию g,
обратную для функции
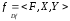 ,
достаточно задать такое подмножество
,
достаточно задать такое подмножество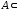 пр1F,
которое для каждого
пр1F,
которое для каждого
 пр2F
содержит один и только один прообраз
пр2F
содержит один и только один прообраз
 пр1F
относительно
f.
Тогда пр2
Y
=A.
g
пр1F
относительно
f.
Тогда пр2
Y
=A.
g <
Y,Y,X>.
<
Y,Y,X>.
