§3. Теоремы о композициях.

Рассмотрим операцию композиции.

1. Композиция функций есть функция.

2. Композиция инъекций есть инъекция.

При условии совпадения область прибытия первой композиционной функции и области отправления второй компонируемой функции:

3. Композиция отображения есть отображение.

4. Композиция сюръекции есть сюръекция.

5. композиция биекции есть биекция.

Теорема о значении композиции

Теорема 1. Если f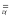 <F, X, Y> , g <G, Z, U> - произвольные функции, то имеет место (теорема о значении композиции): Для любых f и g (fg)(x) g(f(x)) (21).

(область значений переменной x является область отправления функции f).

Доказательство: Пусть fg = <FG, X, U>, aX и ! (fg)(а).

Положим (fg)(а)

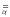b. Согласно (9) (f(x)=y<x, y>F) можем записать:

<a, b>FY.

Следовательно, существует такое с, что

<a, c> F (22)

<c, b>Y. (23)

Из (22) и (9) f(a)=c. Из (23) и (9) g(с)=b. Значит g(f(a))= g(c)=b.

Пусть, обратно, аX и ! g(f(a)). Из ! g(f(a)) следует !f(a). Положим f(a)

c.

Следовательно, g(c) = b. Отсюда и из (9) получим (22), (23).

Из (22), (23) <a, b> FY. По (12) (fg)(a)=b.

Теорема о значении композиции верна для любого (конечного) числа функций: (f₁ f₂… f_n) (x) f_n(…( f₂( f₁(x))…). (24)

Для доказательства биективности соответствий часто бывает полезной.

Теорема 2. Теорема о тождественных композициях.

Пусть f функция типа XY, g функция типа YX.

Если обе композиции: fg и gf - является тождественными функциями, то f – биекция, g – биекция и q=f.

Доказательство: Пусть f = <F, X, Y>, g = <Y, Y, X>

Тогда fg= <FY, X, X>, gf = <YF, Y, Y>. По условию fg=I_x, gf=I_y, следовательно, FY =

_x (25)

YF=

_y. (26)

1. ….. fg – биекция, f – инъективное отображение и g – сюръекция. Аналогично g – инъективное отображение и f – сюръекция. Значит, f и g – биекция.

2. Рассмотрим теперь f= <F, Y, X>.

Надо доказать, что g= f, т.е., что Y=F. Пусть <a, b>Y. Поскольку bX и f – всегда определена, !f(b).

Положим f(b) c. Согласно (9) <b, c>F. Значит, <a, c>YF.

Из (26) с=а. следовательно, <b, a> F и <a, b>F. Пусть, обратно, <a,b>F. Тогда <b, a> F. Поскольку аY и g всегда определена, !g(a). Положим g(a)

c. По (9) <a, c> Y.

Значит, <b, c>FY . Из (25) с=b. Следовательно, <a, b> Y. Теорема доказана.

Так как для произвольных f, g g=f g=f (27)

то если f и g удовлетворяют условиям теоремы о тождественных композициях, то не только g=f, но и f=g.

Сужение любой функции f на любое множество A есть функция.

Для любых функций f <F, X, Y> и для любого множества А:

(xA)[ !f_A (x) xA & !f(x) & f_A(x) = f(x)] (28)

(xA)[ !f_A(x)!f(x)] (29).

Есть функция g является продолжением функции f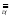<F, X, Y>, то

(xX)[!f(x)!g(x) & g(x)=f(x)] (30).

Рассмотрим функцию типа DD. (D – множество действительных чисел). Функции типа DD чаще всего задаются при помощи числовых форм.

Пусть U(x) – одноместная числовая форма с числовой переменной x. Обозначим через xU(x) (31)

Функцию типа DD с графиком F: F

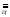
{<x, y>D| y=U(x)}.

Очевидно (31) и yU(y). Задают одну и ту же функцию:

xU(x) = yU(y).

В нашей литературе вместо (31) чаще пишут y=U(x) (32)

или, вводя для функции (31) индивидуальное имя, f(x) = U(x) (33)

Буква x в (32) называется независимой переменной или аргументом, а буква y- зависимой переменной.

Задавая функцию (31) равенством вида (32), можно как независимую, так и зависимую переменную обозначать любой буквой. Заданная функция от обозначения переменной конечно, не зависит:

z=U(x) (34)

z=U(g) (35)

z=U(y) (36)

(34) - (36) задают одну и ту же функцию.

Пусть А – множество. Тогда через xU(x) (xA) (37)

и, соответственно, y=U(x) (xA) (38)

f(x)=U(x) (xA) (39)

U(x) (xA) (40)

обозначают сужение функции (31) на А.

Подобно заданного через числовые формы, можно задавать функции типа DD при помощи чисел.

Если bD, то выражение xb (41)

Обозначает константную функцию <D{b}, D, D>. Или по-другому:

y=b (42)

f(x)=b (43)

b (44)

Равенство (42) содержит зависимую переменную (y) и не содержит независимой переменной.

Равенство (43) отличается от равенства (42) тем, что задавая функцию при помощи (43), мы одновременно вводим для неё f.

Сужение функции (41) на А обозначается, соответственно, через

xb (xA) (45)

y=b (xA) (46)

f(x)=b (xA) (47)

b (xA) (48).

42