
- •Глава V. Соответствие.
- •§1. Соответствие.
- •Операции композиции соответствий
- •§2. Основные свойства соответствия
- •Примеры I-V.
- •Глава VI. Функция.
- •§1. Функция.
- •§2. Основные свойства функции.
- •§3. Теоремы о композициях.
- •Теорема о значении композиции
- •Теорема 2. Теорема о тождественных композициях.
§2. Основные свойства функции.
Функция f
 <F,
X,
Y>
называется нигде не определенной, если
F=0.
Условимся говорит, что функция f
<F,
X,
Y>
называется нигде не определенной, если
F=0.
Условимся говорит, что функция f <F,
X,
Y>
определена
на множестве
А, если А
<F,
X,
Y>
определена
на множестве
А, если А пр
пр F,
т.е. если (
F,
т.е. если ( x
x А)[!F(x)].
В частности, очевидно, любая функция а
определена на 0.
А)[!F(x)].
В частности, очевидно, любая функция а
определена на 0.Функция f
 <F,
X,
Y>
называется тождественной,
если Y=X
и F=
<F,
X,
Y>
называется тождественной,
если Y=X
и F= ,
т.е.I
,
т.е.I =
f
=<
=
f
=<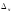 ,x,
x>
- тождественная функция.
,x,
x>
- тождественная функция.
Условимся
говорить, что функция f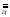 <F,
X,
Y>
тождественна на множестве А, если
<F,
X,
Y>
тождественна на множестве А, если

 F,
т.е. если (
F,
т.е. если (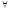 x
x A)[f(x)=x].
A)[f(x)=x].
Функция
I тождественна на всей области отправления
X.
Очевидно, любая функция тождественна
0.
тождественна на всей области отправления
X.
Очевидно, любая функция тождественна
0.
III.
Функция
f <F,
X,
Y>
называется константной,
если существует такой элемент b
<F,
X,
Y>
называется константной,
если существует такой элемент b Y,
что F=X
Y,
что F=X {b}.
{b}.
Условимся
говорить, что функция f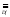 <F,
X,
Y>
константа на множестве А,
<F,
X,
Y>
константа на множестве А,
если
( y
y Y)[A
Y)[A {y}
{y} F]т.е.
F]т.е.
если
( y
y Y)
(
Y)
( x
x A)[f(x)=y].
A)[f(x)=y].
IV.
Функция f <F,
X,
Y>
тогда и только тогда является всюду
определенной, когда (
<F,
X,
Y>
тогда и только тогда является всюду
определенной, когда ( x
x X)[!
f(x)].
X)[!
f(x)].
Согласно
введенной выше терминологии, всюду
определенная функция f <F,
X,
Y>
определена на X.
<F,
X,
Y>
определена на X.
Всюду
определенная функция называется также
отображением, а всюду определенную
функцию типа X Y
– отображением множества X
в множество Y.
Y
– отображением множества X
в множество Y.
Тождественная
функция I является, очевидно, отображением.
является, очевидно, отображением.
Отображение
I называется так же тождественным
отображением
множества X
на себя.
называется так же тождественным
отображением
множества X
на себя.
Константная функция так же, очевидно, является отображением (константное множество).
Если функция f является отображением, то значение f(a) (функции f на а) называется так же образом элемента а при отображении f.
V.
Функция
f <F,
X,
Y>
тогда и только тогда сюръективна,
когда (
<F,
X,
Y>
тогда и только тогда сюръективна,
когда (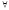 y
y Y)(
Y)(
 x
x X)[f(x)=y].
X)[f(x)=y].
Сюръективную функцию мы будем называть сюръекцией.
Термины «всюду определенная сюръекция», «сюръективное отображение» означает функцию, одновременно всюду определенную и сюръективную.
Сюръективное
отображение типа X Y
называют так же отображением
множества X
на Y.
Y
называют так же отображением
множества X
на Y.
Тождественное
отображение I является сюръекцией.
является сюръекцией.
VI.
Функция f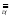 <F,
X,
Y>
тогда и только тогда инъективна,
когда
<F,
X,
Y>
тогда и только тогда инъективна,
когда
x
 x
x
 f
(x
f
(x )
) f(x
f(x ) (15)
) (15)
или,
по контропозиции f
(x )=f(x
)=f(x )
) x
x =x
=x (16)
(16)
Инъективную
функцию мы будем называть инъекцией.
Термины «всюду определенная инъекция»,
«инъективное отображение» означает
функцию, одновременно всюду определенную
и инъективную. Тождественное отображение
I и любая нигде не определенная функция
является инъекцией.
и любая нигде не определенная функция
является инъекцией.
VII.
Функция f <F,
X,
Y>
тогда и только тогда биективна,
когда она всюду определена, сюръективна
и инъективна. Термины «биективное
соответствие между множествами X
и Y»,
«взаимно – однозначное соответствие
между множествами X
и Y»,
«биективная функция типа X
<F,
X,
Y>
тогда и только тогда биективна,
когда она всюду определена, сюръективна
и инъективна. Термины «биективное
соответствие между множествами X
и Y»,
«взаимно – однозначное соответствие
между множествами X
и Y»,
«биективная функция типа X Y»,
Y»,
«биекция
типа X Y»,
«взаимно – однозначное отображение
множества X
на множество Y»
означает одно и тоже.
Y»,
«взаимно – однозначное отображение
множества X
на множество Y»
означает одно и тоже.
Иногда,
желая сказать, что f
– биекция типа X Y,
говорят «функция f
устанавливает взаимно – однозначное
соответствие между множествами X
и Y».
Y,
говорят «функция f
устанавливает взаимно – однозначное
соответствие между множествами X
и Y».
Тождественное
отображение I множества X
на себя является биекцией.
множества X
на себя является биекцией.
Пусть
f <F,
X,
Y>
- произвольная функция.
<F,
X,
Y>
- произвольная функция.
Инверсия
f =<F
=<F ,
Y,
X>
соответствия f
не обязана быть функцией.
,
Y,
X>
соответствия f
не обязана быть функцией.
Из
ранее доказанного (§ 2, гл. V)
соответствия для произвольного
соответствия Г: Г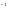 - функция
- функция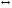 Г – инъективное. Вытекает простое, но
важное утверждение:Критерий
функциональности инверсии:
Инверсия f
Г – инъективное. Вытекает простое, но
важное утверждение:Критерий
функциональности инверсии:
Инверсия f функция f
тогда и только тогда является функцией,
когда функция f
– инъективна.
функция f
тогда и только тогда является функцией,
когда функция f
– инъективна.

Если
f <F,
X,
Y>
- произвольная функция, то для любого
многочлена А:
<F,
X,
Y>
- произвольная функция, то для любого
многочлена А:
f(A)
= {y Y|
(
Y|
( x
x A)[f(x)
= y]} (17)
A)[f(x)
= y]} (17)
f (A)
= {x
(A)
= {x X|
(
X|
( y
y A)[f(x)
= y]} (18)
A)[f(x)
= y]} (18)
Вместо (18) можно написать:
f (A)
=
(A)
=
 {x
{x X|
f(x)
X|
f(x)
 A} (19)
A} (19)
Если
b
 Y,
то элемент a
Y,
то элемент a X
называется прообразом элемента b
относительно функции f,
если f(a)=b.
X
называется прообразом элемента b
относительно функции f,
если f(a)=b.
Из
(19) следует, что f ({b})=
({b})=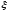 {x
{x X|
f(x)=b} (20)
X|
f(x)=b} (20)
Полный прообраз множества {b} относительно функции f есть множество прообразов элемента b относительно f.
Аналогичное утверждение верно и для произвольного множества.
