Глава VI. Функция.

§1. Функция.

Функция – это функциональное соответствие, т.е. соответствие с функциональным графиком. Если элиминировать ещё один термин «соответствие», можно сказать, что функция- это такая тройка множеств, первая компонента которой является, во-первых, подмножеством прямого произведения второй и третьей компонент и, во-вторых, функциональным графиком.

Итак, тройка множеств <F, X, Y> называется функцией, если

1. FXY

2. В F нет пар с одинаковыми первыми (x=x) и различными вторыми компонентами.

Функции мы будем в дальнейшем обозначать строчными латинскими буквами.

Из определения соответствия, введенного ранее, автоматически вытекает смысл терминов:

«график функции» (первая компонента функции); - Y,

«область отправления функции» - X,

«область прибытия функции» - Y,

«область отправления функции» - прY,

«область значений функции» - прY.

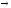Функция с областью отправления X и с областью прибытия Y называется функцией типа XY или по- другому: «Функция f определена в X и принимает свои значения в Y» или в символах: XY, f: XY.

Пусть f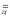<F, X, Y> (1) – произвольная функция.

Если <a, b> F, то элемент b называют значением функции f на а; в этом случае говорят также, что функция f отображает (преобразует) элемент а в элемент b.

Значения функции f на элементы а будем обозначать через f(а) (иногда аf, f).

Если функция f определена на элементу а, т.е. апрF, то существует единственный (в силу функциональности график F) элемент b такой, что <a,b> F. Именно этот элемент b и является, очевидно, значением f(a) функции f на а. Таким образом, выражение f(a) определено для тех и только тех аX, на которых определена функция f, т.е. для апрF.

Или в общем: если f – имя функции <F, X, Y>;

x – переменная с областью значения X.,

то f(x) – форма, определенная для элементов области определения прF и только для них.

Форма f(x) является всюду определенной тогда и только тогда, когда является всюду определенной функция f, т.е. когда прF=X.

Однако, в согласии с нашими общими обозначениями, выражение ! f(x) всегда является всюду определенной высказывательной формой, истинной для элементов множества прF и ложной для элементов множества X прF. Таким образом: ! f(x) x прF (2).

В соответствии с высказанным (§ 2 , гл. IV) условимся высказывательнве формы, содержащие выражения вида f(x) и не содержащие логических законов (), считатьложными при тех значениях переменных, при которых хотя бы одно из выражений вида f(x), входящее в рассмотренную форму, не определено.

Например, если f(a) не определено, f(b) не определено, то форма f(x) _|x=a = f(y)_|y=b определена и ложна.

Согласно оговорке:

[ f(x) =y]f(x) y; f(x)f(y) [f(x)= f(y)] (3)

Например, если ! f(a) л, !f(b) л , тоf(x)f(y)– определение истинна.

С учетом этой оговорки вместо [f(x)а]f(x)a (эта запись не верна) более правильно записывать:

[f(x)а]!f(x)[f(x)a]. (4)

Или по другому: [f(x)а][f(x)а]& [f(x)= а], (5)

но не [f(x)а][f(x)а] &[f(x) а] (6)

Разумеется верно, f(x)а[f(x) а][f(x)= а] (7)

Если аX \ прF, то выражение f(a) не определено, не имеет смысл, ничего не обозначает, ! f(a) – ложное высказывание. Далее имеем:

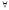(xX)[! f(x)<x, f(x)> F U]. (8)

Если ! f(a), то <a, f(a) >F.

Во многих доказательствах получено следующее тривиальное утверждение:

F(x)=y <x, y>F (9)

где x X, yY.

Наряду с (9) верны так же утверждения (10), (11):

<x, y>F! f(x) & f(x)=y (10)

<x, y>F<x, y>XY & ! f(x)& f(x)=y, (11)

поскольку из f(x) = y следует и ! f(x) и <x, y> XY.

Легко видеть, что если f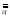<F, X, Y> - произвольная функция, то

F={<x, y>XY | f(x)=y}. (12)

Область определения: прF = {xX | ! f(x)} (13)

Область значения: прF = {yY| (xX)[f(x)=y]}. (14)