
- •Глава V. Соответствие.
- •§1. Соответствие.
- •Операции композиции соответствий
- •§2. Основные свойства соответствия
- •Примеры I-V.
- •Глава VI. Функция.
- •§1. Функция.
- •§2. Основные свойства функции.
- •§3. Теоремы о композициях.
- •Теорема о значении композиции
- •Теорема 2. Теорема о тождественных композициях.
§2. Основные свойства соответствия
Соответствие Г
 <Y,X,Y>
называется функциональным
соответствием или функцией, если его
график Y
функционален, т.е.
<Y,X,Y>
называется функциональным
соответствием или функцией, если его
график Y
функционален, т.е.
 (
( x1)(
x1)( x2)(
x2)( y1)(
y1)( y2)[<
x1,
y1>
y2)[<
x1,
y1> Y
& < x2,
y2>
Y
& < x2,
y2> Y
& x1=
x2&y1
Y
& x1=
x2&y1 y
y ]
(1)
]
(1)
В одной точке (x) только одно значение y

Используя
равносильности для кванторов можем
высказывание (1) преобразовать
( (
( x)U(x)
x)U(x) (
( x)
x)
 U(x)).
U(x)).
(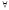 x
x )(
)( x
x )(
)( y
y )(
)( y
y )
) [
[![]() &
&
 ]
] [
[![]()

 (
(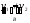 )]
)] (
( x
x )(
)( x
x )(
)( y
y )(
)( y
y )[
)[![]()

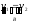 ] (2).
] (2).
Или,
используя, контрапозицию высказывания
(A B=
B= B
B
 A):
A):
( x
x )(
)(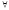 x
x )(
)( y
y )(
)( y
y )[<
x
)[<
x ,
y
,
y >
> Y
& < x
Y
& < x ,
y
,
y >
> Y
& y
Y
& y
 y
y
 x
x
 x
x ](3).
](3).
Высказывания (1)-(3) можно заменить на равносильные, но более простые высказывания:
 (
( x)(
x)( y
y )(
)( y
y )[<x,
y
)[<x,
y >
> Y
& <x, y
Y
& <x, y >
> Y
y
Y
y
 y
y ] (4)
] (4)
( x)(
x)( y
y )(
)( y
y )[<x,
y
)[<x,
y >
> Y&
<x, y
Y&
<x, y >
> Y
Y y
y =
y
=
y ] (5).
] (5).
Соответствие Г
 <Y,
X,
Y>
называется инъективным,
если его график Y
инъективен,
т.е.
<Y,
X,
Y>
называется инъективным,
если его график Y
инъективен,
т.е.
 (
( x
x )(
)( x
x )(
)( y
y )(
)( y
y )[<
x
)[<
x ,
y
,
y >
> Y
& < x
Y
& < x ,
y
,
y >
> Y&
x
Y&
x
 x
x &
y
&
y =
y
=
y ]
(6).
]
(6).

Такого не может быть.
Высказывание (6) равносильно каждому из следующих высказываний (ср. с 1-5):
( x
x )(
)( x
x )(
)( y
y )(
)( y
y )[<
x
)[<
x ,
y
,
y >
> Y
& < x
Y
& < x ,
y
,
y >
> Y
& y
Y
& y =y
=y
 x
x =x
=x ] (7).
] (7).
( x
x )(
)( x
x )(
)( y
y )(
)( y
y )[<
x
)[<
x ,
y
,
y >
> Y
& < x
Y
& < x ,
y
,
y >
> Y
& y
Y
& y
 y
y
 x
x
 x
x ] (8).
] (8).
 (
( x
x )(
)( x
x )(
)( y) [<x
y) [<x ,
y>
,
y> Y
& < x
Y
& < x ,
y>
,
y> Y
& x
Y
& x
 x
x ] (9).
] (9).
( x
x )(
)( x
x )(
)( y)
[<x
y)
[<x ,
y>
,
y> Y
& < x
Y
& < x ,
y>
,
y> Y
Y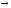 x
x =x
=x ]
(10)
]
(10)
Соответствие Г
 <Y,
M,
M>
называется всюду
определенным,
если его область определения совпадает
с его областью отправления, т.е.
<Y,
M,
M>
называется всюду
определенным,
если его область определения совпадает
с его областью отправления, т.е.
пр Y=
X
(11)
Y=
X
(11)
Легко
видеть, что совпадает Г всюду определено
тогда и только тогда, когда ( x)(
x)(
 y)
[<x,y>
y)
[<x,y> Y]
(12).
Y]
(12).
Соответствие Г
 <Y,
M,
M>
называется сюръективным,
если и его область значения совпадает
с его областью прибытия, т.е. если
<Y,
M,
M>
называется сюръективным,
если и его область значения совпадает
с его областью прибытия, т.е. если
пр Y=Y
(13).
Y=Y
(13).
Соответствие Г сюръективно тогда и только тогда, когда
( y)(
y)(
 x)
[<x,y>
x)
[<x,y> Y]
(14).
Y]
(14).
Соответствие Г
 <Y,
X,
Y>
называется биективным
соответствиям,
или биекцией или взаимно – однозначным
соответствием, если оно функционально,
инъективно, всюду определено и
сюръективно.
<Y,
X,
Y>
называется биективным
соответствиям,
или биекцией или взаимно – однозначным
соответствием, если оно функционально,
инъективно, всюду определено и
сюръективно.
Примеры I-V.
I.
- Функциональное соответствие
II.

- Инъективное соответствие
III.

Соответствие всюду определено (отражение X в Y)
IV.

- Сюръективное соответствие
(отображение X наY)
V.

- Биективное соответствие
Если среди соответствий между множествами X и Y существует взаимно – однозначные соответствия, то говорят, что между множествами X и Y можно установить взаимно – однозначные соответствия.
Для
того чтобы доказать, что заданными между
множествами X,
Y
можно установить взаимно – однозначные
соответствия, нужно задать (или доказать,
что существует) такой график Y X
X Y,
чтобы тройка <Y,
X,
Y>
был биекцией.
Y,
чтобы тройка <Y,
X,
Y>
был биекцией.
Если
мы каждому элементу множества X
поставим в соответствие один элемент
множества Y,
то получим некоторый график Y X
X Y,
причем соответствие <Y,
X,
Y>
будет уже всюду определенным («каждому»)
и функциональным («один»).
Y,
причем соответствие <Y,
X,
Y>
будет уже всюду определенным («каждому»)
и функциональным («один»).
Если нам удастся затем доказать, что в построенном нами соответствии разный элемент множества Y и каждый элемент множества Y соответствует хотя бы одному элементу множества X, будет доказано, что наше соответствие вдобавок инъективно («разный … разные») и сюръективно («каждый») и, следовательно, биективно.
При доказательстве биективности построенного соответствия («каждому элементу множества X ставиться в соответствии один элемент множества Y») два из четырех свойств: всюду определенность и функциональность можно уже не проверять. Они обеспечиваются автоматичеки, сами построением, а дается нам извне, в готовом виде, то проверять надо все четыре свойства.
Введенные выше 5 свойств (I-V) мы будем называть основными свойствами соответствий.
Из доказанного в § 5 гл. III следует, что для любого соответствия Г:
Г - инъективное
- инъективное Г – функция, (15)
Г – функция, (15)
Г - функция
- функция Г – инъективно. (16)
Г – инъективно. (16)
Очевидно также (см. §1), что
Г - сюръективное
- сюръективное Г – всюду определенное, (17)
Г – всюду определенное, (17)
Г - всюду определенное
- всюду определенное Г– сюръективное. (18)
Г– сюръективное. (18)
Из (15) – (18) следует, что
Г - биекция
- биекция Г- биекция.
Г- биекция.
Таким образом, если между множествами X и Y можно установить взаимно – однозначное соответствие, то между множествами Y и X тоже можно установить взаимно – однозначное соответствие.
Из доказанного в § 5 гл. III следует, что композиция функций есть функция и композиция инъективных соответствий инъективна.
Аналогичные утверждения для произвольных всюду определенных, сюръективных и биективных соответствий не верны.
Например,
если не пустые множества Y
и Z
не пересекаются (Y 0,
Z
0,
Z 0,
Y
0,
Y Z=0)
и Г
Z=0)
и Г <Y
<Y ,
Y,
Y>,
,
Y,
Y>,
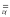 <Z
<Z ,
Z,
Z>,
то Г и
,
Z,
Z>,
то Г и
 всюду определны и не сюръективны, а Г
всюду определны и не сюръективны, а Г
 =
<0,Y,
Z>
не всюду определено и не сюръективно.
=
<0,Y,
Z>
не всюду определено и не сюръективно.
Если,
однако область прибытия соответствия
Г совпадает с областью отправления
соответствия 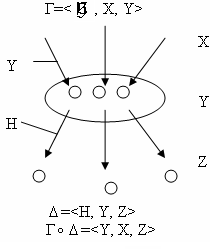
 (важнейший
для практики случай) и соответствия Г,
(важнейший
для практики случай) и соответствия Г,
 всюду определно, но и их композиция Г
всюду определно, но и их композиция Г
 всюду определена.
всюду определена.
Аналогичное утверждение верно (при указанном выше достаточном условии) также для сюръективных и, следовательно, биективных соответствий.
Таким образом, если между множеством X и Y можно установить взаимно – однозначное соответствие и между множествами Y и Z можно установить взаимно – однозначное соответствие, то между множествами X и Z тоже можно установить взаимно – однозначное соответствие.
Между
множествами X
и X,
очевидно, всегда можно установить
взаимно – однозначное соответствие.
Примером такого соответствия является
биекция <
 ,X,
X>,
в которой каждому элементу a
,X,
X>,
в которой каждому элементу a X
соответствует а и только а.
X
соответствует а и только а.
Если
X
и Y
- конечные множества ( =m,
=m,
 =n),
то между множествами X
и Y
тогда и только тогда можно установить
взаимно - однозначное соответствие,
когда m=n
, причем при этом условии различных
взаимно – однозначных соответствий
между X
и Y
существует P
=n),
то между множествами X
и Y
тогда и только тогда можно установить
взаимно - однозначное соответствие,
когда m=n
, причем при этом условии различных
взаимно – однозначных соответствий
между X
и Y
существует P =n!
.
=n!
.
Примеры взаимно – однозначных соответствий

