
- •Глава V. Соответствие.
- •§1. Соответствие.
- •Операции композиции соответствий
- •§2. Основные свойства соответствия
- •Примеры I-V.
- •Глава VI. Функция.
- •§1. Функция.
- •§2. Основные свойства функции.
- •§3. Теоремы о композициях.
- •Теорема о значении композиции
- •Теорема 2. Теорема о тождественных композициях.
Утверждения (9),(10) являются аналогами законов де Моргана.
Докажем
(9). Фиксируем
произвольную форму U(x).
Пусть высказывание
 (
( x)
U(x)
истинно. Тогда по определению отрицания
(
x)
U(x)
истинно. Тогда по определению отрицания
( x)
U(x)
– ложно.
x)
U(x)
– ложно.
Следовательно, не для любого значения переменной x высказывание U(x) истинно. Значит, существует такое значение переменной x, для которого U(x) ложно. Обозначим одно из таких значений через а.
Итак
а М
иU(а)
– ложно. Следовательно,
М
иU(а)
– ложно. Следовательно,
 U(а)
– истинно. Значит, существует такое x,
что
U(а)
– истинно. Значит, существует такое x,
что
 U(x)
истинно, т.е. (
U(x)
истинно, т.е. ( x)
x)
 U(x)
истинно.
U(x)
истинно.
Пусть
теперь, с другой стороны, высказывание
( x)
x)
 U(x)
– истинно. Тога, по определению квантора
существования, существует такое значение
переменной x,
что
U(x)
– истинно. Тога, по определению квантора
существования, существует такое значение
переменной x,
что
 U(x)
– истинно. Обозначим одно из таких
значений через а.
U(x)
– истинно. Обозначим одно из таких
значений через а.
Итак,
а М
и
М
и U(x)
истинно. Следовательно, U(а)
ложно. Но тогда, по определению квантора
общности, ложно и (
U(x)
истинно. Следовательно, U(а)
ложно. Но тогда, по определению квантора
общности, ложно и ( x)
U(x),
а значит,
x)
U(x),
а значит,
 (
( x)
U(x)
истинно.
x)
U(x)
истинно.
Доказательство (10).
Пусть
 (
( x)
U(x)-
истинно. Тогда (
x)
U(x)-
истинно. Тогда ( x)
U(x)-
ложно. Обозначим это значение x
через а. Имеем, а
x)
U(x)-
ложно. Обозначим это значение x
через а. Имеем, а М
иU(а)
– ложно. Следовательно,
М
иU(а)
– ложно. Следовательно,
 U(а)
– истинно, а значит и истинно (
U(а)
– истинно, а значит и истинно ( x)
x)
 U(x).
U(x).
Пусть
теперь истинно ( x)
x)
 U(x).
Следовательно, U(x)-
ложно. Значит,
U(x).
Следовательно, U(x)-
ложно. Значит,
 (
( x)
U(x)
– истинно.
x)
U(x)
– истинно.
Прежде чем переходить к общему случаю, рассмотрим ещё один простой случай.
2)
Пусть U(x,у)
– двухместная высказывательная форма,
где x М
, у
М
, у Z.
Z.
Тогда имеем место:
Зависят:
от
y
- ( x
x М)
U(x,у), (
М)
U(x,у), ( x)
U(x,у)
(11)
x)
U(x,у)
(11)
x
- ( y
y Z)
U(x,у), (
Z)
U(x,у), ( y
) U(x,у) (12)
y
) U(x,у) (12)
y
- ( x
x M)
U(x,у), (
M)
U(x,у), ( x
) U(x,у) (13)
x
) U(x,у) (13)
x
- ( y
y Z)
U(x,у), (
Z)
U(x,у), ( y
) U(x,у) (14)
y
) U(x,у) (14)
(11)-(14) – являются одноместными высказывательными формами зависящие соответственно, от y, x, y, x.
Поскольку (11)-(14) – являются одноместными высказывательными формами, то на каждую из них можно навесить каждый из двух кванторов. При этом получается восемь высказываний. Без указаний областей значений переменной эти высказывания имеют вид:
( x)
(
x)
( y
) U(x,у) (15)
y
) U(x,у) (15)
( y
) (
y
) (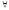 x)
U(x,у) (16)
x)
U(x,у) (16)
( x
) (
x
) ( y
) U(x,у) (17)
y
) U(x,у) (17)
( y
) (
y
) ( x
) U(x,у) (18)
x
) U(x,у) (18)
( x)
(
x)
( y
) U(x,у) (19)
y
) U(x,у) (19)
( y
) (
y
) ( x)
U(x,у) (20)
x)
U(x,у) (20)
(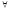 y
) (
y
) ( x
) U(x,у) (21)
x
) U(x,у) (21)
( x
) (
x
) ( y
) U(x,у) (22)
y
) U(x,у) (22)
Пример
2. пусть область значений переменных х
и у – множество М
 .
.
Образуем одноместные высказывательные формы:
Истина
при у=0 ( x)
x)
 (
( y
)
y
)
 -
ложная
-
ложная
истина- ( x
)
x
)
 (
( y
)
y
)
 -
истина
-
истина
Из них:
1.
Истина. Форма ( x)
x)
 при у=0, т.к. для любого а
при у=0, т.к. для любого а М
имеем а
М
имеем а 0.
Форма (
0.
Форма ( x)
x)
 при любом у
при любом у 0
ложна, т.к. если у = а
0
ложна, т.к. если у = а М
и а
М
и а 0,то
0,то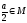 и
и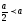 .
.
2.
Форма (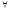 y
)
y
)
 ложна при любом значении х, т.к. если бы
она истинной при х = а
ложна при любом значении х, т.к. если бы
она истинной при х = а М,
это означало бы, что а- наибольшее
действительное число.
М,
это означало бы, что а- наибольшее
действительное число.
3.
Форма ( x
)
x
)
 истинна при любом у, хотя бы в силу того,
что для а
истинна при любом у, хотя бы в силу того,
что для а М
имеем а
М
имеем а а.
а.
4.
Форма ( y
)
y
)
 истина при всех х.
истина при всех х.
5.
Форма (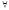 y
) (
y
) ( x)
x)
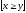 ложна, т.к. при всех у истинна форма (
ложна, т.к. при всех у истинна форма ( x)
x)

6.
Аналогично (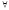 x)
(
x)
( y
)
y
)
 -
ложно.
-
ложно.
7.
Формы ( x
) (
x
) ( y
)
y
)
 -
истина.
-
истина.
( y
) (
y
) ( x
)
x
)
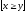 -
истина.
-
истина.
8.
Форма ( y
) (
y
) ( x)
x)
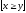 -
истинна.
-
истинна.
9.
Форма ( x)
(
x)
( y
)
y
)
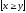 -
истинна.
-
истинна.
10.
Форма (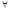 y
) (
y
) ( x
)
x
)
 -
истинна.
-
истинна.
11.
Форма ( x
) (
x
) ( y
)
y
)
 -
ложна.
-
ложна.
Правила, аналогичные правилам (9),(10), верны так же для формы (11)-(14) и высказываний (15)-(22).
Например:
 (
( x)
U(x,у)
x)
U(x,у) (
( x
)
x
)
 U(x,у) (23)
U(x,у) (23)
 (
( y
) U(x,у)
y
) U(x,у)
 (
( y
)
y
)
 U(x,у) (24)
U(x,у) (24)
 (
( x
) (
x
) ( y
) U(x,у)
y
) U(x,у)
 (
( х)
(
х)
( y
)
y
)
 U(x,у) (25)
U(x,у) (25)
 (
( y
) (
y
) ( x
) U(x,у)
x
) U(x,у)
 (
( y
) (
y
) (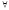 х)
х) U(x,у) (26)
U(x,у) (26)
Словами правило, выраженное равносильностями (9),(10),(23)-(26) и всеми аналогичными ими равносильностями, можно сформулировать так:
Чтобы найти отрицание выражения, начинающегося с кванторов, надо каждый квантор заменить на двойственный (т.е. квантор общности на квантор существования и наоборот) и перенести знак отрицания за кванторы.
Докажем равносильность (23)
Фиксируем
форму U
и возьмем произвольное значение
переменной у, скажем, b
 .
.
Нам
надо доказать, что
 (
( x)
U(x,b)
x)
U(x,b)
 (
( x
)
x
)
 U(x,b) (27).
U(x,b) (27).
Рассмотрим
выражение
 (
(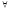 x)
U(x,b).
Оно представляет собой отрицание
результата навешивания квантора
общности на одноместную форму U(x,b).
x)
U(x,b).
Оно представляет собой отрицание
результата навешивания квантора
общности на одноместную форму U(x,b).
Следовательно, (27) вытекает из (9). Но (27), вследствие произвольности выбора значения переменной у, означает (23).
Докажем
равносильность (25). Рассмотрим выражение
 (
( x
)(
x
)( y
) U(x,у).
Оно представляет собой отрицание
результата навешивания квантора
существования на одноместную форму
(12).
y
) U(x,у).
Оно представляет собой отрицание
результата навешивания квантора
существования на одноместную форму
(12).
Следовательно в силу (10)
 (
( x
) (
x
) ( y
) U(x,у)
y
) U(x,у)
 (
( x)
x)
 (
( y
) U(x,у) (28).
y
) U(x,у) (28).
В
силу (23)
 (
( y
) U(x,у)
y
) U(x,у)
 (
( y
)
y
)
 U(x,у) (29).
U(x,у) (29).
Заменяя в (28) левую часть равносильности (29) на правую, получим (25).
Между
высказываниями (15)-(22) имеются некоторые
связи. Легко видеть, что: (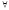 x)
(
x)
( y
) U(x,у)
y
) U(x,у)
 (
(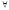 y
) (
y
) (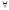 x)
U(x,у) (30)
x)
U(x,у) (30)
( x
) (
x
) ( у
)U(x,у)
у
)U(x,у)
 (
( у
) (
у
) ( x
) U(x,у) (31).
x
) U(x,у) (31).
Из (30), (31) следует: одноименные кванторы можно представлять.
«Разноименные» кванторы можно представить только «в одну сторону».
Если
( x
) (
x
) ( y
) U(x,у)
y
) U(x,у)
 U,
то (
U,
то ( y
) (
y
) ( x
) U(x,у)
x
) U(x,у)
 U (32).
U (32).
Если
( x
) (
x
) ( x)
U(x,у)
x)
U(x,у)
 U,
то (
U,
то ( x)
(
x)
(
 у
)U(x,у)
у
)U(x,у)
 U (33).
U (33).
Утверждение обратное (32), (33):
если
( y
) (
y
) ( x
) U(x,у)
x
) U(x,у)
 U,
то (
U,
то ( x
) (
x
) ( y
) U(x,у)
y
) U(x,у)
 U (34)
не верно. Например, (
U (34)
не верно. Например, ( y
) (
y
) ( x
)
x
)

 U,
однако (
U,
однако ( x
) (
x
) ( y
)
y
)

 U.
U.
3)
Пусть
U(x ,
…, x
,
…, x )
– s-
местная высказывательная форма (s
)
– s-
местная высказывательная форма (s );
);
x
x
…….
x .
.
В
силу введенных выше обозначений для
любого i,

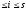 выражения
выражения
(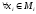 )U(x
)U(x ,
…, x
,
…, x ),
(
),
(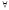 x
x )U(x
)U(x ,
…, x
,
…, x ) (35)
) (35)
( x
x
 M
M )U(x
)U(x ,
…, x
,
…, x ),
(
),
( x
x )U(x
)U(x ,
…, x
,
…, x ) (36)
) (36)
Являются (s-1) – местными высказывательными формами зависящими от (свободных) переменных x1, …, xi-1 , xi+1, …, xs. Буква в выражениях (35), (36) является связанной переменной. Навешивание квантора по переменной xi.
По
определению квантора общности высказывание
(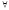 x
x )
U(a1,
a2,
… , a
i-1,
x
i,
a
i+1,
… , as)
(37) истинно тогда и только тогда, когда
для любого значения a
)
U(a1,
a2,
… , a
i-1,
x
i,
a
i+1,
… , as)
(37) истинно тогда и только тогда, когда
для любого значения a
 M
M переменной x
переменной x высказывание U(a1,
a2,
… , a
i-1,
xi,
ai+1,
… , as)
(38) истинно.
высказывание U(a1,
a2,
… , a
i-1,
xi,
ai+1,
… , as)
(38) истинно.
По
определению квантора существования
высказывание ( xi)
U(a1,
…, x
i,
ai+1,
…, as)
(39) истинно тогда и только тогда, когда
существует такое значение ai
xi)
U(a1,
…, x
i,
ai+1,
…, as)
(39) истинно тогда и только тогда, когда
существует такое значение ai Mi
переменной x
Mi
переменной x ,
для которого высказывание (38) истинно.
,
для которого высказывание (38) истинно.
Навешивая
на каждую из (s-1)
- местных высказывательных форм (35), (36)
любой из кванторов по любой из свободных
переменных, мы получим (при s 2)
(s-2)
– местные высказывательные формы или
при (s=2)
высказывания, и т.д. после того как
навешано уже s
кванторов, получаются высказывания.
2)
(s-2)
– местные высказывательные формы или
при (s=2)
высказывания, и т.д. после того как
навешано уже s
кванторов, получаются высказывания.
Отличные закономерности остаются верными и в общем случае:
Отрицание выражения, начинающегося с кванторов, получается заменой каждого квантора на двойственной и переменными знака отрицания за кванторы:
 (
( x
i)
U(x1,
…, xs)
x
i)
U(x1,
…, xs)
 (
( x
i)
x
i)
 U(x1,
…, x
s) (40)
U(x1,
…, x
s) (40)
 (
( x
i)
U(x1,
…, xs)
x
i)
U(x1,
…, xs)
 (
( x
i)
x
i) U(x
1,
…, x
s) (41)
U(x
1,
…, x
s) (41)
II. Одноименные кванторы можно переставить
( x
i)
(
x
i)
( x
j)
U(x
1,
…, x
s)
x
j)
U(x
1,
…, x
s)
 (
( x
j)(
x
j)( x
i)
U(x
1,
…, x
s) (42)
x
i)
U(x
1,
…, x
s) (42)
( x
i)
(
x
i)
( x
j)
U(x
1,
…, x
s)
x
j)
U(x
1,
…, x
s)
 (
( x
j)(
x
j)( x
i)
U(x
1,
…, x
s)
(43)
x
i)
U(x
1,
…, x
s)
(43)
III. Разноименные кванторы можно переставлять только в одну сторону:
если
( x
i)
(
x
i)
( x
j)
U(x
1,
…, x
s)
x
j)
U(x
1,
…, x
s)
 U,
U,
то
( x
j)(
x
j)( x
i)
U(x
1,
…, x
s)
x
i)
U(x
1,
…, x
s)
 U.
(44)
U.
(44)
Обратное вообще говоря не верно.
Заметим, что (44) можно выразить еще так:
( x
i)(
x
i)(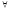 x
j)
U(x
1,
…, x
s)
x
j)
U(x
1,
…, x
s) (
( x
j)(
x
j)( x
i)
U(x
1,
…, x
s)
x
i)
U(x
1,
…, x
s)
 U
(45)
U
(45)
Полезны таблицы «аналогий»:
№1 №2
|
& |
| |||
|
|
| |||
|
& |
|
|
| |
|
|
|
\ |
пр | |
Пусть
U(x)
– одноместная высказывательная форма,
x
 M,
A
M,
A M.
Образуем выражение (
M.
Образуем выражение ( x
x A)
U(x)
(46)
A)
U(x)
(46)
( x
x A)
U(x)
(47).
A)
U(x)
(47).
Кванторы
( x
x A),
(
A),
( x
x A)
– ограниченные кванторы.
A)
– ограниченные кванторы.
Ограниченные кванторы связаны с обычными, так сказать, «неограниченными» кванторами:
( x
x A)U(x)
A)U(x)
 (
( x
x M)
[x
M)
[x A
A U(x)] (48)
U(x)] (48)
( x
x A)U(x)
A)U(x)
 (
( x
x M) [x
M) [x A&U(x)] (49).
A&U(x)] (49).
Указанные свойства (I-III) операции навешивания «неограниченных» кванторов сохраняются и для ограниченных кванторов. Например,
 (
(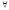 x
x A)
(
A)
( y
y B)U(x,y,z)
B)U(x,y,z)
 (
( x
x A) (
A) ( y
y B)
B) U(x,y,z).
U(x,y,z).
Глава V. Соответствие.
§1. Соответствие.
Слово «соответствие» уже встречалось нам в словосочетании « взаимно – однозначное соответствие ».
Говорят,
что между множествами X
и Y
установлено взаимно – однозначное
соответствие, если указано такое
подмножество Y
 X
X
 Y,
которые обладают некоторыми свойствами,
т.е. выделен график Y
Y,
которые обладают некоторыми свойствами,
т.е. выделен график Y
 X
X Y
с определенными свойствами.
Y
с определенными свойствами.
Следовательно,
взаимно – однозначные соответствие
между множествами X
и Y
полностью характеризуется, во0первых,
смежными множествами X
и Y,
во-вторых, графиком Y X
X Y
.
Y
.
Что же такое само взаимно – однозначное соответствие? Что такое соответствие вообще?
Соответствие- это тройка множеств, первая компоненты которой являются подмножеством прямого произведения второй и третьей компонент.
Еще раз по другому:
Тройка
множеств < Y,
X,
Y>
называется соответствием, если Y
 X
X Y.
Y.
Соответствие мы будем обозначать в основном прописными греческими буквами.
Пусть
Г <Y,X,Y>
- произвольное соответствие. (1)
<Y,X,Y>
- произвольное соответствие. (1)
пр Y
Y X
X
пр Y
Y
 Y
Y
<a,b> Y
Y
Из определения соответствия следует, что его первая компонента Y есть график.
График Y, т.е. первая компонента соответствия Г, называется графиком соответствия.
Множество X, т.е. вторая компонента соответствия Г, называется областью отправления соответствия.
Множество Y, т.е. третья компонента соответствия Г, называется областью прибытия соответствия.
Соответствие Г с областью отправления X и областью прибытия Y называется соответствием между множествами X и Y.
Из трех основных множеств: графики, области отправления и области прибытия, еще два важных множества неразрывно связаны с каждым соответствием.
Область
определения
графика Y
соответственно Г, т.е. множество пр Y
называется областью
определения соответствия.
Y
называется областью
определения соответствия.
Область
значения графика Y
соответствия Г, т.е. множество пр Y
называется областью
значений соответствия.
Y
называется областью
значений соответствия.
Если
<a,b> пр
пр Y,
то мы будем говорить, что соответствие
Г определено
на элементе а.
Y,
то мы будем говорить, что соответствие
Г определено
на элементе а.
Два соответствия равны тогда и только тогда, когда равны их графики, области определения и области прибытия.
Примеры:
1) Г <{
<a,
<{
<a, >,
<a,
>,
<a, >
, <b,
>
, <b, >},
{a,b,c},
{
>},
{a,b,c},
{ ,
, ,
, }
>
}
>
X Y=
{<a,
Y=
{<a, >,
<a,
>,
<a, >,
<a,
>,
<a, >,
<b,
>,
<b, >,
<b,
>,
<b, >,
<b,
>,
<b, >,
<c,
>,
<c, >,
<c,
>,
<c,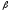 >,
<c,
>,
<c, >}.
>}.
Y
 X
X Y={<a,
Y={<a, >,
<a,
>,
<a, >
, <b,
>
, <b, >}.
>}.
Изобразим соответствие Г графически:
В
соответствии Г элемент 
 соответствует
элементам а и b
и элемент
соответствует
элементам а и b
и элемент
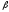 элементу а, но сказать, что в соответствии
Г элемент а соответствует элементу
элементу а, но сказать, что в соответствии
Г элемент а соответствует элементу ,
не верно.
,
не верно.
Областью
определения
соответствия Г является множество {a,
b},
областью
значений –
множество { ,
, }.
}.
Соответствие Г определено на a и на b и не определено на с.
Очевидно,
что если Y X
X Y,
то Y
Y,
то Y
 X
X Y.
Следовательно, если тройка <Y,X,Y>
является соответствием, то тройка < Y
Y.
Следовательно, если тройка <Y,X,Y>
является соответствием, то тройка < Y
 ,
Y,
X>
тоже является соответствием.
,
Y,
X>
тоже является соответствием.
Тройку
< Y ,
Y,
X>
принято называть инверсией соответствия
Г и обозначать Г
,
Y,
X>
принято называть инверсией соответствия
Г и обозначать Г .
Г
.
Г
 <Y
<Y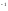 ,
Y,
X>,
Г
,
Y,
X>,
Г <Y,
X,Y>
очевидно, область определения пр
<Y,
X,Y>
очевидно, область определения пр Y
Y инверсии соответствия Г равна области
значений пр
инверсии соответствия Г равна области
значений пр Y
самого соответствия Г, а область значения
инверсии соответствия Г равна области
определения соответствия Г.
Y
самого соответствия Г, а область значения
инверсии соответствия Г равна области
определения соответствия Г.
Далее,
очевидно (Г )
) =Г
(2).
=Г
(2).
Операции композиции соответствий
Если
Г <Y,X,Y>,
<Y,X,Y>,
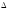
 <M,Z,U>,
то композицией соответствий Г и
<M,Z,U>,
то композицией соответствий Г и
 являются:
являются:
 <Y
<Y М,
Х, U>
т.е. соответствие
М,
Х, U>
т.е. соответствие
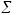 называетсякомпозицией
соответствий
Г
и
называетсякомпозицией
соответствий
Г
и
 ,
если график соответствия
,
если график соответствия является композицией (Y
является композицией (Y М)
графиков соответствий Г и
М)
графиков соответствий Г и
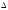 ,
область определения соответствия
,
область определения соответствия равна области отправления соответствия
Г, а область значений соответствия
равна области отправления соответствия
Г, а область значений соответствия равна области значений соответствия
равна области значений соответствия .
.
Очевидно:
(Г

 )
)
 =Г
=Г (
(

 )
(3)
)
(3)
Возьмем
n
произвольных соответствий (n 3)
Г1,
Г2,
…, Гn
и в выражении Г1
3)
Г1,
Г2,
…, Гn
и в выражении Г1 Г2
Г2
 …
… Гn
фиксируем произвольную расстановку
скобок, приводящую последовательному
полезному компонированию соответствий.
Гn
фиксируем произвольную расстановку
скобок, приводящую последовательному
полезному компонированию соответствий.
Графиком
полученного в результате соответствия
 является композиция графиков соответствий
Г1,
Г2,
…, Гn,
область отправления соответствия
является композиция графиков соответствий
Г1,
Г2,
…, Гn,
область отправления соответствия
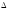 равна области соответствия Г1
и область прибытия соответствия
равна области соответствия Г1
и область прибытия соответствия
 составляет с областью прибытия
соответствия Гn.
составляет с областью прибытия
соответствия Гn.
Таким
образом, как и для графиков, можно
определить композицию Г1 Г2
Г2 …
… Гn
произвольного (конечного) компонирования
соответствия Г1,Г2,…,
Гn
при любой расстановке скобок.
Гn
произвольного (конечного) компонирования
соответствия Г1,Г2,…,
Гn
при любой расстановке скобок.
Далее
очевидно, что (Г

 )
) =
=

 Г
Г (4)
(4)
Или
далее общее: (Г1 Г2
Г2
 …
… Гn)
Гn) =
Г
=
Г
 Г
Г
 …
… Г
Г
 Г
Г (5)
(5)
Введем два новых понятия: образ и прообраз.
Пусть Г
 <Y,X,Y>
- произвольное соответствие, А-произвольное
множество.
<Y,X,Y>
- произвольное соответствие, А-произвольное
множество.
Образом множества А относительно соответствия Г называется и через Г(А) обозначается множество тех элементов из области прибытия Y соответствия Г какому-нибудь элементу множества А.
Таким
образом Г(А)
 {y
{y Y|
(
Y|
( x
x A)
[<x,y>
A)
[<x,y> Y]}
(6) Y-
область прибытия.
Y]}
(6) Y-
область прибытия.
В
частности, Г({f})={
y Y|
(
Y|
( x
x {f})
[<x,y>
{f})
[<x,y> Y]}
(7) что, конечно, можно записать проще
Г({a})={y
Y]}
(7) что, конечно, можно записать проще
Г({a})={y Y|
<a,y>
Y|
<a,y> Y},
(8) т.е. Г({a})
– это множество элементов, соответствующих
элементу а в соответствии Г (множество
концов стрелок, выходящих из а).
Y},
(8) т.е. Г({a})
– это множество элементов, соответствующих
элементу а в соответствии Г (множество
концов стрелок, выходящих из а).
Легко
видеть, что Г(А)=
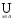 Г({x})
(9).
Г({x})
(9).
Графически
Г(А)- это множество концов стрелок,
выходящих из элементов множества А.
Каждое из следующих утверждений очевидно (и легко доказывается):
A B
B Г(А)
Г(А)
 Г(B) (10)
Г(B) (10)
Г(А)=Г(А пр
пр Y) (11)
Y) (11)
Г(А)=0
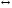 А
А пр
пр Y=0 (12)
Y=0 (12)
Г(А)
 пр
пр Y (13)
Y (13)
Г(пр Y)=
пр
Y)=
пр Y (14)
Y (14)
пр Y
Y A
A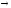 Г(А) = пр
Г(А) = пр Y (15)
Y (15)
Г(0) = 0 (16)
Пример
1). Если
М {a,b,c,d,e,g},
график Y
{a,b,c,d,e,g},
график Y {<a,e>,
<c,b>,
<d,d>,
<e,c>,
<g,b>,
<a,d>},
Г
{<a,e>,
<c,b>,
<d,d>,
<e,c>,
<g,b>,
<a,d>},
Г <Y,
M,
M>,
A
<Y,
M,
M>,
A {a,
b,
d,
g},
B={a,
b,
c,
d,
g},
тогда Г(А)= {e,d,b}.
{a,
b,
d,
g},
B={a,
b,
c,
d,
g},
тогда Г(А)= {e,d,b}.
Для
(10) A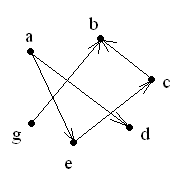
 B={a,
b,
d,
g}
B={a,
b,
d,
g} {a,
b,
c,
d,
g}
{a,
b,
c,
d,
g} Г(А)
Г(А) Г(В).
Г(В).
Г(В)= {d, e, b, d, b} = {e, d, b}.
Для
(11) Г(А)= Г({a,
b,
d,
g} {a,
c,
d,
e,
g})
= Г({a,d,g})=
{e,
d,
b}.
{a,
c,
d,
e,
g})
= Г({a,d,g})=
{e,
d,
b}.
Для
(13) Г(А)
 пр
пр Y=
{e,
b,
d,
e}.
Y=
{e,
b,
d,
e}.
Для
(14) Г(пр Y)=
пр
Y)=
пр Y
Y Г({a,
c,
d,
e,
g})
= {b,
d,
c,
e}.
Г({a,
c,
d,
e,
g})
= {b,
d,
c,
e}.
Для
(15) D=
{a,
c,
b,
d,
e,
g} пр
пр Y
= {a,
c,
d,
e,
g}
Y
= {a,
c,
d,
e,
g} Г(D)
= {d,
e,
b,
d,
c,
b}
= {d,
e,
b,
c}
= пр
Г(D)
= {d,
e,
b,
d,
c,
b}
= {d,
e,
b,
c}
= пр Y.
Y.
Пример
2).
Если Y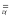
 {<x,
y>
{<x,
y> D
D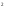 |
y-3x+2=0},
|
y-3x+2=0},
Г <Y,
D, D>,
<Y,
D, D>,
A [2, 3),
[2, 3),
Г(А)= [4, 7).

Данный
пример подсказывает нам гипотезу, что
для любого соответствия Г <Y,
X,
Y>
и множества А
<Y,
X,
Y>
и множества А
Г(А)=
пр [(A
[(A Y)
Y) Y] (17)
Y] (17)
Это равенство выражает образ Г(А) множество А при соответствии Г через график соответствия Г.
Именно этим правилом удобно пользоваться при нахождении Г(А).
Если
Г,
 - произвольные соответствия и А-
произвольное множество, то
- произвольные соответствия и А-
произвольное множество, то
(Г
 )
(А) =
)
(А) = (Г(А)) (18).
(Г(А)) (18).
Равенство
(18) вскрывает самую суть понятия
«композиция соответствий». Оно показывает,
что «применить» к множеству А композицию
соответствий Г и
 - это значит последовательно (сначала
Г, потом
- это значит последовательно (сначала
Г, потом )
применить эти соответствия. Следовательно
– это последовательное «применение»
соответствий.
)
применить эти соответствия. Следовательно
– это последовательное «применение»
соответствий.
Пример
3).
Г <{
<{ },
{
},
{
 },
{
},
{ }>.
}>.

 <{
<{ },
{
},
{ },
{
},
{ }>.
}>.
A {a,b}.
{a,b}.
Г
 = <Y
= <Y H,
X,
U>=
<{<a,
2>, <c,
2>, <c,
3>}, {a,
b,
c,
d},
{1, 2, 3, 4}>.
H,
X,
U>=
<{<a,
2>, <c,
2>, <c,
3>}, {a,
b,
c,
d},
{1, 2, 3, 4}>.
Г(А)=пр [A
[A Y
Y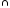 Y]=пр
Y]=пр [{
[{ }
} {
{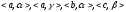 }]
= пр
}]
= пр [
[ ]
= {
]
= { }.
}.
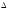 (Г(А))
= (Г
(Г(А))
= (Г
 )(А)
= пр
)(А)
= пр [Г(А)
[Г(А) U
U H]
= пр
H]
= пр [{
[{ }
} {1, 2, 3, 4}
{1, 2, 3, 4} H]
= пр
H]
= пр [{
[{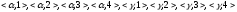 }
} {
{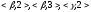 }]
= пр
}]
= пр [<
[< >]
= {2}.
>]
= {2}.
Пример
4). Если
Г- соответствие между D
и D
с графиком Y
 {<x,
y>
{<x,
y> D
D |
y=sinx},
а
|
y=sinx},
а
 -
соответствие междуD
и D
с графиком H
-
соответствие междуD
и D
с графиком H
 {<x,
y>
{<x,
y> D
D |
y=lgx},
то композиция Г
|
y=lgx},
то композиция Г
 будет иметь графиком множество
будет иметь графиком множество {<x,
y>
{<x,
y> D
D |
y=lgsinx}.
|
y=lgsinx}.
Утверждение
(18) можно обобщить на любое число
соответствия. Если Г ,
Г
,
Г ,
… , Г
,
… , Г - произвольные соответствия (n
- произвольные соответствия (n 3)
и А – произвольное множество, то (Г
3)
и А – произвольное множество, то (Г
 Г
Г
 …
… Г
Г )
(А) = Г
)
(А) = Г (…(
Г
(…(
Г (
Г
(
Г (А)))
…) (19).
(А)))
…) (19).
2)
Пусть
Г <Y,X,Y>
- произвольное соответствие, А –
произвольное множество.
<Y,X,Y>
- произвольное соответствие, А –
произвольное множество.
Полным
прообразом
множества А относительно соответствия
Г называется и через Г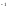 (А)
обозначается множество тех элементов
области отправления соответствия Г,
каждому из которых соответствует в
соответствии Г какой-нибудь элемент
множества А, таким образом: Г
(А)
обозначается множество тех элементов
области отправления соответствия Г,
каждому из которых соответствует в
соответствии Г какой-нибудь элемент
множества А, таким образом: Г (А)
(А) {x
{x X|
(
X|
( y
y A)
[<x,y>
A)
[<x,y> Y]}
(20)
Y]}
(20)
Для
нахождения Г (А)
удобно пользоваться формулой (21)
(А)
удобно пользоваться формулой (21)
Г (А)=
пр
(А)=
пр [(X
[(X А)
А) Y] (21)
Y] (21)
(
ср. Г(А)= пр [А
[А Y
Y Y]
).
Y]
).
Если
Г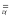 <Y,X,Y>,
то Г
<Y,X,Y>,
то Г =
<Y
=
<Y ,
Y,
X>.
,
Y,
X>.
По
определению образа, образ множества А
при соответствии Г равен:
равен:
Г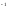 (А)={x
(А)={x X|
(
X|
( y
y A)
[<y,x>
A)
[<y,x> Y
Y ]
} (22).
]
} (22).
Следовательно,
полный прообраз множества А при
соответствии Г совпадает с образом
множества А при соответствии Г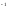 (ср.(22), (20)).
(ср.(22), (20)).
Это позволяет любое утверждение, относящееся к полному прообразу, свести к некоторому утверждению об образе и наоборот.
Таким образом, получаем, в частности, аналоги утверждений (8-19):
(8)
Г ({a})
= { x
({a})
= { x X|
<x,
a>
X|
<x,
a> Y
} (23)
Y
} (23)
(9)
Г (A)
=
(A)
=
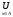 Г
Г ({x}) (24)
({x}) (24)
(10)
А В
В Г
Г (A)
(A)
 Г
Г (В) (25)
(В) (25)
(11)
Г (A)
= Г
(A)
= Г (A
(A
 пр
пр Y) (26)
Y) (26)
(12)
Г (A)
=0
(A)
=0 A
A пр
пр
 Y=0
(27)
Y=0
(27)
(13)
Г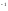 (A)
(A)
 пр
пр Y (28)
Y (28)
(14)
Г (пр
(пр Y)=
пр
Y)=
пр Y (29)
Y (29)
(15)
пр
 Y
Y A
A Г
Г (A)=
пр
(A)=
пр Y (30)
Y (30)
(16)
Г (0)
=0 (31)
(0)
=0 (31)
(17)
Г (A)
= пр
(A)
= пр [(X
[(X A)
A)
 Y]
(32)
Y]
(32)
(18)
(Г
 )
) (A)
= Г
(A)
= Г (
(
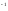 (A)) (33)
(A)) (33)
(19)
(Г
 Г
Г
 …
… Г
Г )
) (A)=
Г
(A)=
Г
 (
Г
(
Г
 …(
Г
…(
Г
 (A))…)
(34).
(A))…)
(34).
Пример
5).
Если M {a,
b,
c,
d,
e,
g}
{a,
b,
c,
d,
e,
g}
Y {<a,
e>, <c, b>, <d, d>, <e, c>, <g, b>, <a,
d>}.
{<a,
e>, <c, b>, <d, d>, <e, c>, <g, b>, <a,
d>}.
Г <Y,
M, M> , X=M, Y=M.
<Y,
M, M> , X=M, Y=M.
A {a,
b, d, g},то
Г
{a,
b, d, g},то
Г (A)
= пр
(A)
= пр [(
X
[(
X A)
A) Y]=
пр
Y]=
пр [{<a,
a>, <a, b>, <a, d>, <a,g>, <b, a>, <b,
b>, <b, d>, <b, g>, <c, a>, <c, b>, <c,
d>, <c, g>, <d, a>, <d,b>, <d, d>, <d,
g>, <e, a>, <e, b>, <e, d>, <e, g>, <g,
a>, <g, b>, <g, d>, <g,g>}
[{<a,
a>, <a, b>, <a, d>, <a,g>, <b, a>, <b,
b>, <b, d>, <b, g>, <c, a>, <c, b>, <c,
d>, <c, g>, <d, a>, <d,b>, <d, d>, <d,
g>, <e, a>, <e, b>, <e, d>, <e, g>, <g,
a>, <g, b>, <g, d>, <g,g>}
 {<a, e>, <c, b>, <d, d>, <e, c>, <g, b>,
<a, d>}] =пр
{<a, e>, <c, b>, <d, d>, <e, c>, <g, b>,
<a, d>}] =пр [{<c,
b>, <d, d>, <g, b>, <a, d>}] = {c, d, g, a}.
[{<c,
b>, <d, d>, <g, b>, <a, d>}] = {c, d, g, a}.
Утверждение
(23), (24) показывает, что Г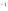 ({a})-
это множество элементов, которым
соответствует в соответствии элемент
а, или графически – множество начал
строк, входящих в а;
({a})-
это множество элементов, которым
соответствует в соответствии элемент
а, или графически – множество начал
строк, входящих в а;
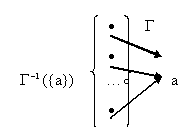
Г (A)
– это множество начал строк, проведенных
к элементам множества А.
(A)
– это множество начал строк, проведенных
к элементам множества А.

Равенство
(32) выражает полный прообраз Г (A)
множества А при соответствии Г через
график соответствия Г.
(A)
множества А при соответствии Г через
график соответствия Г.
Введем еще два новых понятия.
1)
Пусть Г <Y,
M,
M>
- произвольное соответствие, А- произвольное
множество.
<Y,
M,
M>
- произвольное соответствие, А- произвольное
множество.
Тогда
сужением
соответствия Г
на множестве А называется и через Г обозначается соответствием: Г
обозначается соответствием: Г
 <Y
<Y (A
(A Y),
X,Y> (35).
Y),
X,Y> (35).
Таким
образом элемент b
соответствует элементу а в соответствии
Г тогда и только тогда, когдаa
тогда и только тогда, когдаa A
и элемент b
соответствует элементу а в соответствии
Г.
A
и элемент b
соответствует элементу а в соответствии
Г.
График
сужения соответствия Г на множество A
является, по определению (Y (A
(A Y)),
множествам тех пар из графика соответствия
Г, первая компонента которых принадлежит
A.
Y)),
множествам тех пар из графика соответствия
Г, первая компонента которых принадлежит
A.
Область
отправления и область прибытия
соответствия Г совпадают, соответственно, с областью
отправления и областью прибытия
соответствия Г.
совпадают, соответственно, с областью
отправления и областью прибытия
соответствия Г.
Пример 6).


Г <{
<{![]() },
{
},
{
 },
{
},
{ }>.
}>.
A {a,
c}.
{a,
c}.
Г =?
=?


Г =<Y
=<Y (А
(А Y),X,Y>=<Y
Y),X,Y>=<Y
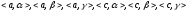 },X,Y>=
=<{
},X,Y>=
=<{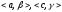 },
}, ,
,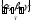 >.
>.
Пример 7).
Г <{<x,
y>
<{<x,
y> D
D |
y=x
|
y=x },
D,
D>,
D-
множество действительных чисел.
},
D,
D>,
D-
множество действительных чисел.
A [2,
3].
[2,
3].

Г
 =?
=?
Г
 =
<Y
=
<Y (А
(А Y),
X,Y
>= <Y
Y),
X,Y
>= <Y [2,
3]
[2,
3] D,
D,
D>=
<[4, 9], D,
D>.
D,
D,
D>=
<[4, 9], D,
D>.
Легко
видеть, что область определения сужения
соответствия Г на множество А равна
(А пр
пр Y).
Y).
Из
(17) имеем: Г(А)= пр [
(А
[
(А Y)
Y)
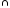 Y].
Следовательно, область значений сужения
соответствия Г на множество А равна
образу множества А при соответствии Г.
Y].
Следовательно, область значений сужения
соответствия Г на множество А равна
образу множества А при соответствии Г.
Если
пр Y
Y А,
то Г
А,
то Г
 =Г.
=Г.
II. Двойственным, в некотором смысле, к понятию сужения является понятие продолжения.
Соответствие

 <H,
Z,
U>
называется продолжением
соответствия Г и элемент b
соответствует элементу а в соответствии
Г, то элемент b
соответствует элементу а и в соответствии
<H,
Z,
U>
называется продолжением
соответствия Г и элемент b
соответствует элементу а в соответствии
Г, то элемент b
соответствует элементу а и в соответствии
 .
.
Для
любых соответствиях Г и множества А
соответствия Г является продолжением
сужения Г
 .
.
Однако
не верно утверждать, что произвольное
соответствие Г <Y,
X,
Y>
равно сужению на пр
<Y,
X,
Y>
равно сужению на пр Y
любого своего продолжения.
Y
любого своего продолжения.
Задачи
Чему рано число соответствий между m- элементным множеством X и n- элементным множеством Y?
X {x
{x ,
… , x
,
… , x }
}
Y {y
{y ,
… , y
,
… , y }.
}.
Г= <Y, X, Y>, где Y
 X
X Y.
Y. =
m
=
m n.
n.Виды графиков Y
 ={
={ }
}
Получим
матрицу размерности m n:
n:

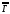 =
= числаk
элементных множеств (графиков Y
числаk
элементных множеств (графиков Y )
из общего числа графиков
)
из общего числа графиков
 =m
=m n.
n.
Вид
графиков Y :
{<x
:
{<x ,
y
,
y >}
>}
{<x ,
y
,
y >,
<x
>,
<x ,
y
,
y >}
>}
…………………….
{<x ,
y
,
y >,
….. , <x
>,
….. , <x ,
y
,
y >}
>}
 =
= C
C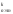 =
=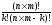 .
.
Доказать или опровергнуть, что для любого соответствия Г и любых множеств А и B:
а).
Г(А B)
= Г(А)
B)
= Г(А)
 Г(B).
Г(B).
Решение
: Г(А)
= пр [(A
[(A Y)
Y) Y] (1)
Y] (1)
Г(B)
= пр [(B
[(B Y)
Y) Y] (2)
Y] (2)
Г (A
(A B)
=пр
B)
=пр [((A
[((A B)
B) Y)
Y) Y] (3).
Y] (3).
пр [(
A
[(
A B)
B) Y]
=пр
Y]
=пр [{<a
[{<a b,y>}
b,y>} Y]
= пр
Y]
= пр [{<a,y>}
[{<a,y>} Y]
Y]
 пр
пр [{<b,
y>}
[{<b,
y>} Y].
Справедливо
Y
Y].
Справедливо
Y
 .
.
b).
Г(A B)
= Г(A)
B)
= Г(A)
 Г(B).
Г(B).
пр [((A
[((A B)
B) Y)
Y) Y]
= пр
Y]
= пр [(A
[(A Y)
Y) Y]
Y] пр
пр [(B
[(B Y)
Y) Y].
Y].
Доказать, что для произвольного соответствия Г и для любого множества А:
 Г
Г (А)
= Г(А).
(А)
= Г(А).
Г(А)=
пр [(A
[(A Y)
Y) Y].
Y].
Г =
<Y
=
<Y (A
(A Y),
X, Y>.
Y),
X, Y>.
Г (А)
= пр
(А)
= пр [(A
[(A Y)
Y) Y
Y (A
(A Y)]
=пр
Y)]
=пр [(
A
[(
A Y)
Y) Y].
Y].
