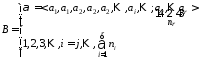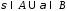Для доказательства (4) докажем импликацию:
![]() при
фиксированном
при
фиксированном
 (5)
(5)
Пусть
имеем

Тогда


![]() ,
что и требовалось доказать.
,
что и требовалось доказать.

А
так как
 -произвольные,
то (4) справедлива, а значит справедливо
и выражение (0).
-произвольные,
то (4) справедлива, а значит справедливо
и выражение (0).
Пример:


1.



2.




3.

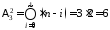

 II.
II.
 -
число перестановок над произвольнымn-элементным
множеством
-
число перестановок над произвольнымn-элементным
множеством
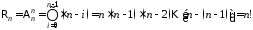
Например:

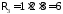

Очевидно:
 .
.
где
 - число
- число -элементных
подмножеств произвольного
-элементных
подмножеств произвольного -
элементного множества
-
элементного множества

§4. Комбинаторные задачи. Перейдем к комбинаторным задачам.
В
комбинаторной задаче обычно требуется
подсчитать, выразить формулой число
элементов некоторого конечного множества

Главным
методом решения такой задачи является
метод установления взаимно-однозначного
соответствия между данным иследуемым
множеством
 и
некоторым вспомогательным множеством
и
некоторым вспомогательным множеством ,
число элементов которого уже известно
,
число элементов которого уже известно
Что такое взаимно-однозначное соответствие?
Если
каждому элементу множества
 поставлениы в соответствие, соотнесен
один элемент множества
поставлениы в соответствие, соотнесен
один элемент множества так, что при этом:
так, что при этом:
разным элементам множества
 поставлены в соответствие разные
элементы множества
поставлены в соответствие разные
элементы множества
каждый элемент множества
 поставлен в соответствие хотя бы одному
элементу множества
поставлен в соответствие хотя бы одному
элементу множества ,
то говорят, что между множествами
,
то говорят, что между множествами и
и установлено взаимно-однозначное
соответствие.
установлено взаимно-однозначное
соответствие.
Очевидно,
что если между двумя конечными множествами
 и
и удалось установить взаимно – однозначное
соответствие, то число элементов
множества
удалось установить взаимно – однозначное
соответствие, то число элементов
множества равно числу элементов множества
равно числу элементов множества

Т.о.
если мы сумеем установить взаимно-однозначное
соответствие между данным множеством
 ,
число элементов которого ищется, и
вспомогательным множеством
,
число элементов которого ищется, и
вспомогательным множеством ,
число элементов которого известно
(скажем, равноt),
то мы решим поставленную задачу, найдем
число элементов множества
,
число элементов которого известно
(скажем, равноt),
то мы решим поставленную задачу, найдем
число элементов множества
 :
оно будет тоже равноt.
:
оно будет тоже равноt.
Решим 2 задачи, имеющие для комбинаторики самостоятельный интерес.
Задача 1.
Пусть
имеется
 r
(различных) объектов (элементов):
r
(различных) объектов (элементов):
 иr
(не обязательно различных) целых
неотрицательных чисел:
иr
(не обязательно различных) целых
неотрицательных чисел:

Обозначим
через
 (ПЭ-протяже
частичное)
(ПЭ-протяже
частичное)
 -
число картежей, имеющих в качестве
компонент:
-
число картежей, имеющих в качестве
компонент:

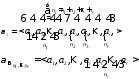
(это так называемые «перестановки с повторениями»)
Т.о., каждый из картежей, число которых мы хотим сосчитать,
имеет
длинну

Докажем,
что




Решение:
Докажем
сначала индукцией по
 ,
что
,
что

а
затем, что

При r = 1 (базис инструкции) правая часть формулы дает

но
очевидно, что число
 картежей, имеющих в качестве компонент,
картежей, имеющих в качестве компонент, раз
– элемент
раз
– элемент ,равно
1 (такой картеж один: это либо пустой
картеж, если
,равно
1 (такой картеж один: это либо пустой
картеж, если =0,
либо картеж
=0,
либо картеж )
)
Т.о., при r = 1 утверждение (2) справедливо.
Допустим
(предположение индукции), что утверждение
(2) верно для некоторого
 ,
и докажем, что оно верно дляr
+ 1, т.е. что число
,
и докажем, что оно верно дляr
+ 1, т.е. что число
 картежей,
имеющую в качестве компонент,
картежей,
имеющую в качестве компонент,

может быть найдено также по закону (2)
Итак,
нам надо доказать, что

Чтобы воспользоваться предположением индукции, «отщипим» от правой части (4) первый множитель. Тогда равенство (4), которое нам надо доказать перепишется в виде:
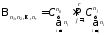
Но по предположению индукции верно (2), следовательно, (5) можно переписать в виде:

Вот в виде-то (6) мы и будем доказывать равенство (4)
Если
 ,
т.е.
,
т.е. ,
утверждение (6) очевидно
,
утверждение (6) очевидно
Пусть
 Обозначим через
Обозначим через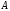 – множество картежей, имеющих в качестве
компонент,
– множество картежей, имеющих в качестве
компонент,

Т.о.,
картежи из А имеют длину

Согласно
нашим обозначениям, число элементов
множества
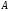 ,
т.е. картежей, равно
,
т.е. картежей, равно
Пусть

Множество
 содержит
содержит элементов.
Элементы множества
элементов.
Элементы множества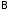 мы будем ниже интерпретировать как
номера компонент картежей из
мы будем ниже интерпретировать как
номера компонент картежей из
Обозначим
через D
множество
 -
элементных подмножеств множества
-
элементных подмножеств множества .
Согласно нашим обозначениям, множествоD
имеет:
.
Согласно нашим обозначениям, множествоD
имеет:
 элементов.
элементов.
Обозначим,
далее, через
 множество картежей, имеющих в качестве
компонент,
множество картежей, имеющих в качестве
компонент,

Т.о.,
картежи из
 имеют длину
имеют длину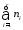 Согласно нашим обозначениям, число
элементов множества
Согласно нашим обозначениям, число
элементов множества равно
равно
Положим,
наконец,
 Как известно, число элементов этого
множества
Как известно, число элементов этого
множества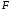 есть
есть

Установим
взаимно-однозначное соответствие между
множествами
 и
и .
Этим равенство (6) будет доказано.
.
Этим равенство (6) будет доказано.
Возьмем
произвольный картеж
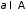 .
Поставим ему в соответствие пару
.
Поставим ему в соответствие пару ,
где
,
где -
множество номеров тех компонент картежа
-
множество номеров тех компонент картежа ,
которые равны
,
которые равны ,
а
,
а - картеж, который получается из
- картеж, который получается из выбрасыванием всех элементов
выбрасыванием всех элементов и стягиванием, с сохранением взаимного
порядка, остальных элементов.
и стягиванием, с сохранением взаимного
порядка, остальных элементов.
Если,
например,
 и
и

то
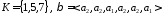
Очевидно,

Итак, мы каждому элементу множества
 поставили в соответствие один элемент
множества
поставили в соответствие один элемент
множества
Докажем теперь, что разные элементы множества
 соответствуют (при нашем соответствии)
разным элементам множества
соответствуют (при нашем соответствии)
разным элементам множества
Пусть
 ,
, и
и .
И даже, пусть картежу
.
И даже, пусть картежу соответствует в
соответствует в при нашем соответствии пара
при нашем соответствии пара ,
картежу
,
картежу -
пара
-
пара
Докажем,
что
 .
Если
.
Если
Пусть
теперь
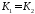 Докажем что тогда
Докажем что тогда
Так
как
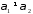 и картежи
и картежи имеют одинаковую длину, по крайней мере
одна из компонент картежа
имеют одинаковую длину, по крайней мере
одна из компонент картежа отлична
от компоненты картежа
отлична
от компоненты картежа с
тем же номером.
с
тем же номером.
Обозначим
через
 любое
такое число, что
любое
такое число, что -я
компонента картежа
-я
компонента картежа отлична
от
отлична
от -й
компоненты картежа
-й
компоненты картежа


Так
как
 ,
, -я
компонента как каретжа
-я
компонента как каретжа ,
так и картежа
,
так и картежа отлична от
отлична от .
Поскольку в картежах
.
Поскольку в картежах левые и правые
левые и правые -е
компоненты одинаковые число элементов
-е
компоненты одинаковые число элементов ,
а на
,
а на -х
местах стоят разные элементы, отличные
от
-х
местах стоят разные элементы, отличные
от ,
,
Докажем, наконец, что каждый элемент множества
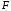 поставлен
нами в соответствие хотя бы одному
элементу множества
поставлен
нами в соответствие хотя бы одному
элементу множества
Пусть
 .
Тогда картежу
.
Тогда картежу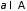 ,
у которого на местах в номерами из
,
у которого на местах в номерами из стоит
стоит ,
а на местах с номерами их
,
а на местах с номерами их стоят в том же порядке компоненты картежа
стоят в том же порядке компоненты картежа ,
соответствует, очевидно, по нашему
закону именно
,
соответствует, очевидно, по нашему
закону именно .
Равенство (6), а значи т и (2) доказано.
.
Равенство (6), а значи т и (2) доказано.
Докажем
теперь утверждение (3). При доказательстве
мы будем опираться на следующие свой
ства оператора

 I.
I.
 (свойство
дроби)
(свойство
дроби)
II.
 (свойство произведения)
(свойство произведения)
III.
 (свойство вычисления
последнего или первого элемента)
(свойство вычисления
последнего или первого элемента)
IV.
 (изменение
пределов оператора)
(изменение
пределов оператора)
Итак, доказательство (3).



Пример.
Пусть




Тогда


Задача 2. «Распределение по ящикам».
Пусть
имеется r
ящиков и r
(не обязателдьно различных) целых
неотрицательных чисел

Пусть
имеется также
 (различных)
предметов.
(различных)
предметов.
Пусть
в 1 ящик можно поместить
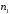 предметов
предметов
Пусть
во 2 ящик можно поместить
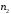 предметов
предметов
Пусть
в r
ящик можно поместить
 предметов
предметов
Найдем
число распределений всех
 данных
предметов по
данных
предметов по ящикам.
При этом два распределения считаются,
естественно различными, если хотя бы
один из данных предметов при одном из
этих распределений находится в одном
ящике, а при другом из этих распределений
– в каком то другом ящике. Оказывается
искомое число равно
ящикам.
При этом два распределения считаются,
естественно различными, если хотя бы
один из данных предметов при одном из
этих распределений находится в одном
ящике, а при другом из этих распределений
– в каком то другом ящике. Оказывается
искомое число равно
Решение.
Надо
ввести какие-то объекты
 и установить взаимно-однозначные
соответствие между множеством
и установить взаимно-однозначные
соответствие между множеством распределений
распределений предметов
по
предметов
по ящикам
вместимостью соответсвенно,
ящикам
вместимостью соответсвенно, и множеством
и множеством картежей, имеющих, в качестве компонент,
картежей, имеющих, в качестве компонент,
 раз
– элемент
раз
– элемент

 раз
– элемент
раз
– элемент
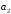
 раз
– элемент
раз
– элемент
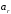
В
качестве объектов
 возьмем числа
возьмем числа .
Пронумеруем данные предметы числами
.
Пронумеруем данные предметы числами
(ящики условием задачи уже предполагаются перенумерованными).
Возьмем
произвольное распределение
 .
Поставим ему в соответствие такой картеж
.
Поставим ему в соответствие такой картеж длины
длины под
под ,
у которого
,
у которого -я
компонента равна
-я
компонента равна тогда и только тогда, когда
тогда и только тогда, когда предмет при распределении
предмет при распределении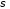 находится в
находится в ящике. Очевидно,
ящике. Очевидно, .
Далее очевидно также, что если
.
Далее очевидно также, что если ,
то для соответствующих картежей
,
то для соответствующих картежей
Можно
видеть, что произвольный картеж
 соответствует в нашем соответствии
такому распределению
соответствует в нашем соответствии
такому распределению
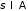 ,
при котором
,
при котором -й
предмет находится в
-й
предмет находится в -м
ящике тогда и только тогда, когда
-м
ящике тогда и только тогда, когда -я
компонента картежа
-я
компонента картежа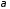 равна
равна (поскольку
(поскольку ,
число, например, 1 имеется в
,
число, например, 1 имеется в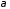 в катчестве компоненты равно
в катчестве компоненты равно раз, и аоэтому ровно
раз, и аоэтому ровно предметов попадут при распределении
предметов попадут при распределении в первый ящик и т.д.).
в первый ящик и т.д.).
Многие комбинаторские задачи укладываются в «схему» двух выше разобранных задач.
Например. Число раздач 36-карточной колоды четырем игрокам по 6 карт, равно, очевидно, числу распределений 36 карт по 5 ящикам вместимостью соответственно 6, 6, 6, 6 и 12 (пятый ящик – оставшиеся карты), т.е. равно
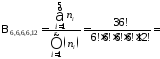

 -
ящики
-
ящики
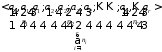 -
предметы
-
предметы