
- •Н.И. Калядин
- •Н.И. Калядин
- •Глава 1. Функции алгебры логики
- •1.1. Основные определения
- •Геометрическое представление фал.
- •2.3 Задачи и упражнения iiIго типа *.
- •1.4 Свойства конъюнкции, дизъюнкции и отрицания.
- •1.5 Свойства сложения по модулю два, импликации и функции Шеффера и Вебба.
- •Алгоритм приведения формулы к днф.
- •Совершенные дизъюнктивные и конъюнктивные нормальные формы.
- •Алгоритм построения скнф.
- •Алгоритм нахождения сднф путем тождественных преобразований
- •Совершенно полиноминальная нормальная форма (спнф).
- •Алгоритм построения спнф.
- •Глава 2. Задания к практическим занятиям, выполнению расчетно-графических работ и для самостоятельной работы по функциям алгебры логики.
- •2.1 Задачи и упражнения iго – типа *.
- •1.8 Методы определения линейности фал.
- •1. Использование таблиц истинности.
- •Замечательное свойство классов фал (классов Поста):
- •1.9 Функционально замкнутые классы. Критерий полноты *.
- •2. Использование полинома Жегалкина.
- •1.7 Основные классы функций алгебры логики
- •Алгоритм построения сднф.
- •2.2 Задачи и упражнения iiго – типа *.
- •1.6 Аналитические формы представления фал. Дизъюнктивные и конъюнктивные нормальные формы
- •1.3 Выражение одних элементарных функций через другие
- •1.2 Элементарные функции алгебры логики
- •Предисловие.
- •Список литературы.
Алгоритм построения сднф.
1. Выбрать в таблице
задания функции все наборы (![]() )
аргументов, на которых
)
аргументов, на которых
![]() .
.
2. Выписать
конституенты единицы ![]() ,
соответствующие этим наборам аргументов;
при этом, если аргумент
,
соответствующие этим наборам аргументов;
при этом, если аргумент
![]() входит
в данный набор как 1, он вписывается без
изменений
входит
в данный набор как 1, он вписывается без
изменений![]() в конъюнкт
в конъюнкт![]() ;
если же
;
если же![]() входит в данный набор как 0, то в
соответствующий конъюнкт вписывается
его отрицание (
входит в данный набор как 0, то в
соответствующий конъюнкт вписывается
его отрицание (![]() ).
).
3. Все полученные конституенты единицы соединяются знаками дизъюнкции.
Пример 1-9.
Найти СДНФ и СКНФ функции
![]() ,
заданной следующей таблицей истинности:
,
заданной следующей таблицей истинности:
|
|
|
|
|
Конституенты:
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
|
(![]() )
– наборы аргументов
)
– наборы аргументов![]() .
.
![]()
![]()
14 27
2.2 Задачи и упражнения iiго – типа *.
1. Проверить полноту заданной системы функций. Для функционально полной системы выделить базис.
1) F={![]() ,
,
![]() },
где
},
где
![]() =x
=x![]() y,
y,
![]() =x
=x![]() ¬yz,
¬yz,
2) F={![]() ,
,![]() ,
,![]() ,
,![]() },
где
},
где
![]() =x¬y,
=x¬y,
![]() =x~yz,
=x~yz,
![]() =0,
=0,
![]() =1,
=1,
3) F={![]() ,
,![]() ,
,![]() ,
,![]() },
где
},
где![]() =(x
=(x![]() y)
y)![]() (y~z),
(y~z),![]() =(x/(xy))
=(x/(xy))![]() z,
z,![]() =x
=x![]() y,
y,
![]() =0,
=0,
4) F={![]() ,
,![]() ,
,![]() },
где
},
где
![]() =(0110
1001),
=(0110
1001),
![]() =(1000
1101),
=(1000
1101),
![]() =(0001
1100)
=(0001
1100)
5) F={![]() ,
,![]() ,
,![]() },
где
},
где
![]() =(0100
0100),
=(0100
0100),
![]() =(1111
1100),
=(1111
1100),
![]() =(1000
0000)
=(1000
0000)
2. Составить все возможные базисы из функций двух переменных.
3. Для заданной
функции
![]() :
:
1) построить таблицу истинности;
2) построить изображение на кубе;
З) найти СДНФ и СКНФ;
4. Определить принадлежность классам Поста.
5. Построить
функционально полную систему функции
так, чтобы эта система была базисом и
содержала
![]() .
.
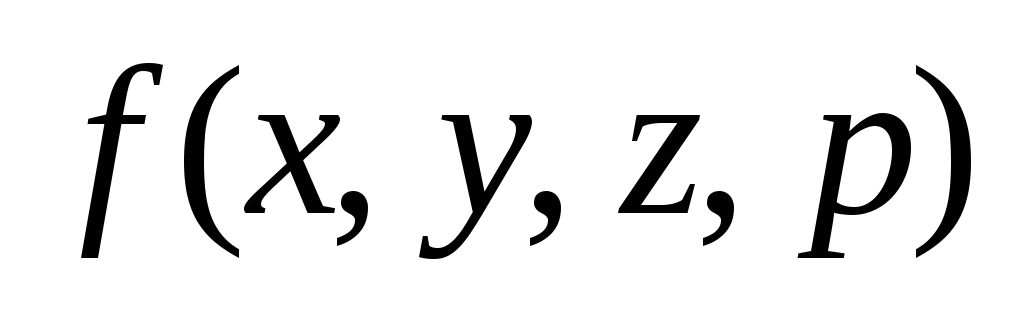 =x
=x p/z
p/z ¬y
¬y x
x p
p z
z x
x y
y z,
z, =p
=p y
y y
y x
x z
z p/y
p/y ¬z
¬z x,
x, ==p/z
==p/z x
x y
y z
z y
y p
p ¬x
¬x y
y z,
z, =y
=y z
z p
p x
x z
z p
p y/¬y
y/¬y z,
z, =z
=z y
y p
p x
x ¬z
¬z p/z
p/z y
y x,
x,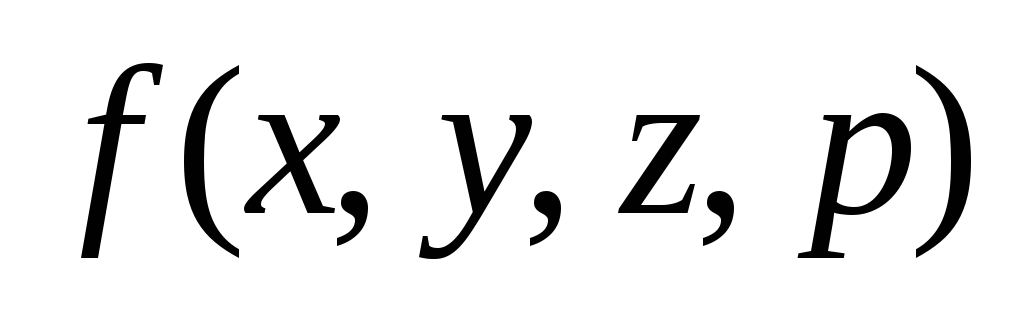 =x
=x y
y p
p x
x z
z x/y
x/y ¬z
¬z x
x z,
z, =z
=z y
y x
x z
z p
p x
x z/y
z/y ¬p,
¬p, =y
=y z
z p
p x
x z
z p
p y/¬p
y/¬p z,
z, =p
=p x
x z
z ¬y
¬y p
p z
z y/z
y/z x,
x, =x/y
=x/y z
z p
p x
x y
y ¬z
¬z p
p y
y z,
z, =z
=z p
p y
y z
z x
x p
p y
y z/¬x,
z/¬x, =¬x/z
=¬x/z p
p y
y x
x z
z p
p z
z p,
p, =x
=x y
y z
z ¬p
¬p x/y
x/y z
z p
p z,
z,
Пусть (![]() )
– набор логических переменных,
)
– набор логических переменных,![]() - набор нулей и единиц.
- набор нулей и единиц.
Конституентой
единиц набора
![]() называется конъюнкт:
называется конъюнкт:
![]() .
.
Конституентой
нуля набора
![]() называется дизъюнкт:
называется дизъюнкт:
![]() .
.
Отметим, что
![]() (
(![]() )
тогда и только тогда, когда
)
тогда и только тогда, когда![]() .
.
Совершенной ДНФ
называется дизъюнкция некоторых
конституент единиц, среди которых нет
одинаковых, а совершенной КНФ называется
конъюнкция некоторых конституент нуля,
среди которых нет одинаковых. Таким
образом, СДНФ (СКНФ) есть ДНФ (КНФ), в
которой в каждой конъюнкт (дизъюнкт)
каждая переменная
![]() из набора (
из набора (![]() )
входит ровно один раз, причем входит
либо сама
)
входит ровно один раз, причем входит
либо сама![]() ,
либо ее отрицание
,
либо ее отрицание![]() .
.
Пример 1-8.
Формула
![]() есть конституента единицы
есть конституента единицы![]() ;
формула
;
формула![]() есть конституента нуля
есть конституента нуля![]() ;
формула
;
формула![]() - СДНФ, формула (
- СДНФ, формула (![]() )
)![]() - СКНФ.
- СКНФ.
Для решения задачи
нахождения СДНФ и СКНФ, эквивалентных
исходной формуле
![]() ,
предварительно рассмотрим разложения
булевой функции
,
предварительно рассмотрим разложения
булевой функции![]() по
по![]() переменным
(для определенности по
переменным
(для определенности по![]() )
–разложения Шеннона.
)
–разложения Шеннона.
Теорема 4 (первая
теорема Шеннона).
Любая булева
функция
![]() представима
в виде разложения Шеннона:
представима
в виде разложения Шеннона:
 .
.
п ри
ри![]() для
булевой функции
для
булевой функции![]() ,получаем
ее представление в виде совершенной
ДНФ:
,получаем
ее представление в виде совершенной
ДНФ:
 .
.
В силу принципа двойственности для булевых алгебр справедлива:
Теорема 5 (вторая
теорема Шеннона). Любая
булева функция
![]() представима
в виде разложения Шеннона:
представима
в виде разложения Шеннона:
12
 =y
=y p
p x
x z
z p
p y/¬p
y/¬p x
x z,
z, =p
=p x
x z
z y
y p/¬z
p/¬z y
y x
x y,
y, =x/p
=x/p y
y x
x ¬p
¬p z
z y
y z
z y,
y, =¬p
=¬p z
z x
x y
y (z
(z p
p x)/y
x)/y p,
p, =z
=z x
x y/x
y/x p
p ¬x
¬x z
z p
p x,
x, =p
=p x
x ¬y
¬y z/p
z/p p
p x
x z
z y,
y, =z/p
=z/p x
x p
p y
y x
x p
p y
y ¬z,
¬z, =p
=p ¬x
¬x z
z y
y p
p z/x
z/x z
z y,
y, =x
=x ¬p
¬p z
z y
y z
z p/x
p/x z
z x,
x, =x
=x z
z ¬p/y
¬p/y z
z p
p y
y x
x z,
z, =¬x
=¬x z
z p
p ¬y/x
¬y/x p
p x
x y
y z,
z, =y
=y p
p x/z
x/z y
y p
p x
x z
z ¬x,
¬x, =p
=p x
x y/z
y/z p
p x
x ¬z
¬z y
y z,
z, =x
=x y
y z
z ¬p
¬p z
z y/z
y/z p
p x,
x, =y/z
=y/z x
x p
p x
x z
z y
y ¬z
¬z p,
p, =x
=x y
y z
z x
x y
y p
p z
z ¬y/x,
¬y/x, =z
=z p
p x
x (p
(p z)/z
z)/z y
y p
p ¬x,
¬x, =p/x
=p/x z
z y
y x
x p
p ¬z
¬z y
y x,
x, =¬x
=¬x y
y z
z p
p x
x y
y z/p
z/p x,
x, =z
=z p
p x
x y
y z
z p
p x
x y/¬x,
y/¬x, =¬p
=¬p x
x z
z y/p
y/p x
x y
y p
p x,
x, =y
=y x
x ¬z
¬z p/y
p/y x
x p
p z,
z, =y
=y x
x y
y p
p z/x
z/x ¬y
¬y x
x z,
z,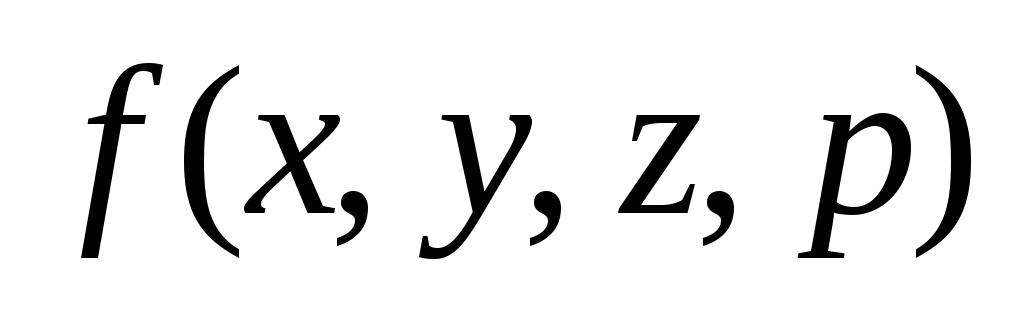 =x
=x y
y z
z ¬p
¬p x
x z
z y
y p/x,
p/x, =z/y
=z/y p
p x
x y
y ¬z
¬z x
x p
p y,
y, =y
=y x
x p
p ¬z
¬z x
x y/z
y/z p
p z,
z, =p
=p x
x z
z y
y ¬x
¬x z/p
z/p y
y x,
x, =x
=x y
y z
z p/x
p/x ¬y
¬y z
z p
p x,
x,
29
=x y
y z
z p/x
p/x ¬y
¬y z
z p
p x,
x,
Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:
 (1 – 19)
(1 – 19)
Для функций Шеффера и Вебба имеет место переместительный закон:
![]() ;
;
![]() .
.
Сочетательный закон для них несправедлив:
![]() ;
;
![]()
Имеют место следующие очевидные соотношения:
 (1 – 20)
(1 – 20)
Выражение функции
Шеффера и Вебба в базисе {![]() }:
}:
 (1 – 21)
(1 – 21)
Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулам де Моргана для функций конъюнкции и дизъюнкции:
 (1 – 22)
(1 – 22)
