2. Использование полинома Жегалкина.

Линейность ФАЛ можно определить с помощью разложения в полином Жегалкина в базисе.

Теорема 7. Всякая ФАЛ представима полиномом Жегалкина:

, (1 – 25)

где в каждом наборе всеразличны, а суммирование ведется по некоторому множеству таких несовпадающих наборов. Представление ФАЛ в виде полинома Жегалкина единственно с точностью до порядка слагаемых.

Полином Жегалкина называется нелинейным (линейным), если он (не) содержит произведения переменных.

(1 – 26)

Линейность ФАЛ равносильна линейности соответствующего полинома Жегалкина.

Для получения полинома Жегалкина заданной ФАЛ необходимо представить функцию в СДНФ, а далее применить эквивалентности:

Пример 1-13. Записать в виде полинома Жегалкина функцию:

18

16. Показать неполноту следующих систем функций и сделать выводы о существенности условий теоремы Поста:

а) 0,,; б) 1,,; в); г)0, 1,;

д) 0,1,

17. Доказать, что ни один из классов не содержится в другом.

18. Доказать, что всякий собственный функционально замкнутый класс содержится в одном из классов .

19. Доказать, что функционально замкнутые классыявляются предполными и других предполных классов нет.

Теорема Поста позволяет выяснить вопрос о том, является ли полная система базисом. Это удобно делать при помощи таблиц Поста.

Сделаем некоторые общие замечания о базисах, следующие из теоремы Поста. Начнем с наиболее простого:

20. Доказать, что базис не может содержать более пяти функций.

На самом деле имеет место более точный результат.

21. Доказать, что базис не может содержать более четырех функций.

В силу задач 2 и 9 существуют базисы с любым числом функций, не превосходящим четырех.

22. Доказать, что из всякого базиса можно отождествлением аргументов у входящих в него функций получить базис, в котором все функции зависят не более чем от трех переменных; дальнейшее уменьшение числа переменных, вообще говоря, невозможно.

Определение 14. Если при любом отождествлении переменных у всякой функции базиса получаем неполную систему, то базис называется минимальным.

23. Доказать, что имеется конечное число различных минимальных базисов.

Оказывается, что это число равно 48.

Исследуем некоторые специальные типы базисов. Начнем с базисов, состоящих из одной функции.

Определение 15. Функция алгебры логики, представляющая собой базис из одного элемента, называется обобщенной функцией Шеффера.

24. Сколько имеется обобщенных функций Шеффера отпеременных?

25. Найти все минимальные базисы из одной функции.

Теперь, напротив, рассмотрим базисы, содержащие максимально возможное число функций.

26. Какой может быть таблица Поста для базиса из четырех функций?

27. Найти все минимальные базисы из четырех функций.

23

Пример 1-11. Найти в СПНФ по исходной СДНФ.

Окончательно после раскрытия скобок и сокращения одинаковых слагаемых, входящих четное число раз, имеем .

1.7 Основные классы функций алгебры логики

Для решения ряда принципиальных вопросов, связанных с теорией ФАЛ и с практическим применением результатов этой теории для анализа и синтеза схем, полезно рассмотреть основные классы ФАЛ (классы Поста).

1. -класс функций, сохраняющих константу нуль, т. е. таких функций, для которых имеет место равенство: .

В таблице 1 класс . Очевидно, что при фиксированномn число функций этого класса составляет половину всех функций алгебры логики, т. е. функций.

2. -класс функций, сохраняющих константу единица, будет определен как класс функций, для которых имеет место равенство: .

В таблице 1 класс . Этот класс также состоит изфункции.

Определение 4. Функция называется двойственной к функции, если имеет место равенство.

=

Определение 5. Функция называется самодвойственной, если она совпадает с двойственной себе функцией, т. е. имеет место равенство:

=

3.-класс самодвойственных функций. В таблице 1 класс .

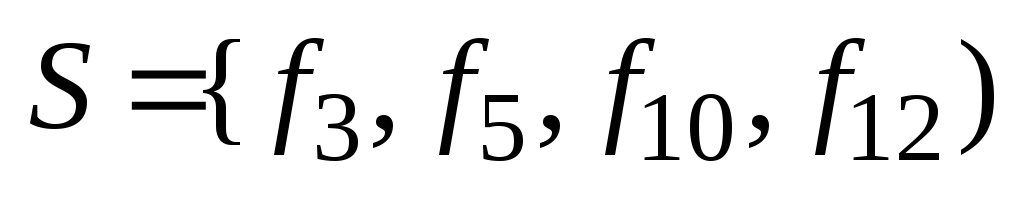Число членов этого класса равно , так как самодвойственная функция отn аргументов полностью определяется на половине наборов значений аргументов.

Б

16

удем говорить, что набор значений аргументане меньше набора значений аргументов, т.е., если

11. Разработать тест распознавания противоречивого задания недоопределенной булевой функции (функция заданапротиворечиво, если () ()).

12. Найти минимальную ДНФ булевой функции

13. Определить скобочную форму булевой функции

14. Найти мощность единичной области недоопределенной булевой функции после ее доопределения:

15. Проверить линейность булевой функции

16. Установить, является ли самодвойственной функция эквивалентности.

17. Проверить монотонность конъюнкции от n аргументов.

18. Привести пример монотонной функции, которая одновременно была бы линейной.

19. Привести пример самодвойственной функции, которая одновременно была бы линейной.

20. Привести пример линейной и монотонной функций.

21. Убедиться, что функции Шеффера и Вебба не являются ни линейными, ни монотонными, ни самодвойственными.

22. Установить, образует ли булева функции

базис в .

2З. Верно ли утверждение: если булева функция существенно зависит более чем от одного аргумента и она монотонна, то она несамодвойственна?

24. Верно ли утверждение: если булева функция существенно зависит более чем от одного аргумента и она линейна, то она немонотонна?

25. Найти все булевы функции, удовлетворяющие системе уравнений

26. Доказать следующую теорему: при суперпозиции линейных функций получаются линейные функции.

2

25

7. Доказать теорему: при суперпозиции самодвойственных функций вновь получаются самодвойственные функции.