
- •Основы теории алгоритмов и нумераций
- •Оглавление
- •Введение*
- •Глава 1. Рекурсивные и примитивно-рекурсивные функции
- •Обозначения
- •Примитивно рекурсивные функции
- •Примеры
- •Функции Аккермана
- •Примеры
- •Общерекурсивные и частично рекурсивные функции
- •Глава 2. Машины тьюринга
- •Определения
- •Табличноеиграфическоезадания машинТьюринга
- •Графическое представление
- •Табличное значение машины
- •Некоторые операции над машинами Тьюринга
- •Композиция машин Тьюринга
- •Разветвление машин Тьюринга
- •Универсальная машина Тьюринга
- •Тезис Черча. Связь рекурсивных функций с машинами Тьюринга
- •Примеры
- •Глава 3. Вычислимость и разрешимость
- •Обсуждение
- •Нумерации алгоритмов
- •Некоторые теоремы в теории алгоритмов.
- •Глава 4. Рекурсивные и рекурсивно перечислимые множества.
- •Характеристические функции множеств.
- •Рекурсивные и примитивно рекурсивные множества.
- •Рекурсивно перечислимые множества.
- •Основная теорема.
- •Примеры.
- •Глава 5. Основные нумерации в теории алгоритмов
- •Нумерация пар и-ок чисел.
- •Кодирование всех-ок.
- •Нумерация конечных множеств.
- •Нумерации Клини и Поста.
- •Нумерация семейства всех двухэлементных множеств.
- •Глава 6. Степени неразрешимости.
- •- Сводимость.
- •- Степени.
- •Теорема о редукции.
- •Примеры.
- •Глава 7. Нумерованные совокупности.
- •Нумерации множества.
- •Некоторые теоремы о нумерациях множеств
- •Глава 8. Приложения теории алгоритмов к разрешимости некоторых проблем.
- •Теорема Райса.
- •Разрешимость проблем распознавания и классификации.
- •Литература
- •Основы теории алгоритмов и нумераций.
Глава 2. Машины тьюринга
Определения
Машина Тьюринга полностью определяется:
внешним алфавитом
 ,
(где
,
(где ,
, );
);алфавитом внутренних состояний
 ;
;программой, то есть совокупностью выражений
 ,
каждое из которых имеет один из следующих
видов:
,
каждое из которых имеет один из следующих
видов: ,
где
,
где .
Выражения
.
Выражения называютсякомандами.
называютсякомандами.
Машинным словомиликонфигурациейназывается слово вида![]() ,
где
,
где![]() ,
,![]() ,
,![]() и
и![]() - слова (возможно пустые) в алфавите
- слова (возможно пустые) в алфавите![]() .
Пишем
.
Пишем![]() для сокращения слова
для сокращения слова![]() .
.
Пусть даны машина
![]() и машинное слово
и машинное слово![]() ,
где
,
где![]() .
Обозначим через
.
Обозначим через![]() слово, которое получается из
слово, которое получается из![]() по правилам:
по правилам:
для
 положим
положим ;
;для
 :
:если
 имеет вид
имеет вид ,
то
,
то ;
;если
 имеет вид
имеет вид ,
то
,
тоесли
 не пусто, то
не пусто, то ,
,если
 пусто, то
пусто, то ;
;
если
 имеет вид
имеет вид ,
то
,
тоесли
 ,
для некоторых
,
для некоторых и
и ,
то
,
то ;
;если
 пусто, то
пусто, то .
.
Положим
![]() .
.
Говорим, что машина
![]() перерабатывает машинное слово
перерабатывает машинное слово![]() в слово
в слово![]() ,
если
,
если![]() для некоторого
для некоторого![]() .
Пишем
.
Пишем![]() ,
если машина
,
если машина![]() перерабатывает слово
перерабатывает слово![]() в
в![]() и при этом не используется пункт (в2)
определения.
и при этом не используется пункт (в2)
определения.
Пишем
![]() ,
если машина
,
если машина![]() перерабатывает слово
перерабатывает слово![]() в
в![]() и при этом не используются пункты (б2)
и (в2).
и при этом не используются пункты (б2)
и (в2).
Говорим, что машина
![]() вычисляет
вычисляет![]() - местную частичную числовую функцию
- местную частичную числовую функцию![]() ,
где
,
где![]() ,
,![]() ,
если выполнены следующие условия:
,
если выполнены следующие условия:
если
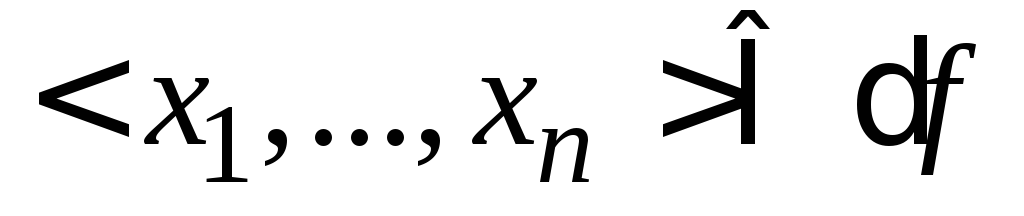 ,
то машина
,
то машина останавливается, то есть перерабатывает
слово
останавливается, то есть перерабатывает
слово в некоторое слово
в некоторое слово ,
и при этом слово
,
и при этом слово ,
содержит
,
содержит вхождение символа
вхождение символа ;
;если
 ,
то машина, начиная работу со слова
,
то машина, начиная работу со слова ,
работает бесконечно.
,
работает бесконечно.
Говорим, что машина
![]() правильно вычисляет функцию
правильно вычисляет функцию![]() ,
если выполнены условия:
,
если выполнены условия:
если
 ,
то
,
то ,
,если
 ,
то машина, начиная работу со слова
,
то машина, начиная работу со слова ,
работает бесконечно.
,
работает бесконечно.
Функция
![]() называется вычислимой (правильно
вычислимой), если существует машина,
которая вычисляет (правильно вычисляет)
эту функцию.
называется вычислимой (правильно
вычислимой), если существует машина,
которая вычисляет (правильно вычисляет)
эту функцию.
Табличноеиграфическоезадания машинТьюринга
Машины Тьюринга содержат:
управляющее устройство, которое может находится в одном из состояний, образующих конечное множество
 ;
;ленту, разбитую на ячейки, в каждой из которых может быть записан один из символов конечного алфавита
 ;
;устройство обращения к ленте, т.е. считывающую и пишущую головку, которая в конечный момент времени обозревает ячейку ленты в зависимости от символа в этой ячейке и состояния управляющего устройства, записывает в ячейку символ (быть может, совпадающий с прежним или пустой, т.е. стирает символ), сдвигает на ячейку влево или вправо или остается на месте; при этом управляющее устройство переходит в новое состояние (или остается в старом). Среди состояний начального устройства выделяют начальное состояние
 и заключительное состояние
и заключительное состояние .
В начальном состоянии машина находится
перед началом работы, попав в заключительное
состояние, машина останавливается.
.
В начальном состоянии машина находится
перед началом работы, попав в заключительное
состояние, машина останавливается.
Таким образом, память машины Тьюринга
- это конечное множество состояний
(внутренняя память) и лента (внешняя
память). Лента бесконечна в обе стороны,
однако в начальный момент времени только
конечное число ячеек ленты заполнено
непустыми словами, остальные ячейки
пусты; т.е. содержат пустой символ
![]() (пробел). Из характера работы машины
следует, что и в любой последующий момент
времени лишь конечный отрезок ленты
будет заполнен символами. Поэтому важна
не фактическая (как говорят в математике,
актуальная) бесконечность ленты, а ее
неограниченность, т.е. возможность иметь
на ней сколь угодно длинные, но конечные
слова. Данные машины Тьюринга - это слова
в алфавите ленты, на ленте записываются
и исходные данные, и окончательные
результаты. Элементарные шаги машины
- это считывание и запись символов, сдвиг
головки на ячейку влево, вправо, а также
переход управляющего устройства в
следующее состояние. Детерменированность
машины, т.е. последовательность ее шагов,
определяется следующим образом: для
любого внутреннего состояния
(пробел). Из характера работы машины
следует, что и в любой последующий момент
времени лишь конечный отрезок ленты
будет заполнен символами. Поэтому важна
не фактическая (как говорят в математике,
актуальная) бесконечность ленты, а ее
неограниченность, т.е. возможность иметь
на ней сколь угодно длинные, но конечные
слова. Данные машины Тьюринга - это слова
в алфавите ленты, на ленте записываются
и исходные данные, и окончательные
результаты. Элементарные шаги машины
- это считывание и запись символов, сдвиг
головки на ячейку влево, вправо, а также
переход управляющего устройства в
следующее состояние. Детерменированность
машины, т.е. последовательность ее шагов,
определяется следующим образом: для
любого внутреннего состояния![]() и символа
и символа![]() однозначно заданы:
однозначно заданы:
следующее состояние
 ;
;символ
 ,
который нужно записать вместо
,
который нужно записать вместо в ту же ячейку (стирание символа будем
понимать как запись пустого символа
в ту же ячейку (стирание символа будем
понимать как запись пустого символа );
);направление сдвига головки обозначалось одним из трех символов
 (влево),
(влево), (вправо),
(вправо), (на месте). Это задание может записываться
либо системой правил (команд), имеющих
вид
(на месте). Это задание может записываться
либо системой правил (команд), имеющих
вид
![]()
![]() ,
,
либо таблицей,
строкам которой соответствуют состояния,
столбцам - входные символы, а на пересечении
строки и столбца записана тройка символов
![]() ,
и, наконец, блок-схемой, которую будем
называть диаграммой переходов. В этой
диаграмме состояниям соответствуют
вершины, а правилу вида
,
и, наконец, блок-схемой, которую будем
называть диаграммой переходов. В этой
диаграмме состояниям соответствуют
вершины, а правилу вида![]() - ребро. Условие однозначности требует,
чтобы для любого
- ребро. Условие однозначности требует,
чтобы для любого![]() и любого
и любого![]() в системе команд имелась одна команда,
аналогична
в системе команд имелась одна команда,
аналогична![]() с левой частью
с левой частью![]() ;
состояние
;
состояние![]() в левых частях команд не встречается.
в левых частях команд не встречается.
Такое состояние машины Тьюринга, по
которому однозначно можно определить
ее дальнейшее поведение, определяется
ее внутренним состоянием, состоянием
ленты (т.е. словом, записанным на ленте)
и положением головки на ленте. Полное
состояние будет называться конфигурацией
или машинным словом и обозначаться
тройкой
![]() ,
где
,
где![]() - текущее внутреннее состояние;
- текущее внутреннее состояние;![]() - слово слева от головки и
- слово слева от головки и![]() - слово, образованное символом обозреваемой
ячейки головкой и символами справа от
него, причем слева от
- слово, образованное символом обозреваемой
ячейки головкой и символами справа от
него, причем слева от![]() и справа от
и справа от![]() нет пустых символов.
нет пустых символов.
Стандартной начальной конфигурациейназовемконфигурациювида![]() ,
т.е. конфигурацию, содержащую начальное
состояние, в которой головка обозревает
крайний левый символ слова, написанного
на ленте. Аналогичностандартной
заключительной конфигурациейназовемконфигурациювида
,
т.е. конфигурацию, содержащую начальное
состояние, в которой головка обозревает
крайний левый символ слова, написанного
на ленте. Аналогичностандартной
заключительной конфигурациейназовемконфигурациювида![]() .
Ко всякой не заключительной конфигурации
.
Ко всякой не заключительной конфигурации![]() машины
машины![]() применима лишь одна команда вида
применима лишь одна команда вида![]() ,
которая конфигурацию
,
которая конфигурацию![]() переводит в конфигурацию
переводит в конфигурацию![]() .
Это отношение между конфигурациями
обозначим
.
Это отношение между конфигурациями
обозначим![]() .
.
Последовательность конфигураций
![]() однозначно определяется исходной
конфигурацией
однозначно определяется исходной
конфигурацией![]() и полностью описывает работу машины
и полностью описывает работу машины![]() ,
начиная с
,
начиная с![]() .
Она конечна, если в ней встретится
заключительная конфигурация (содержащая
.
Она конечна, если в ней встретится
заключительная конфигурация (содержащая![]() )
и бесконечна в противном случае.
)
и бесконечна в противном случае.
Пример 1. Машина с алфавитом![]() ,
состояниями
,
состояниями![]() и системой команд
и системой команд![]() из любой конфигурации будет работать
бесконечно, заполняя единицами всю
ленту вправо от начальной точки.
из любой конфигурации будет работать
бесконечно, заполняя единицами всю
ленту вправо от начальной точки.
Пример 2. Сложение![]() .
.
Сложить числа
![]() и
и![]() - это значит слово
- это значит слово![]() переработать в слово
переработать в слово![]() ,
т.е. удалить разделитель и сдвинуть один
из слагаемых, первое к другому. Это
преобразование осуществляет машина
,
т.е. удалить разделитель и сдвинуть один
из слагаемых, первое к другому. Это
преобразование осуществляет машина![]() с четырьмя составляющими и следующей
системой команд (первая команда введена
для случая, когда
с четырьмя составляющими и следующей
системой команд (первая команда введена
для случая, когда![]() и исходное слово имеет вид
и исходное слово имеет вид![]() ):
):

В этой системе команд перечислены не все сочетания состояний машины и символов ленты. Опущены те из них, которые при стандартной начальной конфигурации никогда не встретятся. В таблице 1 это будет отмечено прочерками.
