
- •Основы теории алгоритмов и нумераций
- •Оглавление
- •Введение*
- •Глава 1. Рекурсивные и примитивно-рекурсивные функции
- •Обозначения
- •Примитивно рекурсивные функции
- •Примеры
- •Функции Аккермана
- •Примеры
- •Общерекурсивные и частично рекурсивные функции
- •Глава 2. Машины тьюринга
- •Определения
- •Табличноеиграфическоезадания машинТьюринга
- •Графическое представление
- •Табличное значение машины
- •Некоторые операции над машинами Тьюринга
- •Композиция машин Тьюринга
- •Разветвление машин Тьюринга
- •Универсальная машина Тьюринга
- •Тезис Черча. Связь рекурсивных функций с машинами Тьюринга
- •Примеры
- •Глава 3. Вычислимость и разрешимость
- •Обсуждение
- •Нумерации алгоритмов
- •Некоторые теоремы в теории алгоритмов.
- •Глава 4. Рекурсивные и рекурсивно перечислимые множества.
- •Характеристические функции множеств.
- •Рекурсивные и примитивно рекурсивные множества.
- •Рекурсивно перечислимые множества.
- •Основная теорема.
- •Примеры.
- •Глава 5. Основные нумерации в теории алгоритмов
- •Нумерация пар и-ок чисел.
- •Кодирование всех-ок.
- •Нумерация конечных множеств.
- •Нумерации Клини и Поста.
- •Нумерация семейства всех двухэлементных множеств.
- •Глава 6. Степени неразрешимости.
- •- Сводимость.
- •- Степени.
- •Теорема о редукции.
- •Примеры.
- •Глава 7. Нумерованные совокупности.
- •Нумерации множества.
- •Некоторые теоремы о нумерациях множеств
- •Глава 8. Приложения теории алгоритмов к разрешимости некоторых проблем.
- •Теорема Райса.
- •Разрешимость проблем распознавания и классификации.
- •Литература
- •Основы теории алгоритмов и нумераций.
Примеры
Доказать, что если функция
 примитивно рекурсивна, то следующие
функции примитивно рекурсивны:
примитивно рекурсивна, то следующие
функции примитивно рекурсивны: (перестановка
аргументов);
(перестановка
аргументов); (циклическая
перестановка аргументов);
(циклическая
перестановка аргументов); (введение фиктивного
аргумента);
(введение фиктивного
аргумента); (отождествление
аргументов).
(отождествление
аргументов).
Доказать, что следующие функции примитивно рекурсивны:


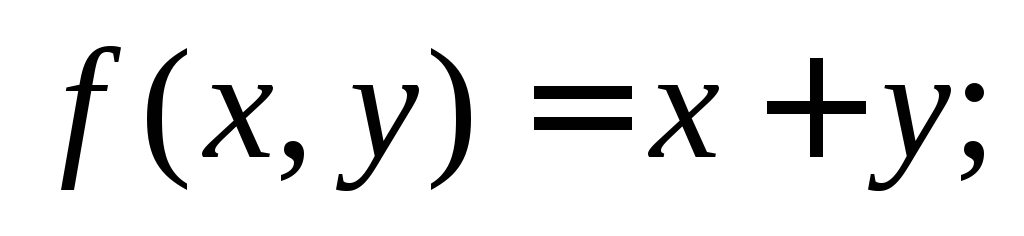

 (здесь
(здесь
 );
); (здесь
(здесь
 ).
).
Доказать, что следующие функции примитивно рекурсивны:
 ,
где
,
где
 - сигнум или знак
- сигнум или знак


 ∸
∸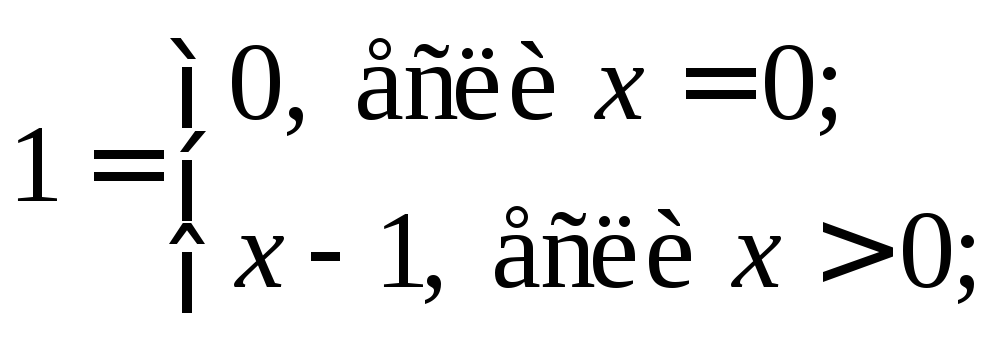
 ∸
∸



Доказать следующие равенства:
 ∸
∸ ∸
∸
 ∸
∸ ∸
∸
 ∸
∸ ∸
∸ ∸
∸
 ∸
∸ ∸
∸ ∸
∸ ∸
∸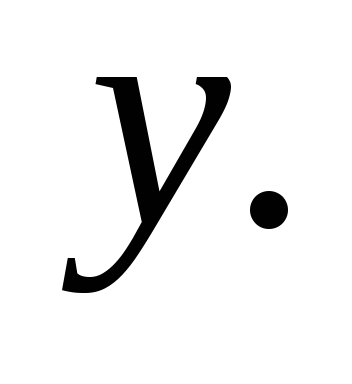
Доказать, что если
 получается
из примитивно рекурсивных функций
получается
из примитивно рекурсивных функций и
и с
помощью ограниченного
с
помощью ограниченного - оператора, то
- оператора, то -
примитивно рекурсивна.
-
примитивно рекурсивна.Доказать, что если
 получается из примитивно рекурсивных
функций
получается из примитивно рекурсивных
функций и
и с помощью ограниченного
с помощью ограниченного - оператора, то
- оператора, то - примитивно рекурсивная.
- примитивно рекурсивная.
Функции Аккермана
Пора уже задать вопрос: все ли функции
являются примитивно рекурсивными?
Простые теоретико-множественные
соображения показывают, что нет. Множество
функций типа
![]() несчетно, тем более это верно для функций
типа
несчетно, тем более это верно для функций
типа![]() .
Каждая примитивно рекурсивная функция
имеет конечное описание, то есть задается
конечным словом в некотором (фиксированным
для всех функций) алфавите. Множество
всех конечных слов счетно, поэтому
примитивно рекурсивные функции образуют
не более чем счетное подмножество
несчетного множества функций типа
.
Каждая примитивно рекурсивная функция
имеет конечное описание, то есть задается
конечным словом в некотором (фиксированным
для всех функций) алфавите. Множество
всех конечных слов счетно, поэтому
примитивно рекурсивные функции образуют
не более чем счетное подмножество
несчетного множества функций типа![]() .
.
В действительности здесь рассматривается более узкий вопрос, все ли вычислимые функции можно записать как примитивно рекурсивные? Чтобы показать, что ответ на этот вопрос также является отрицательным, построим пример вычислимой функции, не являющейся примитивно рекурсивной. Идея примера в том, чтобы построить последовательность функций, каждая из которых растет существенно быстрее предыдущей, сконструировать с ее помощью функцию, которая растет быстрее любой примитивно рекурсивной функции.
Начнем с построения последовательности
функций
![]()
Положим
![]() и т.д. Эти функции связаны между собой
следующими рекурсивными соотношениями:
и т.д. Эти функции связаны между собой
следующими рекурсивными соотношениями:
![]()
Продолжим эту последовательность, положив, по определению

![]()
Эта схема имеет вид примитивной рекурсии,
следовательно, все функции
![]() примитивно рекурсивные. Растут они
крайне быстро, например,
примитивно рекурсивные. Растут они
крайне быстро, например,
![]()
![]()
Зафиксируем теперь значение
![]() .
Получим последовательность одинаковых
одноместных функций
.
Получим последовательность одинаковых
одноместных функций![]() .
Определим теперь функцию
.
Определим теперь функцию![]() ,
которая перечисляет эту последовательность:
,
которая перечисляет эту последовательность:![]() ,
то есть
,
то есть![]()
![]() и так далее, а так же диагональную функцию
и так далее, а так же диагональную функцию![]() .
.
Эти функции
![]() называются функциями Аккермана.
называются функциями Аккермана.
Из соотношений
![]() следует, что
следует, что

![]()
Эти соотношения позволяют вычислять
значения функций
![]() и, следовательно,
и, следовательно,![]() ,
причем для вычисления функций в
данной точке, нужно обратится к
значению функции в предшествующей точке
- совсем как в схеме примитивной рекурсии.
Однако здесь рекурсия ведется сразу по
двум переменным (также рекурсия
называется двойной, двукратной или
рекурсией 2-й ступени) и это существенно
усложняет характер упорядочения точек,
а, следовательно, и понятие предшествования
точек также усложняется. Например,
,
причем для вычисления функций в
данной точке, нужно обратится к
значению функции в предшествующей точке
- совсем как в схеме примитивной рекурсии.
Однако здесь рекурсия ведется сразу по
двум переменным (также рекурсия
называется двойной, двукратной или
рекурсией 2-й ступени) и это существенно
усложняет характер упорядочения точек,
а, следовательно, и понятие предшествования
точек также усложняется. Например,![]() ,
а так как
,
а так как![]() ,
то вычислению
,
то вычислению![]() в точке
в точке![]() по схеме
по схеме![]() должно предшествовать вычисление
должно предшествовать вычисление![]() в точке
в точке![]() .
Вычислению
.
Вычислению![]() в точке
в точке![]() должно предшествовать вычисление в
точке
должно предшествовать вычисление в
точке![]() .
Важно отметить, что это предшествование
не определено заранее, как в схеме
примитивной рекурсии, где
.
Важно отметить, что это предшествование
не определено заранее, как в схеме
примитивной рекурсии, где![]() всегда предшествует
всегда предшествует![]() ,
а вычисляется в ходе вычислений и для
исходной схемы вида
,
а вычисляется в ходе вычислений и для
исходной схемы вида![]() вообще говоря различно. Поэтому схему
двойной рекурсии (в отличии от
рассматриваемой ранее одномерной
рекурсии) не всегда удается свести к
схеме примитивной рекурсии.
вообще говоря различно. Поэтому схему
двойной рекурсии (в отличии от
рассматриваемой ранее одномерной
рекурсии) не всегда удается свести к
схеме примитивной рекурсии.
Теорема 2. Функция Аккермана![]() растет быстрее, чем любая примитивно
рекурсивная функция и, следовательно,
не является примитивно рекурсивной.
Более того, для любой одноместной
примитивно рекурсивной функции -
растет быстрее, чем любая примитивно
рекурсивная функция и, следовательно,
не является примитивно рекурсивной.
Более того, для любой одноместной
примитивно рекурсивной функции -![]() ,
найдется такое
,
найдется такое![]() ,
что для любого
,
что для любого![]()
![]() .
.
Ограничимся наброском доказательства, опустив некоторые выкладки.
Вначале доказываются два свойства функции
 :
:
![]()
![]()
![]()
![]()
Назовем функцию

 - мажорируемой, если существует
натуральное
- мажорируемой, если существует
натуральное такое, что для любых
такое, что для любых ,
удовлетворяющих условию
,
удовлетворяющих условию
![]()
Покажем, что все примитивно рекурсивные
функции
![]() -
мажорируемы:
-
мажорируемы:
для простейших функций
 их
их - мажорируемость очевидна;
- мажорируемость очевидна;рассмотрим оператор суперпозиции, причем для простоты выкладок ограничимся функцией
 .
.
Пусть функции
![]() - мажорируемы с числами
- мажорируемы с числами![]() соответственно. Положим
соответственно. Положим![]() .
Тогда по определению
.
Тогда по определению![]() -
мажоририуемости и свойствам
-
мажоририуемости и свойствам![]() ,
,![]() :
:

и, следовательно, с учетом
![]() и
и![]()
![]()
т.е.
![]()
![]() - мажорируема;
- мажорируема;
рассмотрим теперь оператор примитивной рекурсии, ограничившись для простоты схемой:
![]()
Пусть
![]()
![]() - мажорируема, т.е.
- мажорируема, т.е.![]() при
при![]() .
Докажем индукцией по
.
Докажем индукцией по![]() ,
что
,
что![]()
![]() - мажорируема.
- мажорируема.
Учитывая условие в определении
![]() - мажорируемости, индукцию надо начинать
с
- мажорируемости, индукцию надо начинать
с![]() .
Пусть
.
Пусть![]() .
.
Из
![]() ,
,![]() следует,
что
следует,
что![]() ,
поэтому найдется такая величина
,
поэтому найдется такая величина![]() ,
что
,
что![]() .
.
Положим
![]() .
Очевидно, что
.
Очевидно, что![]() .
.
П![]() усть
теперь
усть
теперь![]() .
.
Тогда
![]() .
.
Если
![]() ,
то используя
,
то используя![]() -
-![]() и то, что
и то, что![]() ,
имеем
,
имеем
![]()
![]()
Если же
![]() ,
то в силу
,
то в силу![]() -
-![]()
![]() ,
что и завершит индукцию.
,
что и завершит индукцию.
Из п. (а), (б) и (в) следует, что все примитивно
рекурсивные функции
![]() - мажорируемы.
- мажорируемы.
Пусть
 - примитивно рекурсивная функция. В
силу п. 2 для некоторого
- примитивно рекурсивная функция. В
силу п. 2 для некоторого и
и
 .
Но тогда
.
Но тогда ,
то есть
,
то есть ,
начиная, по крайней мере, с
,
начиная, по крайней мере, с .
.
