§3. Доказательство основной теоремы.

Основная теорема гласит: каждый LJ-вывод (соответственно LJ-вывод) можно преобразовать в LJ-вывод (соответственно в LK-вывод) с той же секвенцией, в который не входит сечение.

3.1. Доказательство основной теоремой для LK-вывода. Мы вводим (для объяснения доказательства) некоторую новую фигуру заключения, которая представляет собой видоизменения сечения; мы называем её «смещением».

Схема её такова:

Здесь  и  замещается рядом формул, отделённых друг от друга запятыми, в которые вида M, называется «формулой смешения», входит по крайней мере один раз (в качестве члена ряда);

и замещается теми же рядами формул, из которых всюду исключена (как член ряда) формула видаM (M может быть любой формулой).

 и  должны, как обычно, замещаться произвольными (возможно, и пустыми) рядами формул, отделённых друг от друга запятыми.

Пример смещения:

Формулой смешения является В.

Очевидно, каждое смещение можно преобразовать в смещение с утончениями и перестановками (можно и обратно: каждое смещение преобразовать в сечение с предшествующими перестановками и сокращениями; этим мы не пользуемся).

В дальнейшем мы рассматриваем лишь выводы, в которые не входят сечения, но могут входить смешения.

Далее достаточно доказать следующую лемму.

Лемма. Всякий вывод, содержащий смешение в качестве самой нижней фигуры заключения и не содержащий других смешений, можно преобразовать в вывод (с той же секвенцией), в который смешение не входит.

Отсюда можно вывести основную теорему следующим образом. В произвольном выводе рассматривается смешение, выше нижней секции у которого нет других смешений. Вывод этой нижней секции имеет вид, отмеченный в условии леммы, следовательно, его можно преобразовать в вывод без смешений. При этом вся основная часть этого вывода не изменяется. Даже повторяется то же самое, пока не будут устранены все смешения.

Теперь нам остаётся лишь провести доказательство леммы (оно продолжится до 3.2).

Мы рассмотрим вывод, содержащий смещение в качестве самой нижней фигуры заключения и не содержащий других смещений.

«Степенью вывода» мы назовём степень формулы смещения (определения в I , 2.2).

«Рангом вывода» мы назовём сумму первого и иного ранговых чисел, корни мы определим так:

Левое ранговое число есть наибольшее число секвенций, содержащих формулу смещения сукцеденте и идущих в конце одной нити непосредственно друг за другом, причём нижняя из них является левой верхней секвенцией смещения.

Первое ранговое число есть (соответственно) наибольшее число секвенций, антецеденте и идущих в конце одной нити непосредственно друг за другом, причём нижняя из них является первой верхней секвенцией смешения.

Очевидно, ранг не может быть меньше 2.

Для доказательства леммы мы проводим две полные индукции, по степени вывода γ и по рангу вывода ρ.

Мы доказываем теорему для вывода степени γ, предполагая при этом, что она верна для выводов меньших степеней (если существует, т.е. если γ  0 ), т.е. что такие выводы можно преобразовать в выводы без смещения.

Далее мы рассматриваем случай когда ранг вывода ρ=2 (3.11), а за тем случай когда ρ>2 (3.2), причём мы предполагаем, что для выводов той же степени, но меньшего ранга, теорема верна.

(Т.е., при доказательстве основной теоремы автор пользуется по 3 параметрам: по числу смещений в выводе, степени вывода и размеру вывода).

В дальнейшем, как и до сих пор, прописные готические буквы будут служить для обозначения формул, прописные буквы для обозначения рядов формул (возможно, и пустых).

При преобразовании вывода будут иногда появляться «тождественные фигуры заключения», т.е. фигуры заключения с одинаковыми верхними и нижними секвенциями. Так как мы не допускаем таких фигур в нашем исчислении, их нужно каждый раз устранять тривиальным образом: просто опускается одна из двух тождественных секвенций.

Форму смешения, стоящую в конце вывода, мы обозначим по средствам M. Она имеет степень γ.

3.10. Переименование свободных предметных переменных, как подготовка к преобразованию вывода.

Мы хотим добиться, чтобы вывод обладал следующим свойством:

3.10.1. Для каждой ASL (соответственно EEA) имеет место следующее:

её собственная переменная встречается в выводе только в секвенциях, стоящих выше каждой секвенции AES (соответственно EEA) и не выходит не в какую другую AES или EEA в каждой её собственной переменной.

3.10.2. Это достигается в результате следующего переименования свободных предметных переменных:

выделим такую AES (соответственно EEA), выше нижней секвенции у которой нет фигур заключения одного из этик видов, кроме тех, которых данное преобразование уже проведено.

Собственную переменную видимой фигуры заключения заменяем во всех секвенциях, стоящих выше ее нижней секвенции, одной и той же свободной предметной переменной не встречавшейся ранее в выводе. Как легко проверить, AES (соответственно, ЕЕА) остается при этом корректной фигурой заключения того же вида (собственная переменная не входит в ее нижнюю секвенцию). Остальной вывод также остается выводом, что следует из приведенного ниже вспомогательного утверждения.

Проделав описанное преобразование последовательно к каждой отдельной AES и EEA, мы снова получим вывод, но уже обладающий свойством 3.10.1. При этом существенно, что степень и ранг вывода, а также его конечная секвенция, остаётся без изменения.

3.10.3. Мы проведем теперь доказательство следующего вспомогательного утверждения.

«Каждая основная секвенция и фигура заключения исчисления LK переходит в основную секвенцию или в фигуру заключения того же вида, когда мы заменяем некоторую входящую в неё свободную предметную переменную, не являющейся её собственной переменной, всюду, где она входит в неё, одной и той же свободной предметной переменной, которая также не является собственной переменной данной фигуры заключения.»

Это утверждение тривиально для всех фигур заключения, кроме AES, AEA, EES и EEA.

Но даже в этих случаях всё в порядке: ограничения на переменные не нарушается, так как мы не вводим новых собственных переменных. (По этой причине оба условия являются необходимыми). Далее формула возникающая из FA, переходит при замене а на x в формулу возникающую из Fx .

После подготовительного шага 3.10 следует уже основное преобразование вывода, имеющее целью входящего в него смещения.

Как было сказано мы рассмотрим два случая: ρ =2 (3.11) и ρ> 2 (3.12).

3.11. Пусть ρ=2.

Мы рассмотрим несколько отдельных случаев. При этом случаи 3.11.1, 3.11.2, 3.11.3.1, 3.11.3.2 особенно просты; в этих случаях смещение совсем удаляется. Остальные случаи 3.11.3.3 более сложны, при их рассмотрении находит выражение основная идея всего преобразования. Здесь мы используем индукционное предположение относительно γ, то есть в каждом из этих случаев сводим построение вывода без смещения к построению такого вывода меньшей степени.

3.11.1. Левая верхняя секвенция смещения, стоящего в конце вывода, является основной секвенцией. Тогда смещение имеет вид:

M → M ∆ → Λ

M, ∆^* → Λ

Оно преобразуется так:

Δ → Λ

возможно несколько перестановок и сокращений.

M, Δ →Λ

Часть вывода выше Δ→Λ остаётся без изменения мы получаем вывод уже без смещений.

3.11.2. Правая верхняя секвенция смещения является основной секвенцией. Этот случай рассматривается симметрично предыдущему рассмотрение одного из них должно быть «зеркальным отражением» рассмотрения другого (ср 2.4).

3.11.3. Ни левая, ни правая из верхних секвенций смещения не является основной секвенцией. Тогда обе они являются нижними секвенциями фигур заключения. Так как ρ=2 , то и правое и левое ранговые числа равны 1, то есть m не входит в сукцедент секвенции, стоящей непосредственно над левой верхней секвенцией смещения, а так же антецедент секвенции, стоящей непосредственно над правой верхней секвенцией смещения.

Вообще имеет место следующее: если формула входит в антецедент (соответственно в сукцедент) нижней секвенции фигур заключения, то она является главной фигурой последней, или определения уточнения, или входит антецедент (соответственно в сукцедент) по крайней мере одной из верхних секвенций этой фигуры заключения.

Это можно установить непосредственно из схем фигур заключения (1.21, 1.22).

Рассмотрим теперь следующие 3 случая, которыми, как легко видеть, исчерпываются в совокупности все возможные случаи, описанные в 3.11.3.

3.11.3.1. Левая верхняя секвенция смешения является нижней секвенцией утончения. Конец вывода имеет вид:

Г → Θ

Г→Θ, MΔ→ Λ

Г, Δ^* → Θ , Λ

Он преобразуется в:

Г → Θ

возможно несколько утончений и перестановок

Г, Δ^* → Θ , Λ

Часть вывода выше Δ → Λ отбрасывается совсем .

3.11.3.2. Правая верхняя секвенция смешения является нижней секвенцией уточнения. Этот случай рассматривается симметрично предыдущему.

3.11.3.3 Формула смешения M входит в сукцедент левой и антецедент правой верхних секвенций смешения только в качестве главной формулы любой из логических фигур заключения.

В соответствии с тем, что по числу внешних знаков M может быть &, , , ,  или  (формула без множественных знаков не может быть главной формулой), надо рассматривать шесть случаев: от 3.11.3.3.1 до 3.11.3.3.6.

3.11.3.3.1. Внешний знак M есть &. Тогда конец вывода имеет вид:

Г

UES

UEA

₁ → Θ₁, U Г₁→ Θ₁ Г₂→ Θ₂

смешение

Г₁→ Θ₁, U & B U & B, Г₂→ Θ₂

Г₁,Г₂→ Θ₁, Θ₂

(рассмотрение этого случая для другой формулы UEA совершенно аналогично). Он преобразуется в:

Г

смешение

₁ → Θ₁, U U, Г₂→ Θ₂

Г₁, Г₂^* → Θ₁^*, Θ₂

возможно, несколько уточнений и перестановок

Г₁,Г₂→ Θ₁, Θ₂

(при этом часть вывода, стоящая, над правой верхней секвенцией UEA, и сама эта секвенция удаляются из вывода).

К той части вывода, самой нижней секвенции которой является Г₁,Г₂^*→ Θ₁^*, Θ₂ , принимать индукционное предположение γ , так как она имеет степень, чем γ (U содержит менее логических знаков, чем в U&B). Итак, весь вывод можно преобразовать в вывод, не содержащий смещений.

3.11.3.3.2. Внешний знак M есть V этот случай рассматривается симметрично предыдущему.

3.11.3.3.3. Внешний знак M есть . Тогда конец вывода имеет вид:

Г

AES

AEA

₁ → Θ₁, Fa Fb, Г₂→ Θ₂

Г

смешение

₁→ Θ₁, xFx xFx, Г₂→ Θ₂

Г₁,Г₂→ Θ₁, Θ₂

Он преобразуется в

Г

смешение

₁ → Θ₁, Fb Fb, Г₂→ Θ₂

Г₁,Г₂^* → Θ₁^*, Θ₂

возможно, несколько уточнений и перестановок

Г₁,Г₂→ Θ₁, Θ₂

Над левой верхней секвенцией смещения Г₁→ Θ₁, Fb пишется такая же часть вывода, какая раньше стояла над Г₁→ Θ₁, Fa, но в ней всюду свободная предметная переменная a заменяется на b. Из вспомогательного утверждения 3.103 и из 3101 следует, что полученная таким образом над Г₁→ Θ₁, Fb часть вывода является правильной частью вывода. Такое рассуждение можно применять к части вывода до секвенции Г₁→ Θ_1, Fb включительно, так как также является результатом подстановки b вместо a в Г₁→ Θ₁, Fa.

Действительно, в силу ограничения на переменные для AES, а не может входить в Г₁, Θ₁ или в Fx. Следовательно, Fa в результате замены x в Fx на а, Fb в результате замены x в Fx на b. Поэтому и Fb в результате замены а в Fa на b.

Формула смещения M имеет в новом виде степень, меньшую чем γ, так что по индивидуальному положению смещения можно устранить.

3.11.3.3.4. Знак M есть . Этот случай рассматривается симметрично предыдущему.

3.11.3.3.5. Знак M есть ⌐. Конец вывода имеет вид :

NES

NEA

U, Г₁→ Θ₁ Г₂→ Θ₂, U

смешение

Г₁→ Θ_1, ⌐U ⌐U, Г₂→ Θ₂

Г₁, Г₂→ Θ₁, Θ₂

Он преобразуется в:

Г

смешение

₂ → Θ₂, U U, Г₁→ Θ₁

Г₂, Г₁^* → Θ₂^*, Θ₁

возможно, несколько уточнений и перестановок

Г₁, Г₂→ Θ₁, Θ₂

Новое смешение можно устранить по индукционному предположению.

3.11.3.3.6. Внешний знак M есть . Конец вывода имеет вид

U

FES

FEA

, Г₂→ Θ₁, B Г→ Θ, U B, 

Г

смешение

₁→ Θ₁, UB UB, Г, Θ, 

Г₁, Г_, →Θ₁, Θ, 

Он преобразуется в

смешение

U, Г₁→ Θ₁, B B, 

Г

смешение

→ Θ,U U, Г₁, ^* → Θ₁^*, 

Г, Г₁^* ^**→ Θ^*, Θ₁^*, 

возможно, несколько уточнений и перестановок

Г₁,Г, → Θ₁, Θ, 

(Звёздочки соответственно, означают, что Δ* и Θ ₁* получается из Δ и Θ в результате удаления всех S-формул вида B; Г₁*, Δ** и Θ * получается из Г,Δ*, Θ в результате удаления всех S-формул вида U).

Мы ищем в этом случае два смещения, но в каждом из них формула смещения имеет степень, меньшую, чем . Применяем индукционное предположение сначала к верхнему смещению (т.е. к той части вывода, для которой это смещение является частью нижней фигуры заключения). Оно устраняется после этого мы можем также устранить нижние смещения.

3.12. Пусть ρ>2.

Мы различаем теперь два главных случая:

1) правое ранговое число больше 1 (3.12.1).

2) правое ранговое число равно 1 и поэтому левое ранговое число больше 1 (3.12.2).

Второй случай по существу, может рассматривать симметрично первому.

3.12.1. Правое ранговое число больше 1.

Это значит, что правая верхняя секвенция смещения является нижней секвенция некоторой фигуры заключения, которую мы обозначим посредством f и формула M входит по крайней мере одной из верхних секвенций f.

Основная идея преобразования следующая:

eсли в случае, когда ρ=2, мы вообще говоря, сводим задачу к преобразованию вывода низшей степени, то теперь мы будем сводить задачу к преобразованию вывода той же степени, но меньшего ранга, так что мы можем применить индукционное предположение относительно ρ.

Исключения составляет лишь первый из рассматриваемых случаев: здесь возможно сразу совсем исключить смещение (3.12.1.1).

В остальных случаях сведение к выводу с меньшим рангом достигается следующим образом:

Смешение перемещается вверх на одну ступень фигурой заключения f точнее говоря (как особенно нещадный пример, можно рассмотреть случай 3.12.1.2.3.1), левая верхняя секвенция смещения (в дальнейшем всюду записываем в виде П→Σ), стоящая сначала рядом с нижней секвенцией f, после преобразования оказывается написанной рядом с верхней секвенцией f, которая служит верхней секвенцией нового смещения. А нижняя секвенция этого нового смещения служит тогда верхней секвенцией новой фигуры заключения, появится на месте f, с помощью которой и, быть может, с использованным ещё новых фигур заключения, мы получаем старую конечную секвенцию.

Новое смещение, очевидно, имеет ранг, меньший чем ρ, т.к. левое ранговое число не изменяется, а главное уменьшается по крайней мере на 1.

При точном проведении в жизнь этой основной идеи встречаются различные особенности, требующие соответствующего деления на подслучаи и особого рассмотрения каждого из них.

3.12.1.1. M входит в антeцедент левой верхней секвенции смещения. Конец вывода имеет вид:

П

cмещение, M входит в П

→Σ Δ→Λ

П, Δ*→Σ*, Λ

Преобразуем его так:

возможно, несколько уточнений, перестановок и сокращений

Δ→ Λ

П, Δ*→Σ*, Λ

3.12.1.2. M не входит в антецедент левой верхней секвенцией смещения. (Это условное впервые будет использовано в 3.12.1.2.2.2).

3.12.1.2.1. Пусть f-уточнение, сокращения или перестановка в антецеденте. Тогда конец вывода имеет вид

П

cмешение

→Σ

П, Δ*→Σ*, Λ

Преобразуем его так:

П

cмешение

→Σ→

П, Δ*→Σ*, 

возможно, несколько перестановок,

см. ниже,

*, П→Σ*, 

*, П → Σ ^*, Θ

возможно, несколько уточнений и перестановок

П, *→Σ*, 

Если S-формулы, обозначенные в схеме f посредством D и C (см 1.21), не совпадает с M, то фигура заключения, название которой в написанной выше части вывода не указано, имеет ниже вид что и f. Если D и C совпадает с M, то не названная фигура является тождественной фигурой заключения (ψ* совпадает с Ξ*).

Вывод нижний секвенции нового смешения имеет то же самое левое ранговое число, что и старый вывод, а его первое ранговое число на 1 меньше, т.е. по индуктивному предположению смешение может быть устранено.

3.12.1.2.2. Пусть f-фигура заключённая с явной верхней секвенции, но не уточнение, сокращения или перестановка в антецеденте:

Конец вывода имеет вид

П

cмешение

→Σ

П, Ξ*, Г*→Σ*, Ω₂

При этом посредством Г обозначает те же S-формулы, которые в схеме соответствующие фигуры заключения обозначены по средствам Г(1.2.1, 1.2.2).  или пусто или состоит из одной боковой формулы фигуры заключения Ξ или пусто или состоит из левой формулы фигуры заключения.

Преобразуем сначала этот конец выводе так:

П

возможно, несколько перестановок и уточнений

cмешение

→ Σ Ψ , Г → Ω₂

П, Ψ ^*, Г ^*→ Σ*, Ω₂

Ψ, Г^*, П→ Σ*, Ω₁

Ξ,Г^*, П→ Σ*, Ω₂

Самая нижняя фигура заключения является, конечно, фигурой того же вида, что и f (считая, что Г*, П совпадает с Г данной фигуры заключения Σ* совпадает с  этой фигуры).

Оно остаётся выполненным, т.к в силу 3.10.1 собственная переменная фигуры f не может входить ни в П, ни в Σ.

Из нового вывода смещения устраняется по индукционному предположению.

Мы получим после этого вывод без смещения последняя фигура заключения имеет вид:

Ψ, Г^*, П→ Σ*, Ω₁

Ξ, Г^*, П→ Σ*, Ω₂

Каждая секвенция здесь, вообще говоря, отличается от той, которую надо было получить.

Далее поступим следующим образом.

3.12.1.2.2.1. Ξ не содержит M.

В этом случае применив по мере необходимости несколько перестановок, можно получить конечную секвенцию исходного вывода.

3.12.1.2.2.2. Ξ не содержит M.

Тогда Ξ является главной формулой f и совпадает M. В этом случае присоединяем к выводу следующее:

П

смещение

→ ΣМ , Г^*, П→ Σ*, Ω₂

П, Г ^*, П^*→ Σ*, Σ*, Ω₂

возможно, несколько уточнений и перестановок

П, Г^*→ Σ*, Ω₂

Здесь уже получена конечная секвенция первоначального вывода.

(Над П → Σ пишется еще раз весь ее вывод.)

Однако в выводе имеется смешение. Его левое ранговое число то же, что в первоначальном выводе. Правое ранговое число равно 1, так как непосредственно над правой верхней секвенцией стоит секвенция

Ψ, Г^*, П→ Σ*, Ω₁,

в антецедент которой M уже не входит.

Действительно, Г^* не не содержит M, П – также, по 3.12.1.2 и Ψ содержит самое большое одну боковую формулу f, которая не может быть формулой M, так как главная формула f совпадает с M.

Таким образом, и это смещение можно устранить по индивидуальному предположению.

3.12.1.2.3. Пусть f – фигура заключения с двумя верхними секвенциями, т.е. UES, OEA или FEA.

Принимая во внимание интуиционистское примечание (3.2), мы рассмотрим каждую из этих возможностей подробнее, чем это необходимо в классическом случае.

3.12.1.2.3.1. Пусть f есть UES. Тогда конец имеет вид:

П

cмешение

→Σ

П , Г^*→ Σ*, ,U&B

(M входит в Г). Он преобразуется следующим способом:

Оба смещения можно удалить по индукционному предположению.

3.12.1.2.3.2. Пусть f есть OEA. Тогда конец вывода имеет вид:

П

cмешение

→Σ

П, (UB)^*, Г^* → Σ*, Θ

((UB)^* или обозначает формулу UB или пусто в зависимости от того, отлично UB от M или совпадает с M ) .

M непременно входит в Г (ибо в противном случае M совпадает с UB и правое ранговое число будет равно 1, что противоречит 3.12.1).

Конец вывода сначала преобразуется в

OEA

смешение

возможно, несколько перестановок и уточнений

UB, П, Г^*→ Σ*,

Оба смещения можно удалить по индукционному предложению.

После этого надо поступить так же, как и в 3.12.1.2.2.1 и 3.12.1.2.2.2. Следовательно, мы рассмотрели два случая, в зависимости от того, отлично UB то M или совпадает с M ;

В первом случае мы добавляем по мере надобности несколько перестановок и получим таким образом конечную секвенцию первоначального вывода;

Во втором случае мы присоединим смещение с Пв качестве левой секвенции и, сделав, если необходимо, несколько дополнительных сокращений и перестановок, также получим конечную секвенцию первоначального вывода. Новое смещение можно устроить, так как соответствующее ему ранговое число равно 1.

3.121.233. f есть FEA. Тогда конец вывода имеет вид:

П

cмешение

→Σ

П , (UB) ^*, Г^*, Δ^*→ Σ*, ,Λ

3.12.1.2.3.3.1. M входит в Г и Δ. Тогда конец вывода сначала преобразуется в:

смешение

возможно несколько перестановок и уточнений

FEA

cмешение

UB, П, Г^*, П, Δ^*→ Σ*, , Σ*, Λ

Оба смешения устранимы по индукционному предположению. После этого поступают так же, как в 3.12.1.2.2.1 и 3.12.1.2.2.2. (Возможно лишь, что в этом случае, кроме перестановок, потребуется сделать еще сокращения.)

3.12.1.2.3.3.2. M не входит одновременно в Г и в Δ. В одном из этих рядов M непременно входит в силу 3.121. Мы рассмотрели случай, когда М входит в Δ и не входит в Г; другой случай рассматривается аналогично.

Конец вывода преобразуется в

смешение

Г→ ,U

FEA

возможно несколько перестановок и уточнений

UB, Г, П, Δ^*→ Σ*, , Σ*, Λ

Смешение можно устранить по индукционному предположению.

После этого поступают так же, как и в 3.12.1.2.2.1 и 3.12.1.2.2.2 (во втором случае, то есть когда UB совпадает с M, правое ранговое число нового смещения, как и всегда, равно 1, так как M не входит в B, П, Δ^* На том же основании, что и ранее, а в Г согласно условию рассмотренного случая).

3.12.2. Пусть правое ранговое число равно 1. Тогда левое ранговое число меньше 1.

Это случай можно рассмотреть зеркально – симметрично случаю 3.12.1. Надо обратить внимание лишь на фигуры заключения, не имеющие симметричных, так как на FES и FEA. Все фигуры заключения f, рассмотренные в 3.12.1.2.2, т.е имеющие одну верхнюю секвенцию, мы включим в одну общую схему:

Ψ, Г → Ω₁

Ξ, Г→Ω₂

Зеркально-симметричная схема будет такова :

Ω₁→ Г, Ψ

Ω₂→ Г, Ξ

А она включает в себя и FES.

(Г представили здесь формулы, обозначенные в схемах 1.2.1, 1.2.2 посредствам .)

3.12.2.1. Напротив, случай, когда фигура заключения f есть FEA, мы хотим рассмотреть особо. Хотя способ, который мы применяли, очень сходен со способом, измененным в 3.12.1.2.3.3, он не вполне зеркально-симметричен ему.

Конец вывода имеет вид:

Г

FEA

→,U B, Δ→Λ

смешение

UB, Г, Δ→Θ, Λ → П

UB, Г, Δ, Σ* →Θ^*, Λ^*, П

3.12.2.1.1. М входит в Λ и в Θ. Тогда конец вывода преобразуется

смешение

FEA

смешение

возможно несколько перестановок и уточнений

возможно несколько перестановок и уточнений

Оба смешения можно устранить по индукционному предположению.

3.12.2.1.2. М не входит в  и в Λ одновременно. В одном из этих рядов m должно входить. Мы рассмотрим случай, когда m входит в Λ и не входит в , другой случай рассматривается аналогично.

Конец вывода преобразуется в

Г→ ,U

смешение

FEA

UB, Г, Δ, Σ* →Θ^*, Λ^*, П

Смешение можно устранить по индукционному предположению.

3.2. Доказательство основной теоремы для LJ–выводов.

Для преобразования LJ-вывода в LJ-вывод без сечения мы применяем точно такой же способ, как и для LK-выводов.

Т.к. ZJ-вывод является частным случаем LK-вывода, то ясно, что описанные преобразования могут быть выполнены.

Мы должны лишь убедиться в том, что при каждом шаге преобразования из LJ-вывода получается также LJ-вывод, т.е. что H-секвенции преобразованного вывода содержат в сукцеденте не более одной функции, если так было до преобразования.

3.2.1. Замена сечений смешениями.

LJ-сечение имеет вид: , где содержит не более одной формулы. Она преобразуется

возможно несколько перестановок и уточнений в антецеденте

смешение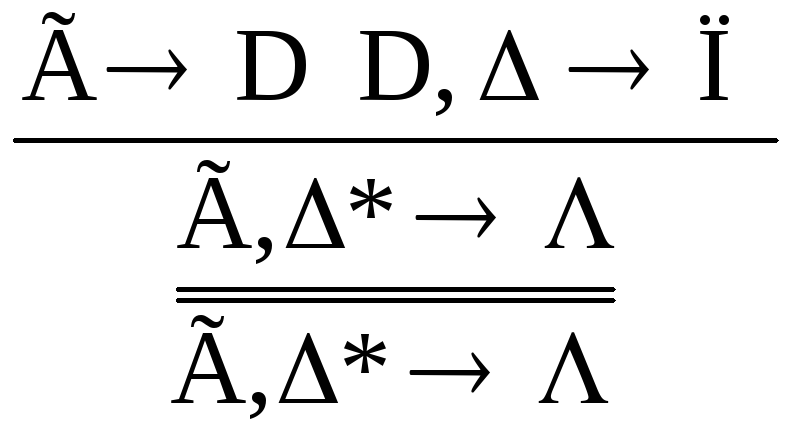

При такой замене получается, как видно, снова LJ-вывод.

3.2.2. При переименовании свободных предметных переменных (3.10) LJ-вывод, очевидно переходит в LJ-вывод.

3.2.3. Собственно преобразование (3.11 и 3.12). Мы должны убедиться в том, что в каждом отдельном случае, начиная с 3.11.1 и до 3.12.2.1.2, в результате осуществленного там преобразования ни появляется ни одной секвенции, содержащей более одной формулы в сукцеденте?

3.2.3.1. Сначала случай п. 3.11.

В случаях 3.11.1, 3.11.3.1, 3.11.3.3.1, 3.11.3.3.5 и 3.11.3.3.6 в сукцедент каждой секвенции нового вывода входят лишь формулы, входящие в сукцедент некоторой секвенции старого вывода.

В случае 3.11.3.3.3, по существу, имеет место то же самое, но здесь добавляется еще замена свободных предметных переменных, что не изменяет числа формул в сукцеденте секвенции.

Случаи 3.11.2, 3.11.3.2, 3.11.3.3.2 и 3.11.3.3.4 можно рассмотреть симметрично случаи 3.11.1, 3.11.3.1, 3.11.3.3.1 и 3.11.3.3.3. Симметрично, чтобы получить один из другого, надо прочитать схемы не слева направо, а наоборот (справа налево и также заменить логические знаки, что здесь не играет роли). Таким образом, в одном из этих случаев в антецеденте стоит в точности то же самое, что для сукцедентов, а именно: в антецедент каждой секвенции нового вывода входят лишь те формулы, которые уже входили в антецедент некоторой секвенции старого вывода.

Этим исчерпаны зеркально-симметричные случаи 3.11.2, 3.11.3.2, 3.11.3.3.2 и 3.11.3.3.4.

3.23.2 Теперь случай пункта 3.12.

3.23.2.1. В случаях 3.121 вообще ∑* является пустым, т.к. в секвенции П→∑ список ∑ может содержать только одну формулу, которая должна быть формулой M.

Теперь легко видеть, что и здесь в суквенции каждой секвенции нового вывода входят только те формулы. Которые уже входили в сукцедент некоторой секвенции старого вывода.

3.23.2.2 В случае 3.12.2 не очевидно, что из LJ-вывода получается LJ-вывод. Надо обратить внимание на антецеденты в схемах 3.12.1. Рассмотрим следующие случаи.

3.23.2.2.1 Случай, зеркально-симметричный 3.12.1.1, тривиален, т.к. в антецедент каждой секвенции нового вывода (в 3.12.1.1) входя лишь формулы. Входившие в антецедент некоторой секвенции старого вывода.

3.23.2.2.2 В случаях, зеркально-симметричных 3.12.1.2, смешение в конце вывода имеет вид

где П состоит не более чем из одной S-формулы и Ω→M есть частная секвенция некоторой LJ-фигуры заключения, по крайней мере одна из верхних секвенций которой служит M в сукцеденте.

Если мы рассмотрим теперь схемы фигур заключения 1.2.1, 1.2.2, то легко заметить, что такой фигурой заключения может быть только умножение, сокращение или приставка в антецеденте или одна из фигур: OEA, UEA, EEA, AEA, FEA. Оставим пока в стороне OEA и FEA; видим, что все остальные из перечисленных фигур заключения являются зеркально-симметричными 3.12.1.2.2 и, как очевидно, Ψ и Ξ при этом всегда пусты. (Г соответствует в фигурах заключения Θ). То есть мы имеем случай, зеркально-симметричный 3.12.1.2.2.1. Далее, если Г совпадает с M, то Г* пусто и П состоит не более, чем из одной формулы.

Следовательно, в новом выводе в сукцедент каждой секвенции действительно входит не более одной формулы.

Случай OEA является зеркально-симметричным случаю 3.12.2.1.2.3.1. Снова, если Г совпадает с M, то Г* пусто и П содержит самое большее одну формулу, так что все в порядке.

Останется еще случай FEA, т.е. 3.12.2.1.

Для исчисления LJ список Θ из этой схемы пуст. (1.22). Поэтому может иметь место лишь случай, рассмотренный в 3.12.2.1.2. Λ* также пусто и П содержит не более одной формулы, так что и здесь из LJ-вывода получаем снова LJ-вывод.