5.6. Очередь

Очередь — частный случай линейного односвязного списка, для которого разрешены только два действия: добавление элемента в конец (хвост) очереди - Push и удаление элемента из начала (головы) очереди – Pop (рис. 5.3).

Как и стек структура «очередь» (QUEUE) широко используется в алгоритмах многих вычислительных процессов. Один из возможных вариантов модуля работы с очередью приведен ниже.

UNIT QUEUE;

Interface

Type u = ^Uzl;

Uzl = Record

x, y :Integer; {информационные поля узла}

L :u; {ссылка на следующий узел }

End;

{ h1 – указатель на начало очереди, h2 – указатель на конец очереди }

Procedure PopQ ( Var h1 :u; Var a, b :Integer ); {исключить из очереди}

Procedure PushQ ( Var h1, h2 :u; a, b :Integer ); {включить в очередь }

Function EmptyQ ( h1 :u ) :Boolean; {очередь пуста}

Implementation

Procedure PopQ;

Var t :u;

Begin

With h1^ Do Begin a:=x; b:=y; End;

t := h1; h1 := h1^.L; Dispose(t);

End;

Procedure PushQ;

Var t :u;

Begin New(t);

With t^ Do Begin L := Nil; x:=a; y:=b; End;

If EmptyQ( h1 ) Then Begin h1 := t; h2 := t; End

Else Begin h2^.L := t; h2 := t; End;

End;

Function EmptyQ ( h1 :u )

Begin EmptyQ := (h1 = Nil); End;

End.

Рассмотрим пример практической задачи из области обработки и распознавания изображений графики, для решения которой может быть использована очередь. Выделение скелета (остова, каркаса, срединных осей) изображения представляет собой операцию утончения, цель которой состоит в том, чтобы попытаться свести связные об­ласти элементов изображения с заданным набором свойств к обла­стям меньших размеров. С помощью утончения область при­водится к минимальной ширине поперечного сечения. Построение скелета — это операция, с помощью которой область преобразуется в фигуру, напоминающую каркас. На рис.5.4. приведен пример, иллюстрирующий обработку объекта прямоугольной формы простым алгоритмом выделения скелета.

Чтобы выразить структурные соотно­шения сложных объектов в сцене, часто оказывается достаточным представление объектов в виде скелета, или остова. Ясно, что скелет большинства объектов, как правило, можно представить значительно эффектив­нее, чем сам объект. Один из подходов к получению скелета за­ключается в утончении объекта до тех пор, пока не будет получена цепочка элементов с минимальной связностью.

Известен [12] способ получения скелета, названный преобразованием к срединным осям, который для каж­дого заданного объекта дает однозначный результат. Интуитивное определение такого преобразования основывается на аналогии со «степным пожаром» или «распространением волны». Рассмотрим изображение на рис. 5.4 области прямоугольной формы и представим себе, что это участки земли, покрытые высохшей травой. Если бы огонь возник одновременно по всему периметру участков, то он распространялся бы к их центрам до тех пор, пока не сгорела бы вся трава. В случае круглой области огонь распространялся бы к центру круга, который представляет собой точку самогашения огня. Для прямоугольной области огонь распространялся бы с каждой стороны. По мере продвижения огня слева и сверху линии огня будут встречаться и пожар будет затухать. Геометрическое место точек самогашения огня образует линию самогашения. Точки или линии самогашения называются срединными осями или скелетом фигуры. Вообще скелет состоит из множества точек, которые находятся на одинаковом расстоянии от двух бли­жайших к ним точек на границе фигуры. Это расстояние называется расстоянием самогашения фигуры. Границу фигуры можно восста­новить по ее скелету и расстоянию самогашения. Эта граница есть огибающая окружностей с радиусом, равным расстоянию самогашения, с центрами в каждой точке скелета. Другой иллюстрацией метода выделения скелета в рамках данной модели является распространение некоторого волнообразного процесса от границ вовнутрь объекта. Тогда скелет можно рассматривать как линию встречи фронтов волн от различных участков границ объекта (рис. 5.4).

Решение поставленной задачи состоит из двух основных этапов:

1) выделение внешних границ объекта (контура);

2) выделение скелета объекта.

Точки контура объекта рассматриваются как точки начального положения фронта волны. В дальнейшем фронт волны будет распространяться вовнутрь объекта, при этом точки объекта, по которым проходит волна будут помечаться специальной меткой (цветом). Моделирование движения фронта волны происходит следующим образом. Для каждой точки фронта рассматриваются ее 4 соседние точки растра - справа, сверху, слева и снизу. Если соседняя точка принадлежит объекту и еще не помечена, то ее координаты (x,y) запоминается, фиксируя точку следующего положения фронта волны.

При анализе соседей данной точки фронта волны может оказаться, что все эти соседи уже имеют метку. Эта ситуация рассматривается как момент встречи волн от противоположных границ объекта, т.е. как точка скелета (или как точка "самогашения огня" в методе "степного пожара"). После специальной пометки данная точка выпадает из дальнейшего процесса движения волны. Алгоритм завершается после выделения всех точек скелета.

Для реализации алгоритма удобной структурой является очередь. Первоначально в нее помещаются координаты контура объекта. Далее, из начала очереди извлекается координаты очередной точки фронта волны, с помощью них анализируются соседние точки и координаты тех из них, которые не имеют меток, записываются в конец очереди. Сами точки, которые попадают в очередь приобретают метку. Таким образом, из очереди извлекаются точки (точнее их координаты) предыдущего положения фронта, а добавляются в очередь координаты точек следующего положения фронта волны. Процесс распространения волны завершается, когда очередь оказывается пустой.

В этом алгоритме вспомогательной процедурой является выделение контурных точек объекта. Выделение контура во многих задачах анализа изображений может иметь самостоятельное значение. В данном случае основным требованием является запись координат контурных точек в очередь в порядке последовательного обхода границ объекта, например по часовой или против часовой стрелки. Такое требование продиктовано особенностями рассматриваемого алгоритма выделения скелета и представления изображений на дискретном растре.

Предлагается следующий алгоритм обхода границ объекта.

1. Путем сканирования изображения находим первую контурную точку и ее координаты (xn,yn) становятся текущими.

2. Последовательно анализируем 4-х возможных соседей текущей точки и ищем среди них следующую контурную точку. Просмотр соседей начинаетя с направления d+1, где d - напрвление прихода в данную контурную точку. Соседями для данной точки c координатами (x,y) являются:

- точка (x-1,y) (d=0);

- точка (x,y-1) (d=1);

- точка (x+1,y) (d=2);

- точка (x,y+1) (d=3).

Координаты найденной контурной точки записываем в очередь и они становятся текущими.

3. Если координаты текущей контурной точки совпадают с (xn,yn), то обход границы объекта завершен, иначе переход к п.2.

Следует иметь в виду, что объект кроме внешнего может иметь и несколько внутренних контуров. Поэтому после обхода внешнего контура сканирование изображения продолжается со следующей после (xn,yn) точки. Обход внутренних контуров производится по описанному выше алгоритму.

Таким образом, для выделения скелета изображения понадобятся три процедуры:

1. процедура поиска первой точки очередного контура изображения,

2. процедура обхода контура с запоминанием координат его точек в очереди и

3. процедура моделирования движения волны и выделения скелетных точек.

Реализация этих процедур с комментариями приведена ниже.

Program Sceleton;

Uses CRT, Graph, QUEUE;

Const n = 200; { n×n - размеры изображения }

c0 = 0; { цвет фона }

c1 = 15; { цвет объекта }

c2 = 7; { цвет закраски объекта при движении волны }

c3 = 8; { цвет выделенного скелета }

z: Array[1..2, 0..3] Of Integer=((-1, 0, 1, 0), {∆x} { матрица смещений }

( 0,-1, 0, 1)); {∆y}

Var h1, h2 :u; { начало и конец очереди }

x, y, d :Integer; { рабочие переменные }

{$I GrInit}

Function Poisk (Var x, y, d :Integer) :Boolean; {Ф-я поиска нач. точки контура}

{ При вызове ф-ции x,y – координаты начала поиска.

Если точка контура найдена, ф-ция возвращает:

TRUE,

x,y – координаты точки контура,

d=0, если это точка внешнего контура;

d=1, если это точка внутреннего контура.

Иначе - FALSE. }

Var a, b, i :Integer;

Begin

Poisk := True;

For b := y To n-2 Do {Циклы

For a:=x To n-2 Do сканирования изображения }

If GetPixel (a, b) = c1 Then {Если найдена точка объекта,

For i := 0 To 1 Do то просматриваем пред. и посл. точки.

If GetPixel (a+z[1, 2*i], b+z[2, 2*i]) = c0 Если точка контура найдена,

Then Begin x := a; y := b; d := i; Exit; End; вывод рез-тов }

Poisk := False; { Больше новых контурных точек на изображении нет }

End;

Procedure Kontur ( xn, yn, d :Integer); {Прохождение контура фигуры}

Var x, y, a, b :Integer;

Begin

x := xn; y := yn; { Начинаем с точки (xn,yn) }

Repeat { Цикл прохождения контура фигуры}

Repeat { Цикл просмотра окрестности точки контура }

d := (d+1) Mod 4; {Вычисление направления на следующего соседа

a := x + z[1, d]; b := y + z[2, d]; и его координат }

Until GetPixel (a, b) < > c0; { Если это точка контура, то выход из цикла }

x := a; y := b; { Координаты конт. точки становятся текущими }

PushQ (h1, h2, a, b); { Занесение их в очередь }

PutPixel (x, y, c2); {Закраска конт. точки на изображении }

d := (d + 2) Mod 4; { Формир-е направления на поиск след. конт. точки }

Until (x = xn) And (y = yn); {При достижении нач. точки контура – выход }

End;

Procedure Scelet; { Выделение скелета }

Var i, a, b, p, x, y :Integer;

Begin

Repeat { Цикл распространения волны }

PopQ (h1, x, y); { Взяли текущ. точку фронта волны из очереди }

p := 0; { p - признак нахождения след. точки фронта волны }

For i:=0 To 3 Do Begin { Цикл просмотра 4-х соседей }

a := x + z[1, i]; b := y + z[2, i]; {Вычисление координат соседа}

If GetPixel (a, b) = c1 Then Begin {Если сосед не помечен,

PushQ (h1, h2, a, b); запись его координат в очередь,

PutPixel (a, b, c2); пометка и

p := 1; установка признака }

End;

End;

If p = 0 Then PutPixel (x, y, c3); { Закраска точки скелета на изображении }

Until EmptyQ ( h1 ); { Выход из цикла, если очередь пуста }

End;

Begin

GrInit; { Вывод

SetTextJustify(CenterText, CenterText); изображения

SetTextStyle(0,0,18); OutTextXY(100,100,'E'); на экран }

h1 := Nil; h2 := Nil; { Вначале очередь пуста }

x := 1; y := 1; {Уст-ка начальных координат поиска контурной. точки }

While Poisk (x, y, d) Do Kontur (x, y, d); { Выделение контура объекта }

Scelet; { Выделение скелета объекта }

ReadKey; CloseGraph;

End.

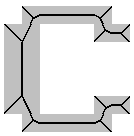
Рис. 5.5. Примеры выделения скелета для различных объектов.

На рис. 5.5 приведены результаты работы программы применительно к объектам различной формы.

Замечание. Применение на практике преобразования к срединным осям дискретных объектов, определенных на прямоугольном растре, связано с определенными трудностями. Чтобы обеспечить одно­значность преобразования, необходимо надлежащим образом ввести расстояние. Если объект имеет границу сложной формы, его скелет также будет сложным. С целью достижения более ком­пактного представления фигуры обычно проводится упрощение скелета объекта. Для многих объектов стира­ние или сглаживание частей скелета приводит к получению прибли­зительной границы объекта, которая не отличается заметно от истинной.

В следующем примере рассмотрим решение задачи из области машинной графики – закраски некоторой связной области заданным цветом. Постановка задачи была ранее сформулирована и приводился вариант ее решения с испрользованием рекурсии (см. п. 2.3 ). Сейчас приведем два варианта решения этой задачи: а) с использованием стека; б) с использованием очереди и сравним их с точки зрения их эффективности.

1 вариант закраски (разметки) связной области заданным цветом с использованием стека. Пусть задан стек, у которого каждый узел может хранить информацию о координатах x,y точки изображения, подобно приведенному ранее в модуле QUEUE. Модуль работы с таким стеком приведен ниже.