7.2. Построение остовного дерева минимального веса.

Среди всех каркасов графа в практическом плане часто интересует каркас минимального веса. Например, если граф является моделью для решения задачи проектирования сети связи между несколькими населенными пунктами – требуется минимизировать длину (стоимость) кабеля связи. В этом случае граф G = (V,E) будет связным взвешенным неориентированным, таким образом, каждому ребру приписано некоторое число (вес) (рис.7.4) и необходимо найти каркас с минимальным суммарным весом A = (V,B), где BE (рис.7.5).

Рассмотрим общую схему работы алгоритмов построения минимального остовного дерева с использованием жадной стратегии. Итак, пусть дан связный неориентированный граф G c n вершинами и весовая функция w: E → R.

Искомый остов строится постепенно. Алгоритм использует некоторый ациклический подграф А исходного графа G, который называется промежуточным остовным лесом. Изначально G состоит из n вершин-компонент, не соединенных друг с другом (n деревьев из одной вершины). На каждом шаге в A добавляется одно новое ребро. Граф A всегда является подграфом некоторого минимального остова. Очередное добавляемое ребро e=(u,v) выбирается так, чтобы не нарушить этого свойства: A U {e} тоже должно быть подграфом минимального. Такое ребро называется безопасным (ребро G называется безопасным (safe), если для некоторой компоненты A это ребро является самым лёгким из всех рёбер, соединяющих вершины этой компоненты с оставшимися вершинами).

Вот как выглядит общий алгоритм построения минимального остовного дерева:

MIN_OSTOV(G,w) 1: A ← 0 2: While (пока) A не является остовом 3:     Do найти безопасное ребро (u,v) ∈ E для A 4:          A ← A U {(u,v)} 5: Return A

По определению A, он должен оставаться подграфом некоторого минимального остова после любого числа итераций. Конечно, главный вопрос состоит в том, как искать безопасное ребро на шаге 3. Понятно, что такое ребро всегда существует, если A еще не является минимальным остовом (любое ребро остова, не входящее в A). Заметим, что так как A не может содержать циклов, то на каждом шаге ребром соединяются различные компоненты связности (изначально все вершины в отдельных компонентах, в конце A – одна компонента). Таким образом цикл выполняется (n-1) раз.

У задачи построения минимального остовного дерева длинная и богатая история[2 ]R. L. Graham and P. Hell. On the history of the minimum spanning tree problem. Annals of the History of Computing, 7(1): 43-57, 1985. Впервые работа на эту тему был опубликован в 1926 году Отакаром Борувкой в качестве метода нахождения оптимальной электрической сети в Моравии. В настоящее время наиболшую известность получили алгоритмы Крускала и Прима.

Алгоритм Крускала. Первый из предлагаемых алгоритмов принадлежи классу так называемых жадных алгоритмов. Этот алгоритм пытается найти решение поставленной задачи в лоб, стараясь найти минимальное остовное дерево последовательным отбором ребер с минимальным весом, следя за тем, чтобы получающийся граф не имел циклов. Разумеется, для этого необходимо сначала отсортировать все ребра графа по возрастанию их весов. Лучше всего, если граф с самого начала представлен списком ребер, в этом случае сортировка будет наиболее естественной. Но даже и в других случаях сортировка ребер графа по весу занимает не слишком много времени - в худшем случае mlog₂m, где m - количество ребер графа.

После сортировки ребер по весу строящееся остовное дерево организуется в виде отдельных фрагментов этого дерева, в которые в каждый момент времени включены все вершины графа. В начале работы каждая вершина графа представляет собой отдельную компоненту, а соединяющих их ребер пока вообще нет. Каждое вновь включаемое ребро соединяет две отдельные компоненты в одну, таким образом, полное остовное дерево будет построено после n-1 включения ребра. Разумеется, очередное ребро можно включить в дерево, только если его концы принадлежат разным компонентам, в противном случае в компоненте образуется цикл. Таким образом, если очередное ребро соединяет вершины, принадлежащие одной связной компоненте, то такое ребро не включается в строящееся остовное дерево и игнорируется алгоритмом.

Рассмотрим реализацию алгоритма на примере графа на рис.7.4[Окулов]. Потребуется массив меток вершин графа и массив ребер отсортированных по весам (рис. 7.6).

Начальные значения элементов массива меток M равны номерам соответствующих вершин. Ребро выбирается в каркас в том случае, если вершины, соединяемые им, имеют разные значения меток. В этом случае циклы не образуются. Для примера, приведенного выше, процесс изменения Mark показан на рис. .

Номер итерации	Ребро	Массив М
Нач. состояние		(1 2 3 4 5 6)
1	< 4, 1>	(1 2 3 1 5 6)
2	< 6, 1>	(1 2 3 1 5 1)
3	< 5, 2>	(1 2 3 1 2 1)
4	< 6, 3>	(1 2 1 1 2 1)
5	< 6, 5>	(1 1 1 1 1 1)
Рис. 7.7. Процесс изменения массива меток М

Реализация алгоритма:

1. Ищем ребро < v, w > с различными метками инцидентных ему вершин.

2. Копируем метку М[ v]  M[w] , если М[v] < M[w] и, наоборот,

М[w]  M[v] , если М[w] < M[v].

3. Повторяем эти действия n-1 раз (по числу ребер, которые образуют каркас).

В конце концов все элементы массива М приобретут значение метки равной 1 (рис. 7.7)

Процесс разметки начинается и распространяется с ребер, имеющих меньший вес, поэтому именно они в первую очередь будут включаться в каркас. Кроме того, ребра имеющие одинаковые метки в вершинах, инцидентных ему, исключаются в текущий момент из рассмотрения. При реализации алгоритма используется дополнительная процедура Marker.

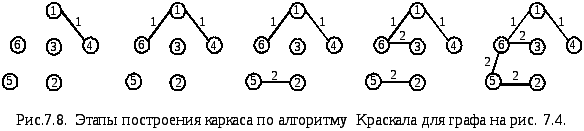
На рис. рис. 7.8. представлена последовательность этапов при построении компонент остовного дерева согласно жадному алгоритму. В качестве исходного графа выбран граф рис.7.4. Первоначально остовное дерево состоит из отдельных вершин исходного графа, жадный алгоритм постепенно добавляет к нему ребра, начиная с ребер с наименьшим весом. На рис. 7.8, б показаны 5 последовательных этапов построения остовного дерева согласно жадному алгоритму. На каждом этапе в остовное дерево включается новое ребро. Ребра, замыкающие цикл в уже построенной части, игнорируются алгоритмом.

Procedure Marker ( a, b :Integer ); { меньшую метку распространяет на все

вершины, инцидентные данному ребру (a,b)}

Var i, c :Integer;

Begin

If a > b Then Begin c := a; a := b; b := c; End; { делаем а <b }

For i := 1 To n Do

If M[ i ] = b Then M[ i ] := a;

End;

Procedure Kruskal;

Var i, j, v, w :Integer;

Begin

СОРТИРОВКА ребер R по возрастанию их весов;

For i :=1 To n Do M[ i ] := i;

For i :=1 To n-1 Do Begin

For j := 1 To n Do Begin

v :=R[ 1, j ]; w := R[ 2, j ];

If M[ v ] < > M[ w ] Then Break;

End;

Write( v:3, w:3); {вывод ребра}

Marker ( M[ v ], M[ w ] ); { меньшую метку распространяет на все}

End; {вершины, инцидентные данному ребру (a,b)}

End;

Общее время работы алгоритма Крускала составляет O(ElogE) (основное время уходит на сортировку). Скорость работы жадного алгоритма определяется скоростью, с которой будут выбраны и отсортированы все ребра графа, т. к. вся остальная работа обычно занимает меньше времени. Тем не менее для больших графов, построение и проверка деревьев компонент строящегося остовного дерева может занимать значительное время, если они вырождаются в линейные списки вершин, что вполне возможно в некоторых специфических ситуациях.

Алгоритм Прима. В этом алгоритме построение остовного дерева начинается с одной вершины, к которой затем добавляются ребра таким образом, чтобы каждое новое ребро одним своим концом опиралось в уже построенную часть дерева, а другой конец лежал бы в множестве еще не присоединенных к дереву вершин. Из всех таких ребер на каждом шаге выбирается ребро с наименьшим весом. Алгоритм Прима следует общей схеме алгоритма построения минимального остовного дерева: на каждом шаге мы добавляем к строящемуся остову безопасное ребро. Как и прежде воспользуемся «жадным» алгоритмом. Жадные алгоритмы действуют, используя в каждый момент лишь часть исходных данных и принимая лучшее решение на основе этой части. В нашем случае мы будем на каждом шаге рассматривать множество ребер, допускающих присоединение к уже построенной части остовного дерева, и выбирать из них ребро с наименьшим весом. Повторяя эту процедуру, мы получим остовное дерево с наименьшим весом. Отличие этого метода от метода Крускала заключается в том, что на каждом шаге строится дерево, а не ациклический граф (граф без циклов).

Для реализации введем две переменные множественного типа S0 и S1. Первоначально в S1 находятся все вершины графа, кроме начальной, а в S0 только начальная. Далее ищется ребро минимального веса, соединяющего вершину из S0 и одну из вершин v, принадлежащую S1. Найденное ребро включается в Q, а вершина v исключается из S1 и включается в S0. Далее повторяется поиск следующего ребра до тех пор, пока S1 не станет пустым.

На рис. 7.9 приведен пример построения каркаса по алгоритму Прима. Программная реализация алгоритма приведена ниже. В ней используется вспомогательная функция Extract_Min, которая ищет кратчайшее ребро, соединяющее вершины из S0 и S1.

S0, S1 :Set Of Byte; { S0 - множество выбранных вершин; }

{ S1 - множество невыбранных вершин;}

Function Extract_Min :Byte; {возвращает вершину v из S1 - самую }

Var i, j, w, v, Min :Integer; { « близкую» к множеству вершин S0 }

Begin Min := MaxInt;

For i := 0 To n-1 Do {перебор вершин в S0}

If i In S0

Then For j := 0 To n-1 Do {перебор вершин в S1}

If j In S1

Then If ( A[ i, j ] <> 0 ) And ( A[ i, j ] < Min )

Then Begin

Min := A[ i, j ];

w := i; v:=j;

End;

WriteLn( w :3, v :3 );

Extract_Min := v;

End;

Procedure Prima ( s :Byte ); { s – начальная вершина}

Var v :Byte;

Begin

S0 := [ s ];

S1 := [ 0..n – 1 ] - [ s ];

While S1 <> [ ] Do Begin

v := Extract_Min;

S0 := S0 + [ v ];

S1 := S1 - [ v ];

End;

End;

Время работы алгоритма Прима зависит от того, как реализована функция Extract_Min. Если вместо множеств S0 и S1 использовать очередь с приоритетами, то это время составит O(ElogV).

Алгоритмы имеют разную производительность на различных графах. Скорость работы алгоритма Крускала зависит, прежде всего, от количества ребер в графе и слабо зависит от количества вершин. Напротив, скорость работы алгоритма Прима определяется количеством вершин и слабо зависит от числа ребер. Следовательно, алгоритм Крускала следует применять в случае неплотных или разреженных графов, у которых количество ребер мало по сравнению с количеством ребер у полного графа. Если известно, что ребер в графе достаточно много, то для поиска минимального остовного дерева лучше применять алгоритм Прима.

Конечно, реальная скорость работы зависит и от представления графа, и от реализации основных операций над ним, и от реализации самих алгоритмов нахождения минимального остовного дерева, так что приведенные выше рекомендации носят очень приблизительный характер. Лучше всего поэкспериментировать немного самому, пробуя применить разные алгоритмы к различным графам.

9