8. Деревья.

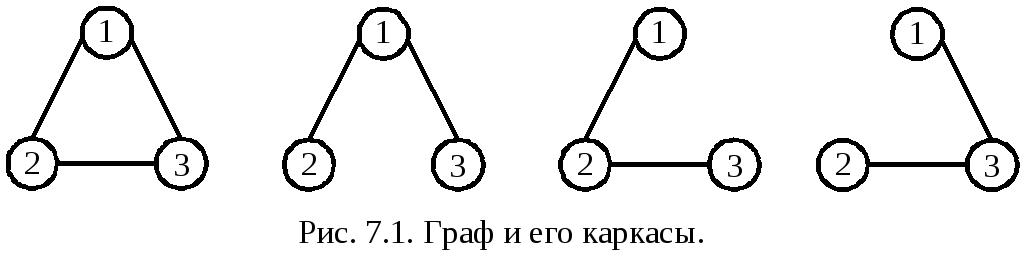
Деревом называют связный неориентированный граф без циклов. Иначе, связный граф, содержащий N вершин и N-1 ребер.

Для связного неориентированного графа G = < V, E > каждое дерево < V, T > , где TE называют стягивающим деревом (каркасом, остовом). Число различных каркасов полного связного неориентированного графа с N вершинами равно N^N-2 (Кэли)(рис. 7.1).

Рассмотрим два алгоритма нахождения каркаса (одного), основанных на методах просмотра графа поиском в глубину и в ширину.

7.1. Выделение дерева методом поиска в глубину и в ширину.

Известно, что как при поиске в глубину, так и при поиске в ширину просматриваются все вершины связного графа. Использование множества Т обеспечивает «подключение» очередного ребра к каркасу без образования циклов. Действительно, цикл образуется, если мы соединим две просмотренные вершины. Но в нашем случае «подключается» ребро, соединяющее просмотренную вершину с непросмотренной. И, наконец, по самой логике методов поиска в глубину и в ширину мы строим связный граф.

Для хранения ребер, образующих каркас, будем использовать структуру данных :

B :Array [1..2,1..n] Of Integer; { Столбец j матрицы B содержит две

вершины, инцидентные ребру j}

z :Integer; {z – индекс для B}

Построение остовного дерева (каркаса) методом поиска в глубину.

Procedure Tree_Gl ( v :Integer ); {рекурсивный вариант}

Var j :Integer;

Begin

T := T + [ v ];

Write(v:3);

For j := 1 To n Do

If ( A [v, j] <> 0 ) And Not ( T In [ j ] )

Then Begin Inc(z); B[1,z]:=v; B[2,z]:=j; {добавляем ветвь в остов}

Tree_Gl ( j );

End;

End;

Вызов: … s:=1; z:=0; T:=[ ]; Tree_Gl(s); Вывод матрицы B; …

Построение остовного дерева (каркаса) методом поиска в ширину.

Procedure Tree_SH ( v: Integer); { Поиск в ширину}

Var j :Integer;

Begin

r := 0; w := 1; Q[w] := v; { начальную вершину -> в очередь }

T:=[ v ];

While r < w Do Begin { пока очередь не пуста }

Inc( r ); v := Q[ r ]; {берем очередную вершину из очереди }

Write( v:3 );

For j := 1 To n Do { всех непросмотренных потомков этой вершины}

If (A[ v, j ] <> 0 ) And Not ( j In T ) { записываем в очередь }

Then Begin Inc( w ); Q[ w ] := j; T := T + [ j ];

Inc( z ); B[ 1, z ] :=v; B[ 2, z ] := j;

End;

End;

End;

Вызов: … s:=1; z :=0; SH_Obhod ( s ); Вывод матрицы B; …

Порождение всех каркасов графа

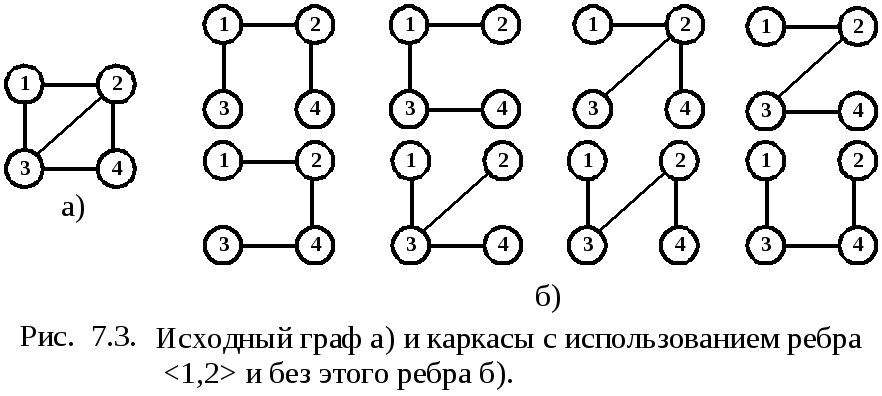
Для порождения очередного каркаса ранее построенные не привлекаются, используется только последний. Множество всех каркасов делится на два класс: содержащие выделенное ребро < v, u > и не содержащие его. Каркасы последовательно строятся в графах G_{< v, u >} и G - < v, u >. Каждый из графов G_{< v, u >} и G - < v, u > меньше, чем G. Последовательное применение этого шага уменьшает графы до тех пор, пока не будет построен очередной каркас либо графы станут несвязными и не имеющими каркасов. Пример графа и его каркасов в той последовательности, в которой они порождаются данным методом, приведен на рис 7.3.

Пусть:

Q :Array [1..nq] Of Integer; {очередь}

r, w :Integer; {r,w -индексы чтения и записи в очередь}

B :Array [1..2,1..n] Of Integer; {массив для ребер каракаса}

z :Integer; { индекс для массива B}

v – номер вершины, из которой выходит ребро;

u – номер вершины, начиная с которой следует искать очередное

ребро каркаса;

k – число ребер в каждом каркасе.

Procedure Ostov ( v, u :Integer ); {Построение всех каркасов графа

Var j :Integer; (рекурсивный алгоритм)}

Begin

If r >= w Then Exit;

j := u;

While ( j <= n ) And ( z < k ) Do Begin {просмотр ребер выходящих из v}

If (A[ v, j ] <> 0 ) And Not ( j In T ) Then Begin { есть ребро < v ,j >,

T := T + [ j ]; причем вершина j еще не просмотрена

Inc( z ); B [ 1, z ] := v; B [ 2, z ] := j; включаем это ребро в каркас

Q[ w ] := j; Inc( w ); а вершину j в очередь

Ostov ( v, j+1 ); и едем вперед}

Dec ( w ); T := T - [ j ]; Dec ( z ) ; {исключаем ребро из каркаса}

End;

Inc ( j );

End;

If z = k Then Begin WriteOstov( B, k ); Exit; End;

If j = n + 1 Then

Begin Inc( r ); {все ребра, выходящие из вершины v просмотрены,

Ostov( Q[ r ], 1 ); переходим к следующей вершине из очереди и

Dec( r ); так до тех пор, пока не будет построен каркас}

End;

End;

Begin … Q[1]:=1; r:=1; w:=2; z:=0; k:=3; T :=[1]; Ostov(1,2); … End;