Алгоритм:

Пусть мы находимся в городе с номером v.

Шаг 1. Если расстояние (стоимость), пройденное коммивояжером до города с номером v, не меньше стоимости найденного ранее наилучшего решения (bC), то следует выйти из данной ветви дерева перебора.

Шаг 2. Если рассматривается последний город маршрута (осталось только вер­нуться в первый город), то следует сравнить стоимость найденного нового реше­ния со стоимостью лучшего из ранее найденных. Если результат сравне­ния по­ложительный, то значения bC и bW следует изменить и выйти из этой ветви де­рева перебора.

Шаг 3. Пометить город с номером v как рассмотренный, записать этот номер по значению k в массив W.

Шаг 4. Рассмотреть пути коммивояжера из города v в ранее не рассмотренные го­рода. Если такие города есть, то перейти на эту же логику с измененными значе­ниями v, k,C, иначе на следующий шаг.

Шаг 5. Пометить город v как нерассмотренный и выйти из данной ветви де­рева пе­ребора.

Представляется разумным предварительно отсортировать по возрастанию строки матрицы расстояний, чтобы выбор следующего за v города начинался с наи­бо­лее перспективных (ближних) городов. Так как непосредственная сорти­ровка элементов матрицы расстояний привела бы к их перемещениям, использу­ется вспо­могательная матрица индексов B. (Ниже приведены матрицы А и В (после сорти­ровки элементов каждой строки матрицы А) и пример выполнения программы.

А В
×	27	43	16	30	26		4	6	2	5	3	1
7	×	16	1	30	25		4	1	3	6	5	2
20	13	×	35	5	0		6	5	2	1	4	3
21	16	25	×	18	18		2	5	6	1	3	4
12	46	27	48	×	5		6	1	3	2	4	5
23	5	5	9	5	×		2	3	5	4	1	6
Символом × обозначено бесконечное расстоя­ние. Опт. путь: 1 - 4 - 3 - 5 - 6 - 2 Стои­мость: 63

Procedure CVoyager (v, k, C :Integer); {Поиск оптимального пути}

{v – номер текущего города; k - счетчик числа пройденных городов;

C–cтоимость теку­щего решения}

Var i :Integer;

Begin

If C > bC Then Exit; {Стоимость текущего решения превышает

стоимость лучшего из ранее полученных }

If k = n Then Begin; {Пoследний город пути.

C:=C+A[v,1]; W[n] := v; Доформировываем решение и сравниваем его

If C < bC Then Begin bC := C; bW := W; End; с лучшим из ранее

Exit; полученных.}

End;

P[v] := False; {Город с номером v пройден,

W[k] := v; записываем его номер в путь коммивояжера}

For i:=1 To n Do {Поиск продолжения пути из города v}

If P[B[v, i] ] Then CVoyager (B[v,i], k+1, C + A[v, B[v,i] ]);

P[v]:=True;

End;

{Головная программа }

Begin

….

SortA;

bC:=Maxint;

CVoyager (1,1,0);

PrintWay;

….

End.

7.3. Динамическое программирование.

Динамическое программирование - один из методов сокращения перебора при решении задач оптимиза­ции. В названии «Динамическое программирование» под «программированием» понимают «принятие решений», «планирование», а слово «динамическое» указывает на существенную роль времени и порядка выполнения операции в рассматриваемых процессах и методах.

Существует достаточно много задач, которые требуют перебора большого количества (а то и всех ) комбинаций данных (последовательностей) для выбора оптимального решения. Такие задачи очень трудоемки для ЭВМ, поэтому существуют методы ограниченного перебора (оптимизация решения задачи в процессе решения). Динамическое программирование определяет оптимальное решение n-мерной задачи путем ее декомпозиции на n этапов, каждый из которых представляет собой подзадачу относительно одной переменной. Оптимальное решение строится постепенно, шаг за шагом. На каждом шаге оптимизируется решение только этого шага, но решение выбирается с учетом последствий, так как решение, оптимальное для этого шага, может привести к неоптимальному решению всей задачи, т.е. оптимальное решение задачи содержит оптимальные решения ее подзадач. Вычислительное преимущество такого подхода состоит в том, что мы занимаемся решением одномерных оптимизационных задач подзадач вместо большой n-мерной задачи. Метод основывается на сформулированном Р. Беллманом принципе оптимальности: отрезок оптимального процесса от любой его точки до конца процесса сам является оптимальным процессом с началом в данной точке. Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Использование этого принципа гарантирует, что решение, выбранное на любом шаге, является не локально лучшим, а лучшим с точки зрения задачи в целом.

Выделим особенности модели динамического программирования:

• задача оптимизации интерпретируется как n-шаговый процесс управления;

• целевая функция равна сумме целевых функций каждого шага;

• выбор управления на k-м шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи);

Динамическое программирование применяется для решения сложных задач планирования развития экономических и других систем, когда множество возможных вариантов развития такой системы удается представить в виде ориентированного графа. Ориентированным называется граф, в котором дуги имеют направления и перемещаться по ним можно только в заданном направлении. Простейшая задача динамического программирования представлена на рис. 7.9.

Необходимо переместиться из точки А в точку В. Все возможные пути перемещения указаны стрелками. Известна длина каждой дуги. Необходимо найти кратчайший путь. Вся процедура разбита на шаги. На первом шаге можно продвинуться из А в одну из точек a, b или с. На втором шаге из любой точки – a, b или с – можно попасть в любую из точек d, f, h. Наконец, на последнем шаге из любой точки – d, f, h – осуществляется перемещение в В.

Обозначим:

– длина соответствующей дуги;

– длина кратчайшего пути, ведущего из точки А в соответствующую точку, указанную в индексе при F – это и есть целевая функция.

Оптимальный путь можно выявить полным перебором, просчитав длины всех путей и сравнив их между собой. Посчитаем, сколько различных путей существует в нашей простой задаче. Из А в каждую из точек – a, b, c – ведет по одному пути. В каждую из точек d, f, h ведут три пути, а всего в конце второго шага имеется 9 путей. На последнем шаге количество путей не увеличивается. Конечно, можно сравнить по всей длине 9 путей. Но с ростом количества шагов и количества точек на каждом шаге число вариантов резко возрастает. Пусть m – число шагов, n – число точек на каждом шаге. В конце первого шага будет n вариантов (по одному на каждую точку). В конце второго шага будет n². Т. к. на последнем шаге число вариантов не увеличивается, всего будет n^m-1 вариантов. При значительных величинах m и n перебор всех вариантов становится невозможным даже на компьютере.

Основная идея динамического программирования заключается в сокращении перебора за счет отбрасывания бесперспективных путей. В любой точке, где сходится несколько путей, их можно сравнить между собой по длине, оставить лучший, запомнить его и его длину, а остальные отбросить. На рис. 7.9. в точке d сходятся 3 пути (из a, b и c), для каждого из них вычисляется длина, лучший путь запоминается, а два других отбрасываются.

Алгоритм расчета следующий.

1. Делается первый шаг от начала.

2. Берется первая точка а.

3. Вычисляется . Запоминаются F_a и точка А – откуда пришел лучший путь (он здесь единственный).

Берется следующая точка b и для нее проделываются все те же процедуры, что и для а.

4. После расчетов для точки c делается следующий шаг.

5. Берется точка d. В нее входят 3 пути. Для каждого из них вычисляется ,,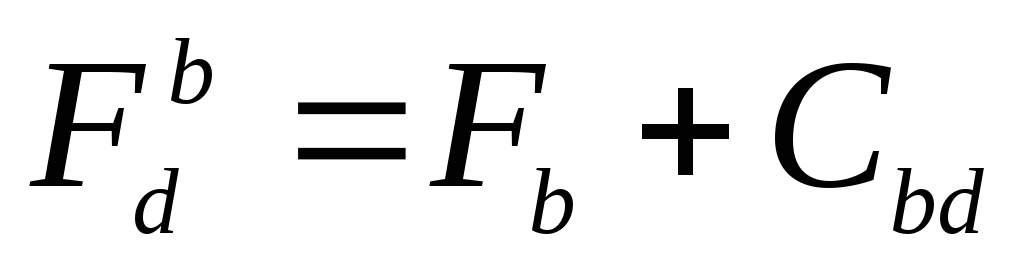_. Запоминается как F_d меньшая из вычисленных длин и точка, откуда ведет путь. Пусть и , тогда , запоминается точка с. Это значит, что путь через точку с в d сохраняется для дальнейшего анализа, а пути в d через a и b отбрасываются.

6. После рассмотрения очередной точки осуществляется переход к следующей точке на данном шаге. Когда на рассматриваемом шаге все точки закончились, делается следующий шаг и т.д.

7. В точке В из трех сходящихся в ней путей выбирается лучший.

8. Проходя в обратном направлении, восстанавливают оптимальный путь. Например, в точке В лучшим оказался путь из d, а в d – из c, а в c ведет единственный путь из А. Тогда оптимальный путь проходит через точки A–c–d–B.

При таком процессе в данном примере приходится сравнивать 12 путей (по 3 на каждую из точек d, f, h, В). Но сравнения проводятся на одном шаге, а не на всей длине, как это было бы при полном переборе. Перебор существенно сокращается.

Важный классом функций, заведомо удовлетворяющих принципу Беллмана, являются аддитивные функции, равные сумме некоторых функций, зависящих только от соседних компонент последовательности:

Рассмотрим программную реализацию метода динамического программирова­нии на конкретном примере.

Пример. В таблице размером n*n, где n < 13, клетки заполнены случайным обра­зом цифрами от 0 до 9. Предложить Чебурашке алгоритм, позволяющий найти маршрут из клетки (1,1) в клетку (n,n) и удовлетворяющий следующим усло­виям:

1. любые две последовательные клетки в маршруте имеют общую сто­рону;

2. количество клеток маршрута минимально;

3. сумма цифр в клетках маршрута максимальна.

Алгоритм. Будем искать наилучшие пути, идущие из клетки (1,1) во все остальные клетки таблицы, в частности и в клетку (n,n). Для этого в некоторой вспомога­тельной таблице B того же размера, что и А, будем отмечать суммы цифр опти­мальных путей, ведущих в соответствующие клетки. Так в клетке(1,1) таблицы В окажется число А(1,1), потому что путь, ведущий в нее , состоит из одной клетки. Так же легко заполняются клетки (1,2) и (2,1) таблицы В. В них тоже ведут единственные пути. и суммы цифр вдоль них равны А(1,1)+А(1,2) и А(1,1)+А(2,1) соответственно.

Поясним сказанное на конкретном примере. Пусть таблица А размером 5*5 имеет вид, представленный на рис.2. Нумерация клеток идет от левого верх­него угла. Проследим за заполнением таблицы В. О клетках (1,2) и (2,1) уже го­ворилось. Чтобы заполнить клетку (2,2), заметим, что в нее можно попасть либо из клетки (1,2), либо из клетки (2,1). Следовательно, в клетку (2,2) таблицы В надо записать либо число В(1,2)+А(2,2), либо число В(2,1)+А(2,2), в зависимо­сти от того, какое из них больше. Заполнение остальных клеток таблицы В ана­логично.

А 754 135 9 4 1 3 2 3 5 1 2 1 3 1 2 0 4 6 7 2 1	B 4 −− 7 −− 12 −− 19 −− 24 | | | 5 16 −− 20 −− 21 27 | | | | 7 19 25 −− 26 29 | | | | | 8 22 26 28 29 | | 12 28 −− 35 −− 37 −− 38
Рис.

Если путь, ведущий в эту клетку один, то в клетку вписывается сумма цифр вдоль этого пути. Такими клетками являются клетки вида (1,J) и (J,1).

Если же в клетку (I,J) можно попасть из клеток для которых подсчитаны значения В, то необходимо выбрать М=mах(B(I,J-1), B(I-1,J)) и записать в клетку B(I,J) число М+А(I,J).

Клетку B(I,J) соединим чертой с той клеткой, где был достигнут макси­мум М. Для нахождения искомого маршрута достаточно пройти из клетки (n,n) в клетку (1,1) по черточкам. Таким образом искомый оптимальный путь выглядит так: 1,1→1,2→2,2→3,2→4,2→5,2→5,3→5,4→5,5

Program DinPro;

Const n=5;

a :Array[1..n,1..n] Of Integer=((4,3,5,7,5),

(1,9,4,1,3),

(2,3,5,1,2),

(1,3,1,2,0),

(4,6,7,2,1));

Var b :Array[0..n,0..n] Of Integer;

i, j:integer;

Procedure Way (i ,j :Integer);

Begin

If (i < >1)Or(j < > 1)Then

If b[i, j-1] > b[i-1,j]

Then Way(i, j-1)

Else Way(i-1, j);

Write(i:3,',',j);

End;

Begin

FillChar(b,2*(n+1)*(n+1),0);

For i:= 1 To n Do

For j:= 1 To n Do b[i,j] := a[i,j] + Max(b[i-1,j], b[i,j-1]);

Way(n,n);

ReadKey;

End.

Замечания.

1. Принцип оптимальности является основой поэтапного решения задачи динамического программирования. Несмотря на то, что этот принцип не содержит информации о способах решения подзадач на каждом этапе, его применение существенно облегчает решение многих сложных задач, которые нельзя решить другими методами. Укажем два признака, характерных для задач, решаемых методами динамического программирования.

1. задача обладает свойством оптимальности для подзадач, т. е. оптимальное решение задачи содержит оптимальные решения ее подзадач.

2. задача имеет перекрывающиеся подзадачи, т. е. при рекурсивном решении мы многократно выходим на одни и те же подзадачи.

   2. Вычисления в динамическом программировании выполняются рекуррентно в том смысле, что оптимальные решения одной подзадачи используются в качестве исходных данных для следующей подзадачи. Способ выполнения рекуррентных вычислений зависит от того, как выполняются декомпозиции исходной задачи. В данной ситуации возможны несколько вариантов. Первый из них это проводить вычисления последовательно от первого до последнего этапа, такая последовательность известна как алгоритм прямой прогонки. Задача может быть решена с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от последнего этапа до первого. Очевидно, что алгоритмы прямой и обратной прогонки приводят к одному и тому же решению. Обычно более логичным представляется использовать алгоритм прямой прогонки, но в общем случае алгоритм обратной прогонки может быть более эффективным с вычислительной точки зрения.

   3. Методы динамического программирования являются составной частью методов, используемых в исследовании операций и применяются как в задачах оптимального планирования, так и при решении различных технических проблем (например, в задачах определения оптимальных размеров ступеней многоступенчатых ракет, в задачах оптимального проектирования прокладки дорог и др.).

   4. Беллманом сформулированы и условия, при которых принцип верен. Основное требование - процесс управления должен быть без  обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги. Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.