5.7. Удаление в дереве сортировки

Для обеспечения нормальной работы с деревом поиска на практике, - это удаление узлов из дерева. Если эта задача будет решена, то перемещение узла по дереву из-за изменения его значения - может быть решена удалением одного узла и вставкой нового вместо него.

П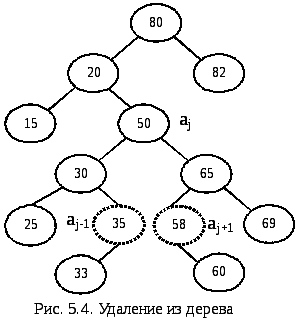роще всего удалить узел, если он находится в листе дерева. В этом случае достаточно лишь убрать из дерева указатель на этот узел. Разумеется, сначала придется произвести поиск этого узла в дереве. Не очень сильно отличается от этого и случай, при котором удаляемый узел имеет лишь один указатель на поддерево (левое или правое). Очевидно, что и в этом случае для удаления узла достаточно изменить лишь один указатель на удаляемый узел, заменив его указателем на его единственное поддерево.

Для того чтобы решить задачу удаления узла в общем виде, ее сводят к одной из описанных простых ситуаций. Для этого в одном из поддеревьев удаляемого узла находят узел, значение которого наиболее близко к значению в удаляемом узле: максимальное значение в левом поддереве или минимальное значение в правом поддереве. Очевидно, что в обоих случаях такое ближайшее значение обязательно будет расположено либо в листе дерева, либо в узле, имеющем только одно поддерево. После этого делают подмену: удаляют вместо нужного узла один из найденных ближайших узлов, а значение, которое в нем содержалось, переносят в узел, который требовалось удалить. Очевидно, что структура дерева поиска при этом не нарушится и оно останется отсортированным.

Поэтому есть два равноценных (симметричных) вари­анта алгоритмов удаления – один ориентируется на замену удаляемого элемента a_j элементом a_j+1, другой - элементом a_j-1 (рис. ).

Рассмотрим пример удаления из дерева, когда удаляемое значение замещается из самой правой вершины своего левого поддерева. Проце­дуры поиска и удаления реализованы рекурсивно.

Function DelUzl(Var h: u): Integer; {функция удаления узла в общем случае}

Var t: u;

Begin

If h^.R = Nil

Then Begin DelUzl := h^.i; { Результат функции }

t := h; { Запоминаем узел для последующего удаления }

h := h^.L; { продвигаемся дальше }

Dispose(t); { удаляем бывший корень }

End

Else DelUzl := DelUzl (h^.R);

End;

{Удаление в отсортированном бинарном дереве}

Рrocedure DelBT (Var h: u; a: integer);

Var t: u;

Begin

If h=Nil Then Writeln (‘Элемента нет’);

Else If a < h^. i Then DelBT ( h^. L, a ) {поиск влево}

Else If a > h^. i Then DelBT (h^. R, a) {поиск вправо}

Else Begin t := h; {нашли удаляемый узел}

{нет R –ссылки} If t^. R = Nil Then Begin h := t^. L; Disрose ( t ); End

Else If t^. L = Nil

{ нет L –ссылки} Then Begin h:=t^. R; Disрose (t); End

{имеются R и L –ссылки} Else h^.i := DelUzl(h^.L);

End;

End;