Lektsii_TRPO / BT_Представление БД в массиве

Представление БД в массиве.

Для создания бинарного дерева используются два вспомогательных массива (ин­дексы вершин его правого и левого поддерева) и переменная, в которой хранится ин­декс корня. Признак пустой ссылки — отрицательное число или нуль. Напри­мер, дерево, приведенное на рис. 5.9, можно представить следующим образом:

1 2 3 4 5 6 7 8

10 25 20 6 21 8 1 30 - массив данных

4 3 -1 7 -1 -1 -1 -1 - левая ссылка

2 8 5 6 -1 -1 -1 -1 - правая ссылка

1 - индекс корневого элемента дерева.

БД - пирамида

Иногда используются и другие способы представления деревьев. Например, в некоторых случаях связи между узлами дерева можно вообще не представлять с помощью указателей, а “вычислять”, если узлы дерева образуют регулярную структуру, не меняющуюся или меняющуюся очень мало в процессе работы с деревом. Такое дерево называют пирамидой или кучей.

Рис. 1.5. Пронумерованное дерево - пирамида

Пусть узлы бинарного дерева пронумерованы, начиная с корня и далее вниз по иерархическим уровням, как показано на рис. 1.5. При этом узлы расположены настолько плотно, что предком узла с номером i всегда является узел с номером i/2. В этом случае узлы дерева можно расположить в массиве, причем местоположение каждого узла будет задано его индексом в массиве, а максимальное число узлов задается сразу же при создании дерева.

Ниже пирамида используется для одного из способов сортировки элементов массива - так называемой пирамидальной сортировки.

Пирамидальная сортировка ( HeapSort ).

Пирамида – помеченное корневое двоичное дерево заданной высоты h, обладающее следующими тремя свойствами:

1. Каждая терминальная вершина имеет высоту h или h-1.

2. Каждая терминальная вершина высоты h находится слева от любой терминальной вершины высоты h-1.

3. Метка любой вершины больше метки любой следующей за ней вершины.

Дерево, удовлетворяющее этим условиям и ее отображение в одномерный массив приведено на рис. .

27

9

14

8

5

11

7

2

3

Замечания.

1. Пирамида легко отображается в одномерный массив (а не в структуру со ссылками) по правилу: две непосредственно следующие за вершиной a[i] вершины помещаются в a[ 2*i ] и a[ 2*i +1 ].

2. Если 2*i > n (n – длина массива), то за вершиной a[i] не следуют другие вершины и она является терминальной вершиной пирамиды.

3. Если массив а представляет собой пирамиду, то он легко сортируется.

Алгоритм пирамидальной сортировки. Пусть массив а – пирамида.

1. Переставить местами a[1] и a[n].

2. Установить n:=n-1 (т.е. вычеркиваем абсолютный максимум = 27 ).

3. Преобразовать полученное дерево в пирамиду по правилу: повторять перестановку нового корня с большей из двух непосредственно следующих за ним вершин до тех пор, пока он не станет больше, чем обе вершины, непосредственно за ним следующие.

4. Повторять шаги 1,2,3 до тех пор, пока не получится n=1.

Процесс преобразования массива а в пирамиду после первого обмена a[1] ↔ a[n] показан на рис. :

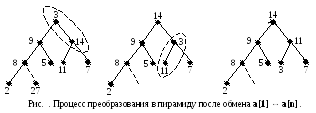
Поскольку для такой процедуры сортировки на входе требуется пирамида, нужен алгоритм для преобразования произвольного массива целых чисел в пирамиду. Такой алгоритм использует шаг 3 ранее описанного процесса. Начнем с предположения, что исходный массив расположен в корневом двоичном дереве, как было бы в случае, если в массиве была бы размещена пирамида. Проходим справа налево весь массив проверяя, больше ли a[i], чем a[2*i] и a[2*i+1] для i= n div 2. Если для какого-то значения i a[i] не больше, чем a[2*i] и a[2*i+1], то применяем процедуру шага 3 и переставляем a[i] с большим из элементов a[2*i] и a[2*i+1] (рис. .).

индекс	1	2	3	4	5	6	7	8	9
массив а	5	3	7	27	9	11	14	2	8
i=4	5	3	7	27	9	11	14	2	8
i=3			7			11	14
обмен			14			11	7
i=2		3		27	9
обмен		27		3	9
				3				2	8
обмен				8				2	3
i=1	5	27	14
обмен	27	5	14
		5		8	9
обмен		9		8	5
пирамида	27	9	14	8	5	11	7	2	3

Таким образом для реализации алгоритма пирамидальной сортировки необходима вспомогательная процедура Heap ( a, j, m), которая ставит элемент a[j] на надлежащее ему место в пирамиде с элементами a[1..m] (m ≥ 3, 1≤ j ≤ m):

HEAP

While ((2j +1) ≤ m ) And ( (a_j < a_2j ) Or (a_j < a_2j+1 )) Do

If a_2j > a_2j+1 Then Обмен a_j ↔ a_2j

Else Обмен a_j ↔ a_2j+1 ;

End -Do;

If (2j = m) And (a_j < a_2j) { особый случай, когда 2j = m }

Then Обмен a_j ↔ a_2j ;

End - HEAP;

Тогда алгоритм сортировки HeapSort( a, n ) для массива a[1..n] (n ≥ 2) выглядит следующим образом:

HeapSort

i := n Div 2; { инициализация}

m := n;

While i ≥ 1 Do { создание пирамиды}

HEAP(a, i, m);

i := i - 1;

End-Do;

While m ≥ 1 Do { сортировка }

Обмен a₁ ↔ a_m ;

m := m - 1;

HEAP( a, 1, m );

End-Do;

End-HeapSort;

Замечание. На первый взгляд вовсе не очевидно, что такой алгоритм сортировки дает хорошие результаты. Ведь в конце концов большие элементы, прежде чем попадут на свое место в левой части, несколько раз перемещаются. И действительно, процедуру не рекомендуется применять для небольшого, вроде нашего примера, числа элементов. Для больших же n этот алгоритм очень эффективен; чем больше n, тем лучше он работает.

Сложность алгоритма ≈ O(n Ln(n) ).

Program Piram_Sort; {Сортировка пирамиды}

Uses CRT;

Const n=9; a:Array[1..n]Of Integer=(8,21,29,6,24,16,11,22,3);

{-----------------------------------}

Procedure Swap ( i, j :Integer );

Var c:Integer;

Begin c:=a[i]; a[i]:=a[j]; a[j]:=c; End;

{-----------------------------------}

Procedure Heap ( i, m :Integer);

Function TmL:Boolean; Begin TmL:=a[i] < a[2*i]; End; {T<L}

Function TmR:Boolean; Begin TmR:=a[i] < a[2*i+1]; End; {T<R}

Function LbR:Boolean; Begin LbR:=a[2*i] > a[2*i+1]; End; {L>R}

Begin

While (2*i+1 <= m)And( TmL Or TmR ) Do

If LbR Then Begin Swap ( i, 2*i ); i:=2*i; End

Else Begin Swap ( i, 2*i+1); i:=2*i+1; End;

If ( 2*i = m ) And TmL Then Swap ( i, 2*i );

End;

{-----------------------------------}

Procedure HeapSort;

Var k :Integer;

Begin

For k:=n Div 2 DownTo 1 Do Heap(k,n);

For k:=n DownTo 1 Do

Begin Swap(1, k); Heap(1,k-1); Print; End;

End;

1 2 3 4 5 6 7 8 9

Исх. массив 8 21 11 6 24 16 29 22 22

Пирамида 29 24 16 22 21 8 11 22 6

Процесс сортировки

1 2 3 4 5 6 7 8 9

24 22 16 22 21 8 11 6 29

22 22 16 6 21 8 11 24 29

22 21 16 6 11 8 22 24 29

21 11 16 6 8 22 22 24 29

16 11 8 6 21 22 22 24 29

11 6 8 16 21 22 22 24 29

8 6 11 16 21 22 22 24 29

6 8 11 16 21 22 22 24 29

6 8 11 16 21 22 22 24 29

Тогда БД можно построить с помощью следующей рекурсивной процедуры:

{Подсчет числа терминальных вершин}

Procedure KolTerm( h : u; Var k : Integer );

Begin

IF h <> Nil Then Begin

KolTerm( h^.L, k );

IF (h^.L = Nil) And (h^.R = Nil) Then Inc(k);

KolTerm( h^.R, k );

End;

End;

{-------------------------------------}

{Удаление дерева с освобождением памяти }

PROCEDURE Del_T(h : u );

Begin

IF h<>Nil Then Begin

Del_T (h^.L);

Del_T (h^.R);

Dispose(h);

End;

End;