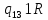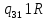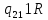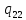4. Варианты заданий

Вариант 1

1. Выяснить, применима ли машина Тьюринга Т, задаваемая программой П, к слову Р. Если применима, то выписать результат применения машины Т к слову Р. Предполагается, что — началь­ное состояние,— заключительное состояние и в начальный момент головка машины обозревает самую левую единицу на ленте:

a) б)в)

2. Показать, что для всякой машины Тьюринга существует эквивалентная ей машина, в программе которой отсутствует сим­вол S.

3. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1
2	—		—	—	—

i=3, T:

4. Построить машину Тьюринга, вычисляющую функцию :

5. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

Вариант 2

1. Выяснить, применима ли машина Тьюринга Т, задаваемая программой П, к слову Р. Если применима, то выписать результат применения машины Т к слову Р. Предполагается, что — началь­ное состояние,— заключительное состояние и в начальный момент головка машины обозревает самую левую единицу на ленте:

a) б)в)

2. Показать, что по всякой машине Тьюринга можно построить эквивалентную ей машину, в программе которой не содержится за­ключительных состояний.

3. Найти результат применения машины к слову Р (— заключительное состояние маши­ны, а— заключительное состояние машины):

0
1

0
1

0
1

.

4. Построить машину Тьюринга, вычисляющую функцию :

5. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

Вариант 3

1. Выяснить, применима ли машина Тьюринга Т, задаваемая программой П, к слову Р. Если применима, то выписать результат применения машины Т к слову Р. Предполагается, что — началь­ное состояние,— заключительное состояние и в начальный момент головка машины обозревает самую левую единицу на ленте:

a) б)в)

2. Показать, что для всякой машины Тьюринга Т в алфави­те А существует счетно-бесконечное множество эквивалентных ей машинв том же алфавитеА, отличающихся друг от друга своими программами.

3. Найти результат применения машины к слову Р (— заключительное состояние маши­ны, а— заключительное состояние машины):

0
1

0
1

0
1

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

Вариант 4

1. Выяснить, применима ли машина Тьюринга Т, задаваемая программой П, к слову Р. Если применима, то выписать результат применения машины Т к слову Р. Предполагается, что — началь­ное состояние,— заключительное состояние и в начальный момент головка машины обозревает самую левую единицу на ленте:

a) б)в)

2. Сколько существует неэквивалентных машин Тьюринга в алфавите программы которых содержат только по одной ко­манде?

3. Найти результат применения машины к слову Р (— заключительное состояние маши­ны, а— заключительное состояние машины):

0
1

0
1

0
1

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

Вариант 5

1. Выяснить, применима ли машина Тьюринга Т, задаваемая программой П, к слову Р. Если применима, то выписать результат применения машины Т к слову Р. Предполагается, что — началь­ное состояние,— заключительное состояние и в начальный момент головка машины обозревает самую левую единицу на ленте:

a) б)в)

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• Начав работу с последней единицы массива из единиц, маши­на «сдвигает» его на одну ячейку влево, не изменяя «остального содержимого» ленты. Головка останавливается на первой единице «перенесенного» массива.

3. Найти результат применения машины к слову Р (— заключительное состояние маши­ны, а— заключительное состояние машины):

0
1

0
1

0
1

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

Вариант 6

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина имеет одно состояние, одну команду и применима к любому слову в алфавите .

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• Начав двигаться вправо от какой-то «начальной» ячейки, го­ловка «находит» первую при таком перемещении ячейку с единицей (если такая ячейка «встретится на пути») и, сделав «один шаг» вправо, останавливается на соседней ячейке. Если в «начальной» ячейке записана единица, то головка останавливается на соседней справа ячейке. Содержимое ленты не меняется.

3. Используя машины ипостроить опера­торную схему алгоритма₤ (здесь — заключительные состояния соответствующих машин):

0
1			—

0
1

0	—
1

0
1

0
1

₤: .

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

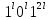(функционирование машины не должно зависеть от зна­чения l).

Вариант 7

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина имеет две команды, не применима ни к какому слову в алфавите и зона работы на каждом слове бесконечная.

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• Машина начинает работу с самой левой непустой ячейки и отыскивает единицу, примыкающую с левой стороны к первому слева массиву из трех нулей («окаймленному» единицами). Головка остана­вливается на найденной единице (если такая есть). Содержимое ленты не меняется.

3. Используя машины ипостроить опера­торную схему алгоритма₤ (здесь — заключительные состояния соответствующих машин):

0
1			—

0
1

0	—
1

0
1

0
1

₤:

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(функционирование машины не должно зависеть от зна­чения l).

Вариант 8

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина имеет две команды, не применима ни к какому слову в алфавите и зона работы на любом слове ограничена одним и тем же числом ячеек, не зависящим от выбранного слова.

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• При заданном головка машины, начав работу с произ­вольной ячейки, содержащей единицу, двигается вправо до тех пор, пока не пройдет подряднулей. Головка останавливается на первой ячейке за этиминулями, напечатав в ней 1. Остальное содержимое ленты не меняется.

3. Используя машины ипостроить опера­торную схему алгоритма₤ (здесь — заключительные состояния соответствующих машин):

0
1			—

0
1

0	—
1

0
1

0
1

₤:

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(n массивов единиц, n ≥ 1), где n - фиксировано, l - произвольное.

Вариант 9

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина имеет три команды, применима к словам и не применима к словам.

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• При заданном головка машины, начав работу с какой-то ячейки и двигаясь вправо, ставит подрядединиц и останавливается на последней из них.

3. По операторной схеме алгоритма ₤ и описанию машин, входящих в нее, построить программу машины Т, задаваемой этой схемой, и найти результат применения машины Т к слову Р:

₤

0
1
2	—

0
1
2	—

0
1		—
2		—	—

(начальные состояния машин а заключительные — ).

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(n массивов единиц, n ≥ 1), где l - фиксировано, n - произвольное.

Вариант 10

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина имеет пять команд, применима к словам и не применима к словам.

2. По словесному описанию машины Тьюринга построить ее программу (в алфавите

• При заданном головка машины, двигаясь вправо от какой- либо пустой ячейки, находит первый при таком перемещении массив, содержащий не менееединиц, стирает в нем первыеединиц и останавливается на самой правой из ячеек, в которых были стертые единицы. Остальное содержимое ленты не меняется.

3. По операторной схеме алгоритма ₤ и описанию машин, входящих в нее, построить программу машины Т, задаваемой этой схемой, и найти результат применения машины Т к слову Р:

₤

0
1

0	—			—
1

0
1			—

(начальные состояния машин а заключительные — ).

4. Построить машину Тьюринга, правильно вычисляющую функцию :

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(l - фиксированное, меняется α, ).

Вариант 11

1. Построить в алфавите машину Тьюринга, обладающую следующими свойством (предполагается, что в начальный момент головка обозревает самый левый символ слова, и в качестве пустого символа берется 0):

• машина применима к словам , где, и не применима к словам, где.

2. Построить композицию машин Тьюрингапо паре состоянийи найти результат применения композициик словуР (—заключительное состояние машины):

0
1

0
1

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

Вариант 12

1. По заданной машине Тьюринга Т и начальной конфигура­ции К₁ найти заключительную конфигурацию ( — заключительное состояние):

a) б)

2. Построить композицию машин Тьюрингапо паре состоянийи найти результат применения композициик словуР (—заключительное состояние машины):

0
1

0
1

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

Вариант 13

1. По заданной машине Тьюринга Т и начальной конфигура­ции К₁ найти заключительную конфигурацию ( — заключительное состояние):

a) б)

2. Построить композицию машин Тьюрингапо паре состоянийи найти результат применения композициик словуР (—заключительное состояние машины):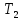

0
1

0
1

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

Вариант 14

1. По заданной машине Тьюринга Т и начальной конфигура­ции К₁ найти заключительную конфигурацию ( — заключительное состояние):

a) б)

2. Построить композицию машин Тьюрингапо паре состоянийи найти результат применения композициик словуР (—заключительное состояние машины):

0
1

0
1

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется 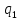, а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(функционирование машины не должно зависеть от зна­чения l).

Вариант 15

1. По заданной машине Тьюринга Т и начальной конфигура­ции К₁ найти заключительную конфигурацию ( — заключительное состояние):

a) б)

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1				—	—

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(n массивов единиц, n ≥ 1), где n - фиксировано, l - произвольное.

Вариант 16

1. По заданной машине Тьюринга Т и начальной конфигура­ции К₁ найти заключительную конфигурацию ( — заключительное состояние):

a) б)в)

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1				—	—

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(n массивов единиц, n ≥ 1), где l - фиксировано, n - произвольное.

Вариант 17

1. Построить в алфавите машину Тьюринга, переводящую конфигурациив конфигурации:

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1				—	—

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. По программе машины Тьюринга Т записать аналитическое выражение для функций и, вычисляемых машиной Т (в качестве начального состояния берется , а в качестве заключитель­ного —):

0			—
1

T:

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Заданный l-кратный код набора преобразуется в решетчатый код

(l - фиксированное, меняется α, ).

Вариант 18

1. Построить в алфавите машину Тьюринга, переводящую конфигурациив конфигурации:

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1				—	—

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. Какие одноместные функции вычисляются всеми такими ма­шинами Тьюринга в алфавите , программы которых содержат только по одной команде?

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

Вариант 19

1. Построить в алфавите машину Тьюринга, переводящую конфигурациив конфигурации:

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

Вариант 20

1. Построить в алфавите машину Тьюринга, переводящую конфигурациив конфигурации:

2. Найти результат применения итерации машины Т по паре состояний (,) к слову Р (заключительными состояниями являют­ся и):

0
1

i=1, T:

3. Построить машину Тьюринга, вычисляющую функцию :

4. На решетке с шагом l смоделировать работу машины Т, вычисляющей функцию

5. Построить машину Тьюринга, преобразующую один машин­ный код в другой. Решетчатый код с заданной совокупностью слов, расположен­ных на соответствующих решетках (1-й, 2-й и т.д.), преобразуется в l-кратный код с указанным значением l:

СПИСОК ЛИТЕРАТУРЫ

1. Галиев Ш.И. Математическая логика и теория алгоритмов. Казанский технический университет им. А.Н. Туполева. 2002. – 262 с.

2. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. Издание третье. М.: Физматлит. 1995. – 246 с.

3. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. Издание пятое. М.: Физматлит. 2004. – 256 с.

4. Гуц А.К. Математическая логика и теория алгоритмов. Омскийй государственный университет. 2003. – 110 с.

5. Манцев А.П. Математическая логика и теория алгоритмов. 2004. – 89 с.

6. Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов. М.: Академия. 2007. – 305 с.