
2. Операции над машинами Тьюринга.
Пусть
машины
 и
и
 имеют соответственно программы
имеют соответственно программы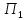 и
и .
Предположим, что внутренние алфавиты
этих машин не пересекаются и что
.
Предположим, что внутренние алфавиты
этих машин не пересекаются и что —
некоторое заключительное состояние
машины
—
некоторое заключительное состояние
машины ,
a
,
a
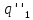 —
какое-либо начальное состояние машины
—
какое-либо начальное состояние машины Заменим
всюду в программе
Заменим
всюду в программе состояние
состояние на состояние
на состояние и
полученную программу объединим с
программой
и
полученную программу объединим с
программой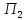 .
Новая программа П определяет машинуT,
называемую композицией
машин
.
Новая программа П определяет машинуT,
называемую композицией
машин
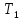 и
и
 (по паре состояний
(по паре состояний )
и обозначаемую через
)
и обозначаемую через или
или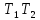
 более
подробно:
более
подробно: -
Внешний алфавит композиции
-
Внешний алфавит композиции
 является объединением внешних алфавитов
машин
является объединением внешних алфавитов
машин и
и
 .
.
Пусть
q'
— некоторое заключительное состояние
машины Г, а q"
— какое-либо состояние машины T,
не являющееся заключительным. Заменим
всюду в программе П машины T
символ q'
на q".
Получим
программу П',
определяющую машину T'(q',
q").
Машина T'
называется итерацией
машины
T
(по паре состояний

Пусть
машины Тьюринга
 ,
,
 и
и
 задаются программами
задаются программами ,
, и
и соответственно. Считаем, что внутренние
алфавиты этих машин попарно не
пересекаются. Пусть
соответственно. Считаем, что внутренние
алфавиты этих машин попарно не
пересекаются. Пусть и
и — какие-либо различные заключительные
состояния машины
— какие-либо различные заключительные
состояния машины .
Заменим всюду в программе
.
Заменим всюду в программе
 состояние
состояние некоторым начальным состоянием
некоторым начальным состоянием машины
машины ,
а состояние
,
а состояние
 некоторым начальным состоянием
некоторым начальным состоянием машины
машины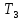 .
Затем новую программу объединим с
программами
.
Затем новую программу объединим с
программами и
и .
Получим программу П, задающую машину
Тьюринга
.
Получим программу П, задающую машину
Тьюринга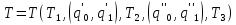 .
Эта
машина называется разветвлением
машин
.
Эта
машина называется разветвлением
машин
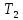 и
и
 ,управляемым
машиной
,управляемым
машиной
 .
.
При
задании сложных машин Тьюринга часто
применяют так называемую операторную
запись алгоритма,
которая представляет собой строку,
состоящую из символов, обозначающих
машины, символов перехода (вида
 и
и
 ),
а также символов α
и
ω,
служащих для обозначения соответственно
начала и окончания работы алгоритма. В
операторной записи (некоторого алгоритма)
выражение
),
а также символов α
и
ω,
служащих для обозначения соответственно
начала и окончания работы алгоритма. В
операторной записи (некоторого алгоритма)
выражение
 ,обозначает
разветвление машин
,обозначает
разветвление машин
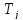 и
и
 ,
управляемое машиной
,
управляемое машиной ,
причем заключительное состояние
,
причем заключительное состояние машины
машины заменяется начальным состоянием
заменяется начальным состоянием машины
машины ,
а всякое другое заключительное состояние
машины
,
а всякое другое заключительное состояние
машины заменяется начальным состоянием машины
заменяется начальным состоянием машины (одним и тем же). Если машина
(одним и тем же). Если машина имеет одно заключительное состояние,
то символы
имеет одно заключительное состояние,
то символы и
и
 служат
для обозначения безусловного перехода.
Там, где не могут возникнуть недоразумения,
символы
служат
для обозначения безусловного перехода.
Там, где не могут возникнуть недоразумения,
символы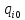 и
и опускаются.
опускаются.
Пример 3. Операторная схема

описывает
следующий «процесс вычисления». Начинает
работу машина
 .
Если она заканчивает работу в состоянии
.
Если она заканчивает работу в состоянии ,
то начинает работать машина
,
то начинает работать машина ,
а по окончании работы машины
,
а по окончании работы машины вновь «выполняет работу» машина
вновь «выполняет работу» машина .
Если же машина
.
Если же машина останавливается в некотором заключительном
состоянии, отличном от
останавливается в некотором заключительном
состоянии, отличном от то «работу продолжает» машина
то «работу продолжает» машина Если
Если приходит в заключительное состояние
приходит в заключительное состояние , то начинает работу машина
, то начинает работу машина ;
если же
;
если же заканчивает работу в некотором
заключительном состоянии, отличном от
заканчивает работу в некотором
заключительном состоянии, отличном от ,
то «работу продолжает» машина
,
то «работу продолжает» машина .
Если машина
.
Если машина когда-либо остановится, то процесс
вычисления на этом заканчивается.
когда-либо остановится, то процесс
вычисления на этом заканчивается.
3. Вычислимые функции.
Пусть
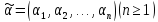 —
произвольный набор целых неотрицательных
чисел. Слово
—
произвольный набор целых неотрицательных
чисел. Слово
 называетсяосновным
машинным кодом
(или просто кодом)
набора
называетсяосновным
машинным кодом
(или просто кодом)
набора
 (в алфавите
(в алфавите )
и обозначается
)
и обозначается .
В частности, слово
.
В частности, слово
 является
основным машинным кодом числа
является
основным машинным кодом числа .
.
В
дальнейшем рассматриваются частичные
числовые функции. Функция
 называется частичной числовой функцией,
если переменные
называется частичной числовой функцией,
если переменные принимают значения из натурального
ряда с нулем:
принимают значения из натурального
ряда с нулем:
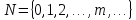 ,
и в том случае, когда на наборе
,
и в том случае, когда на наборе
 функция
функция определена,
определена, .
.
Частичная
числовая функция
 называетсявычислимой
(по
Тьюрингу),
если
существует машина Тьюринга
называетсявычислимой
(по
Тьюрингу),
если
существует машина Тьюринга
 ,
обладающая следующими свойствами:
,
обладающая следующими свойствами:
а) если
 определено,
то
определено,
то
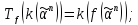
б) если
 не определено, то либо
не определено, то либо не является кодом никакого числа изN.
либо машина
не является кодом никакого числа изN.
либо машина
 не применима к слову
не применима к слову .
.
Замечание.
В дальнейшем предполагаем, что в начальный
момент головка машины обозревает самую
левую единицу слова
 .
Известно, что это ограничение не сужает
класса вычислимых функций.
.
Известно, что это ограничение не сужает
класса вычислимых функций.
Если
функция
 вычислима по Тьюрингу с помощью машины
вычислима по Тьюрингу с помощью машины ,
то будем говорить, чтомашина
,
то будем говорить, чтомашина
 вычисляет
функцию
вычисляет
функцию
 .
.
Говорят,
что машина Тьюринга Т
правильно вычисляет функцию
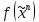 ,
если:
,
если:
а) в
случае, когда
 определено, машинаТ,
начав работу с левой единицы кода
определено, машинаТ,
начав работу с левой единицы кода
 ,
останавливается,
,
останавливается,
 и головка машины в заключительной
конфигурации обозревает левую единицу
кодаk(f(an));
и головка машины в заключительной
конфигурации обозревает левую единицу
кодаk(f(an));
б) в
случае, когда
 не определено, машинаТ,
начав работу с левой единицы кода
не определено, машинаТ,
начав работу с левой единицы кода
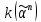 ,
не останавливается.
,
не останавливается.
Справедливо следующее утверждение: для всякой вычислимой функции существует машина Тьюринга, правильно вычисляющая эту функцию.
Расстояние
между двумя ячейками С и С'
ленты равно увеличенному на единицу
числу ячеек, расположенных между С
и С'.
В частности, соседние ячейки ленты
находятся друг от друга на расстоянии
1. Пусть l
— целое положительное число. Подмножество
всех таких ячеек ленты, каждые две из
которых расположены друг от друга на
расстоянии, кратном l,
называется решеткой
с шагом l.
Ленту
можно рассматривать как объединение l
решеток с шагом l.
Пусть
 — решетка с шагомl.
Две ячейки этой решетки называются
соседними,
если расстояние между ними, рассматриваемое
относительно всей ленты, равно l.
— решетка с шагомl.
Две ячейки этой решетки называются
соседними,
если расстояние между ними, рассматриваемое
относительно всей ленты, равно l.
Говорят,
что слово
 записано на решетке
записано на решетке
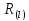 ,если:
,если:
символ
 записан в некоторой ячейке
записан в некоторой ячейке этой решетки;
этой решетки;
символ
 записан в ячейке
записан в ячейке ,
которая является соседней к
,
которая является соседней к на решетке
на решетке и расположена справа от нее и т.д.;
и расположена справа от нее и т.д.;
символ
 записан в ячейке
записан в ячейке ,
отстоящей от ячейки
,
отстоящей от ячейки
 на расстояние
на расстояние и расположенной справа от
и расположенной справа от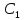 .
.
Будем
говорить, что машина
Тьюринга
 моделирует машину
Тьюринга
Т на решетке
моделирует машину
Тьюринга
Т на решетке
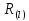 (с шагомl),
если, каково бы ни было слово Р
(в алфавите А),
выполняется следующее условие: пусть
на решетке
(с шагомl),
если, каково бы ни было слово Р
(в алфавите А),
выполняется следующее условие: пусть
на решетке
 записано словоР
и в начальный момент головка машины
записано словоР
и в начальный момент головка машины
 обозревает самую левую букву словаР;
машина
обозревает самую левую букву словаР;
машина
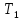 останавливается тогда и только тогда,
когда машинаТ
применима к слову Р;
при этом, если Т(Р)
определено, то после окончания работы
машины
останавливается тогда и только тогда,
когда машинаТ
применима к слову Р;
при этом, если Т(Р)
определено, то после окончания работы
машины
 на решетке
на решетке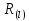 будет записано словоТ(Р).
будет записано словоТ(Р).
Справедливо
следующее утверждение: для
каждой машины Тьюринга Т и каждой
решетки
 с шагомl
можно построить машину Тьюринга
с шагомl
можно построить машину Тьюринга
 ,
моделирующую машину Тьюринга Т на
региетпке
,
моделирующую машину Тьюринга Т на
региетпке
Пусть
 —
произвольный набор целых неотрицательных
чисел; l-кратным
кодом этого набора
называется слово в алфавите {0, 1},
имеющее вид
—
произвольный набор целых неотрицательных
чисел; l-кратным
кодом этого набора
называется слово в алфавите {0, 1},
имеющее вид
 .
.
Справедливо
утверждение:
для
каждого фиксированного целого числа
n
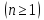 существует
машина Тьюринга, преобразующая основной
код любого набора
существует
машина Тьюринга, преобразующая основной
код любого набора
 в
его l-кратный
код, а также существует машина
Тьюринга, преобразующая l-кратный
код всякого набора
в
его l-кратный
код, а также существует машина
Тьюринга, преобразующая l-кратный
код всякого набора
 в
его основной код.
в
его основной код.
Решетчатым
кодом набора
 называется слово в алфавите {0, 1},
записанное на п
решетках с шагом п,
причем
так, что на первой решетке записано
слово
называется слово в алфавите {0, 1},
записанное на п
решетках с шагом п,
причем
так, что на первой решетке записано
слово
 ,
на второй — слово
,
на второй — слово и т.д., наn-й
— слово
и т.д., наn-й
— слово
 ;
начала слов на решетках должны бытьсогласованы,
т. е. самая левая единица на первой
решетке непосредственно предшествует
(на всей ленте) самой левой единице на
второй решетке, а эта единица непосредственно
предшествует самой левой единице на
третьей решетке и т. д.
;
начала слов на решетках должны бытьсогласованы,
т. е. самая левая единица на первой
решетке непосредственно предшествует
(на всей ленте) самой левой единице на
второй решетке, а эта единица непосредственно
предшествует самой левой единице на
третьей решетке и т. д.
Справедливо
утверждение:
для
всякого
фиксированного целого числа числа n
 можно
построить машину Тьюринга, преобразующую
основной код любого набора
можно
построить машину Тьюринга, преобразующую
основной код любого набора
 в
его решетчатый код, а также можно
построить машину Тьюринга, преобразующую
решетчатый код всякого набора
в
его решетчатый код, а также можно
построить машину Тьюринга, преобразующую
решетчатый код всякого набора
 в его основной код.
в его основной код.
Пример
4. Для функции
 построить машину Тьюринга, вычисляющую
ее, а также машину Тьюринга, правильно
вычисляющую эту функцию.
построить машину Тьюринга, вычисляющую
ее, а также машину Тьюринга, правильно
вычисляющую эту функцию.
Замечание.
Здесь и в дальнейшем при «аналитическом»
задании числовых функций используются
известные (из математического анализа)
«элементарные» функции. При этом
«аналитически» заданная функция
считается определенной только на таких
целочисленных наборах значений
переменных (принадлежащих множеству N
— натуральному ряду с нулем), на которых
определены и принимают целые неотрицательные
значения все «элементарные» функции,
входящие в рассматриваемое «формульное
задание» определяемой функции. Например,
функция
 определена лишь тогда, когда
определена лишь тогда, когда — целое неотрицательное число,
— целое неотрицательное число,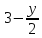 —
целое
положительное число и
—
целое
положительное число и
 —
целое неотрицательное число.
—
целое неотрицательное число.
Решение примера 4. Имеем

Нужно
построить такую машину Тьюринга Т,
которая «перерабатывает» любое слово
 в слово
в слово и удовлетворяет условию: либоТ(1)
не определено, либо Т(1)
не является основным машинным кодом
никакого числа из N.
и удовлетворяет условию: либоТ(1)
не определено, либо Т(1)
не является основным машинным кодом
никакого числа из N.
Попытаемся
реализовать следующую идею: стирая
самую левую единицу в слове
 и проходя оставшееся подслово
и проходя оставшееся подслово слева направо, головка пропускает еще
одну (пустую) ячейку («разделительный
нуль») и печатает две единицы подряд;
получается слово
слева направо, головка пропускает еще
одну (пустую) ячейку («разделительный
нуль») и печатает две единицы подряд;
получается слово ;
затем головка возвращается к левой
единице подслова
;
затем головка возвращается к левой
единице подслова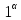 (если такая единица есть), вычеркивает
ее, проходит новое подслово
(если такая единица есть), вычеркивает
ее, проходит новое подслово слева
направо, потом проходит «разделительный
нуль» и две ранее напечатанные единицы
(справа от него), печатает еще две единицы
и опять возвращается к началу «остатка»
исходного слова
слева
направо, потом проходит «разделительный
нуль» и две ранее напечатанные единицы
(справа от него), печатает еще две единицы
и опять возвращается к началу «остатка»
исходного слова и
т.д.; когда в исходном слове все единицы
будут вычеркнуты, а во «вновь формируемом»
массиве все единицы будут напечатаны,
то на ленте «останется» массив из
и
т.д.; когда в исходном слове все единицы
будут вычеркнуты, а во «вновь формируемом»
массиве все единицы будут напечатаны,
то на ленте «останется» массив из единиц;
вычеркнем в нем две первые единицы и
«процесс вычисления» закончим.
единиц;
вычеркнем в нем две первые единицы и
«процесс вычисления» закончим.
Программа машины Тьюринга Т, реализующей описанную идею, выглядит так:







Имеем
 и
и (пустое
слово). Значит, машинаТ
действительно вычисляет заданную
функцию
(пустое
слово). Значит, машинаТ
действительно вычисляет заданную
функцию
 ,
но не является машиной Тьюринга, правильно
вычисляющей эту функцию (так как она
применима к слову 1, соответствующему
значению х
= 0, а на этом значении аргумента функция
,
но не является машиной Тьюринга, правильно
вычисляющей эту функцию (так как она
применима к слову 1, соответствующему
значению х
= 0, а на этом значении аргумента функция не определена). Чтобы из машиныТ
построить машину Т',
правильно вычисляющую функцию
не определена). Чтобы из машиныТ
построить машину Т',
правильно вычисляющую функцию
 достаточно удалить из программы машиныТ
команду q7~lqoOR
и добавить команды
достаточно удалить из программы машиныТ
команду q7~lqoOR
и добавить команды
 и
и .
.
