4. Проверочные расчёты валов
4.1 Расчёт вала на прочность
Основными нагрузками на валы являются силы от передач. Силы на валы передаются через насаженные на них детали: зубчатые или червячные колёса, звёздочки, шкивы, муфты. При расчёте принимают, что насаженные на вал детали передают силы и моменты на валу на середине своей ширины. Под действием постоянных по величине и направлению сил во вращающихся валах возникают напряжения, изменяющиеся по симметричному циклу.
Расчёт проводят в такой последовательности: по чертежу сборочной единицы вала составляют расчётную схему, на которую наносят все внешние силы, нагружающие вал, приводя плоскости их действия к двум взаимно перпендикулярным плоскостям (горизонтальной Х и вертикальной У). Затем определяют реакции опор в вертикальной и горизонтальной плоскости. В этих же плоскостях строят эпюры изгибающих и крутящих моментов, находят эквивалентный момент. Предположительно устанавливают опасные сечения, исходя из эпюр моментов, размеров сечений вала и концентраторов напряжений.
Расчетную схему нужно начинать с определения сил действующих на валы. В цилиндрических прямозубых передачах (Рис 4.1) силу в зацеплении раскладывают на две составляющие:
- Окружную Ft = 2T/d (4.1)
- Радиальную Fr = Ft · tgα (4.2)
где Т – вращающий момент, Н · м
d – диаметр делительной окружности, α – угол зацепления (обычно α=200).
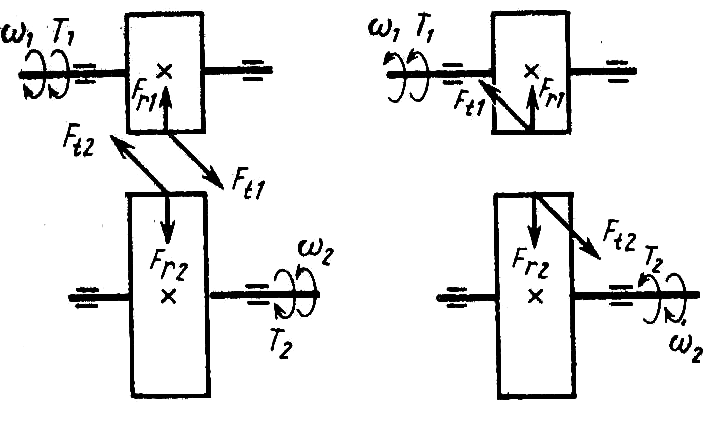
Рис 4.1. Схема сил в зацеплении прямозубой цилиндрической передачи
В цилиндрических косозубых передачах (Рис 4.2) силу в зацеплении раскладывают на три взаимно перпендикулярных составляющие:
- Окружную Ft = 2T/d
- Радиальную Fr = Ft · tgα/cosβ (4.3)
- Осевую Fa = Ft · tgβ (4.4)
где Т – вращающий момент, Н · м
d – диаметр делительной окружности
α – угол зацепления (обычно α=200);
β – угол наклона линии зуба.
Рис 4.2. Схема сил в зацеплении косозубой цилиндрической передачи
В конической прямозубой передаче
- Окружная сила Ft = 2T/d
- Радиальная сила на шестерне и осевая на колесе
Fr1 = Fа2 = Ft · tgα · sinδ2 (4.5)
Fa1 = Fr2 = Ft · tgα · sinδ1 (4.6)
Значение угла δ2 определяют по передаточному числу
tgδ2 = U = z2/z1 (4.7)
В передачах коническими колесами с косыми или круговыми зубьями (рис. 4.3)
Ft = 2T/d
(4.8)
(4.9)
здесь β – угол наклона линии зуба в середине ширины зубчатого венца. Знак перед вторым слагаемым выбирают в зависимости от направления вращения шестерни и наклона зубьев по таблице 10. Вращение по часовой стрелке или против определяется при взгляде на колесо от основания конуса к его вершине. Если осевое усилие Fa получилось со знаком «минус», то оно должно быть направлено к вершине конуса. Если Fa получилось со знаком «плюс», то оно должно быть направлено от точки контакта зубьев к центру шестерни. Сила Fa2 = Fr1, но направлена в противоположную сторону.
То же относится к Fr2 и Fa1.
Рис 4.3. Схема сил в зацеплении в конической передачи с круговым зубом и прямозубой
Таблица 10
Выбор знаков в формулах для определения Fr1 и Fa1
В червячной передаче (Рис 4.4)
Ft1 = Fа2 = 2T1/d1 (4.10)
Ft2 = Fа1 = 2T2/d2 (4.11)
Fr1 = Fr2 = Ft2 tgα (4.12)
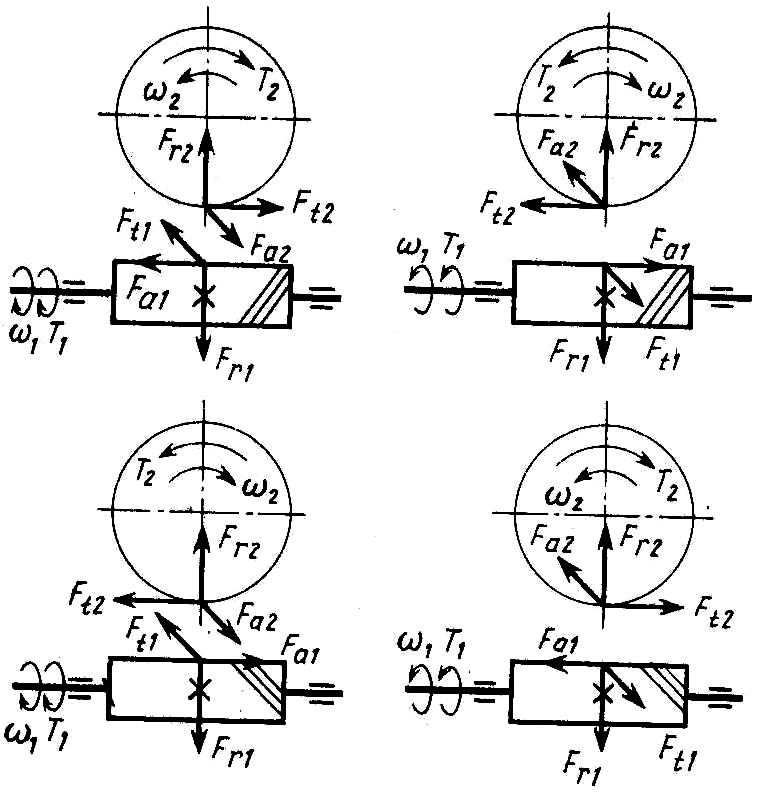
Рис 4.4. Схема сил зацепления в червячной передаче
Вычерчивается расчетная схема вала (Рис 4.5). При этом следует помнить, что радиальная и осевая силы лежат в одной плоскости (уOz), а окружная – в перпендикулярной к ней (xOz) плоскости.
Определяются опорные реакции в горизонтальной и вертикальной плоскости. Далее, общепринятым способом для определения опорных реакций в каждой плоскости составляется уравнение моментов относительно одной и другой опор. В заключении этого пункта обязательно должна быть проведена проверка полученных значений реакции по условию: в каждой плоскости сумма проекций всех сил на ось, перпендикулярную оси вала, должна равняться нулю. Если это условие не выполняется, то расчет не верен и его следует повторить. Возможна разница лишь в пределах погрешностей вычислений.
Известным способом строятся эпюры изгибающих моментов в обеих плоскостях Mx и My и вычерчиваются под соответствующими проекциями вала.
Путем анализа конструкции вала и эпюр изгибающих моментов намечаются несколько сечений, где будут большие изгибающие моменты или существенные коэффициенты концентрации напряжений. Для этих сечений определяются геометрические суммы изгибающих моментов в горизонтальной Mу и вертикальной Mч плоскостях:
(4.13)
Здесь же вычерчивается эпюра крутящего момента Т. Следует помнить, что одинаковый крутящий момент действует вдоль вала на длине между 2-мя насаженными на вал деталями
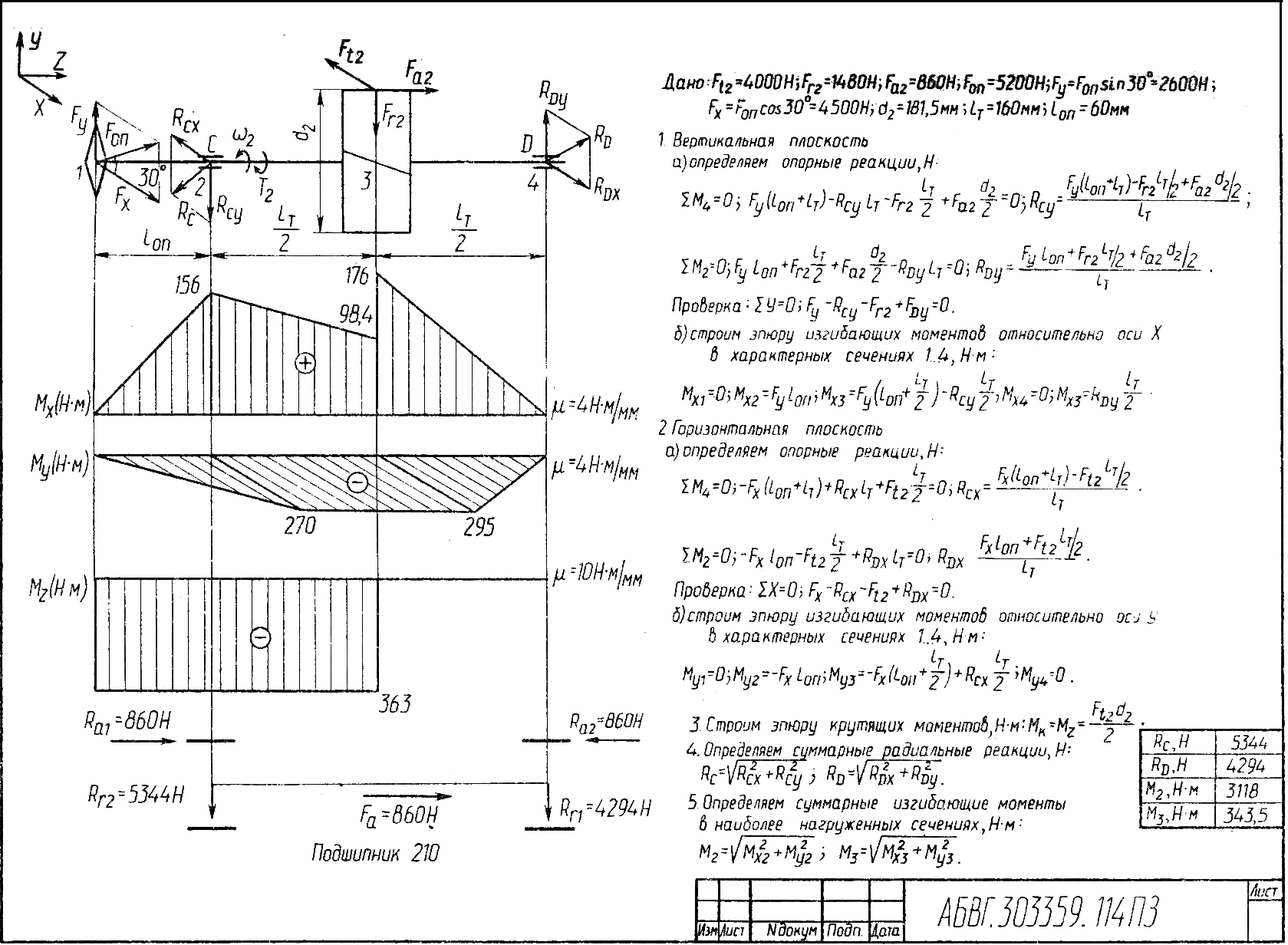
Рис 4.5. Пример расчетной схемы тихоходного вала цилиндрического одноступенчатого редуктора