6. Проверка подшипников.

Проверку подшипников производим на долговечность по динамической грузоподъемности, поскольку относительная частота внутреннего кольца больше 1 об/мин.

Известным способом [7,8] определяем потребную динамическую грузоподъемность и сравниваем ее с динамической грузоподъемностью выбранного подшипника для 1 и 2 опоры. При положительном результате проверки подшипников следует продолжить расчеты вала. В противном случае необходимо выбрать другие подшипники и выполнить корректировку длиновых размеров вала и предыдущих расчетов.

7. Построение эпюр изгибающих и крутящих моментов.

Вертикальная плоскость (рис.14)

Изгибающий момент на опоре 2

Нмм.

Изгибающий момент под усилием F_t

Нмм.

Эпюра построена на сжатом волокне.

Горизонтальная плоскость (рис.15)

Изгибающий момент под силой F_Rна сжатом волокне

Нмм.

Изгибающий момент под силой F_Rна растянутом волокне

Нмм.

Проверка: сумма двух моментов должна равняться моменту от осевой силы.

Нмм.

Нмм.

Результат проверки положительный.

Просуммируем изгибающие моменты вертикальной и горизонтальной плоскостей (рис.15):

в сечении A

Нмм;

Нмм;

в сечении B

Нмм.

8.Выявление опасных сечений.

Анализируя схему (рис.16), наметим наиболее опасные сечения, где будут действовать большие нагрузки и концентрации напряжений. Наметим три сечения:

всеченииAдействует максимальный изгибающий момент, крутящий момент, кроме того, ступица колеса установлена на шпонку и посадку с натягом, что создает концентрацию напряжений;

в сечении Bдействует большой изгибающий момент, крутящий момент, есть концентрация напряжений от посадки с натягом подшипника, но здесь меньше диаметр вала;

в сечении Cдействует крутящий момент, небольшой изгибающий момент, но при небольшом диаметре есть концентратор напряжений в виде галтели.

Поскольку сечение Cнаходится на промежуточном участке эпюры, определим дополнительно суммарное значение изгибающего момента в этом сечении. Из условия подобия треугольников

Нм.

9 Проверка вала на усталостную прочность по запасам прочности.

Выберем материал вала сталь 45 с улучшением. Для этой стали (табл.С1) при диаметре вала менее 100 мм предел прочности σ_В= 740 Мпа, предел текучести σ_Т= 440 Мпа. Тогда по формулам примечания к табл. С.1

Мпа;

Мпа.

Сечение A.

В этом сечении вала с диаметром d₄= 55 шпоночный паз имеет размеры

b= 16,t₁= 6, (таблица С.8)тогда моменты сопротивления сечения

мм³;

мм³.

Амплитуда и средние нормальные напряжения цикла

Мпа, .

Амплитуда и средние касательные напряжения цикла

Мпа.

Коэффициенты концентрации и масштабные факторы для шпоночного паза (таблицы С.2, С.3)

K_σ= 1,9;ε_σ= 0,77;K_σ/ε_σ= 1,9/0,77 = 2,5;

K_τ= 1,7;ε_τ= 0,85ε_σ= 0,85·0,77 = 0,65;K_τ/ε_τ= 1,7/0,65 = 2,6.

Коэффициенты концентрации и масштабные факторы для посадки с натягом (таблица С.6)

K_σ/ε_σ= 3,65;K_τ/ε_τ= 2,6.

Поскольку отношение коэффициентов концентрации для посадки с натягом выше, принимаем к расчету эти значения.

Коэффициент шероховатости для шлифованной поверхности β_П= 1 (таблица С.4) при отсутствии упрочнения.

Коэффициент чувствительности материала к асимметрии цикла напряжений для среднеуглеродистой стали (С7) Ψ_σ= 0,1; Ψ_τ= 0,05.

Тогда запас прочности по нормальным напряжениям

.

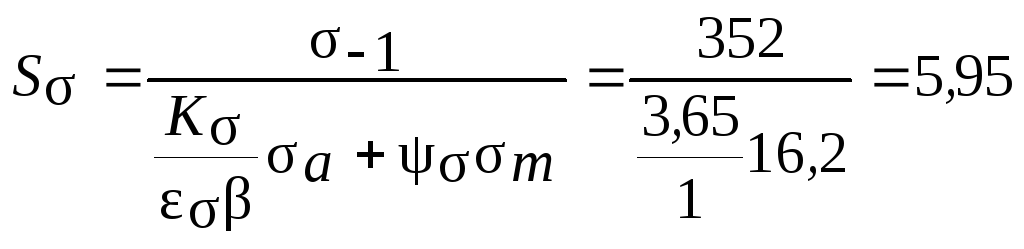Запас прочности по касательным напряжениям

.

Суммарный запас усталостной прочности в сечении A

.

Сечение B.

В этом сечении вал имеет диаметр d₃= 50 и посадку с натягом.

Моменты сопротивления

мм³;

мм³.

Амплитуда и средние нормальные напряжения цикла

Мпа; .

Амплитуда и средние касательные напряжения цикла

Мпа.

Коэффициенты концентрации и масштабные факторы для посадки с натягом (таблица С.6)

K_σ/ε_σ= 3,65;K_τ/ε_τ= 2,6.

Коэффициент шероховатости для шлифованной поверхности β_П= 1 (таблица С.4) при отсутствии упрочнения.

Коэффициент чувствительности материала к асимметрии цикла напряжений для среднеуглеродистой стали (С7) Ψ_σ= 0,1; Ψ_τ= 0,05.

Тогда запас прочности по нормальным напряжениям

;

Запас прочности по касательным напряжениям

.

Суммарный запас усталостной прочности в сечении B

.

Сечение C.

В этом сечении вал имеет диаметр d₃= 40 и концентратор в виде галтели с радиусомr= 2.

Моменты сопротивления

мм³;

мм³.

Амплитуда и средние нормальные напряжения цикла

Мпа; .

Амплитуда и средние касательные напряжения цикла

Мпа.

Коэффициенты концентрации по галтели и масштабные факторы (таблица С.2).

При d₂/d₁= 45/40 = 1,13 иr/d₁= 2/40 = 0,05

K_σ= 1,53;ε_σ= 0,81;K_σ/ε_σ= 1,53/0,81 = 1,89;

K_τ= 1,19;ε_τ= 0,85ε_σ= 0,85·0,81 = 0,69;K_τ/ε_τ= 1,19/0,69 = 1,72.

Коэффициент шероховатости для шлифованной поверхности β_П= 1 (таблица С.4) при отсутствии упрочнения.

Коэффициент чувствительности материала к асимметрии цикла напряжений для среднеуглеродистой стали (С7) Ψ_σ= 0,1; Ψ_τ= 0,05.

Тогда запас прочности по нормальным напряжениям

;

Запас прочности по касательным напряжениям

.

Суммарный запас усталостной прочности в сечении B

.

В одном из выбранных опасных сечениях, в сечении B, запас прочностиS_B= 4,41укладывается в допускаемые пределы

S= 1,5…5,0.