книги / Теплофизические явления в полимерных материалах при интенсивном и кратковременном воздействии

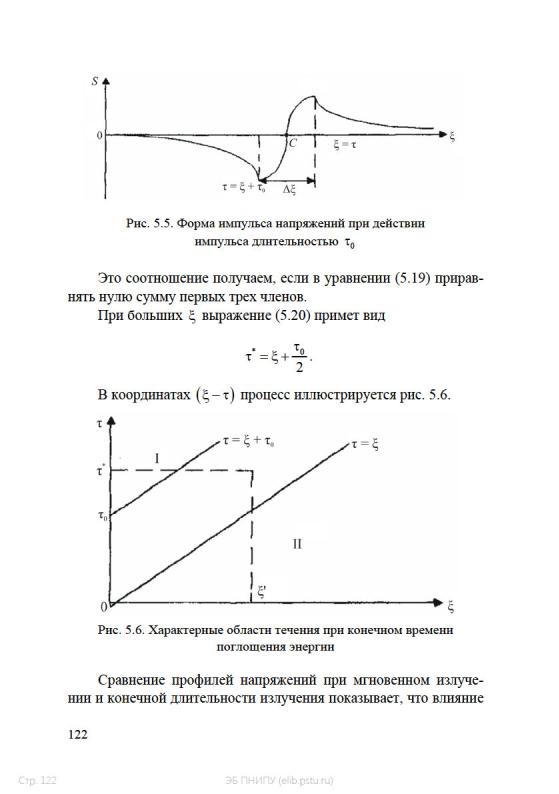
длительности излучения приводит к образованию зоны конечной

Зависимость Smax+ от длительности излучения τ0 показана на рис. 5.7 для больших значений ξ.

Рис. 5.7. Зависимость Smax (τ0 )

Зависимости Smax+ и Smax− от τ0 для заданной функции ϕ(τ)

одинаковы.

Приведем результаты численного расчета по формуле (5.21):

Как следует из этих данных, максимальные напряжения, как сжимающие так и растягивающие, в сильной степени зависят от параметра длительности излученияτ0 . Экспериментально резкое снижение максимальной амплитуды волны сжатия с возрастанием τ0 зарегистрировано на мишени из алюминия. При увеличении τ0 с 5 до 50 нс амплитуда уменьшилась в τ0 ≈ 8 раз.

Из уравнения (5.19) при τ= τ0 + ξ получаем:

При больших ξ

124

ближаются к своим значениям, равным 0,5, для мгновенного излучения. Следовательно, значение τ0 может служить критерием режима разогрева вещества при поглощении в нем энергии излучения. При значении τ0 <1 режим разогрева близок к мгновенному. Напротив, если τ0 ≥ 1, то режим разогрева можно считать

медленным.

Выясним физический смысл введения безразмерного времени разогрева τ0 = µ C0 t0 , где t0 – конечная длительность излу-

чения. По определению, µ = 1l0 ,где l0 – длина свободного про-

бега излучения, которую можно принять за характерную ширину прогревной зоны.

ны, охваченной возмущением (волной разгрузки). Таким образом, если τ0 <1, то C0 t0 < l0 , т.е. ширина прогревной зоны превосхо-

дит ширину зоны, охватываемой волной расширения, и волна расширения не успевает снять давления, создаваемые нагревом.

Напротив, если τ0 >1, то C0 t0 > l0 , волна разгрузки снимает

давления, создаваемые в зоне прогрева, и в ней реализуются меньшие давления.

Заметим, что в действительности детали из полимерных высокоэнергетических материалов имеют ограниченные размеры и, как правило, цилиндрическую конфигурацию с радиусом R0. В таком случае рассмотренное выше приближение верно, если l0 << R0 .

симальные положительные давления достигаются на характеристике τ0 = ξ, т.е. максимум движется вправо со скоростью звука С0 и изменяется с координатой ξ по закону:

динатой ξ = τ0 , а затем начинает уменьшаться, стремясь к посто-

янной величине S∞ = 12 (1−e−τ0 ). Максимальные растягивающие

напряжения реализуются на характеристике τ = ξ+ τ0 . Их амплитуда монотонно возрастает по закону:

экспоненциально приближаясь к S∞.

Исследуем зависимость амплитуды импульсов сжатия и растяжения от длительности воздействия излучения τ0 .

максимума давления смещается к облучаемой поверхности и его амплитуда линейно уменьшается с сокращением длительности импульса.

При движении вглубь материала амплитуда импульса сжатия уменьшается вдвое по сравнению со своим максимальным значением [138]. Приближение малых τ0 справедливо при τ0 <1.

Если же τ0 >1, то амплитуда давления, как это видно из (5.22),

126

практически не зависит от τ0 и равна своему максимальному значению 0,5 при ξ > τ0 . Это означает, что увеличение времени воздействия на материал существенно влияет на амплитуду волн сжатия: Smax+ ≈ τ0 до тех пор, пока τ0 не достигнет критического

значения µ 1C0 . Дальнейшее увеличение длительности импульса

практически не приводит к заметному увеличению амплитуды волн. Аналогичный вывод [139] следует и для растягивающих напряжений из анализа (5.23).

Рассмотрим другой случай, когда поглощенная энергия по-

стоянна: Q = ε0 µτC0 0 .

В этом случае при изменении длительности воздействия излучения поверхностная плотность поглощенной энергии остается постоянной. При τ0 → 0 максимум давления смещается к облучаемой поверхности и увеличивается по амплитуде, стремясь к значению µγГQ . По мере распространения вглубь материала

амплитуда уменьшается в два раза по сравнению со своим максимальным значением. Увеличение времени излучения приводит к уменьшению Smax+ . В отличие от предыдущей ситуации изменение длительности излучения слабо влияет на амплитуду волн

приводит к уменьшению амплитуды: Smax+ ≈ τ1 .

0

В целом данная модель пригодна для описания термоупругих напряжений, возникающих в деталях из полимерных высокоэнергетических материалов при облучении их СВЧ-излучением. Отметим лишь, что при использовании полученных соотношений необходимо учитывать область их применимости:

127

1)концентрация энергии излучения должна быть меньше теплоты испарения материала;

2)во-вторых, охлаждение поглощающего слоя за счет теплопроводности за время действия импульса должно быть малым.

Последнее условие можно представить в виде

τ0 << χc0µ3 ,

где χ – коэффициент температуропроводности.

Итак, при рассмотрении процессов воздействия сверхвысокочастотного излучения на полимерные материалы были получены качественные и количественные характеристики напряжений при мгновенном поглощении энергии монохроматического электромагнитного излучения. Сравнивая профили напряжений при мгновенном излучении и конечной длительности излучения, видим, что влияние длительности излучения приводит к образованию зоны конечной длины, в которой напряжение меняется от максимального положительного до максимального отрицательного значения.

Несмотря на простоту, рассмотренная модель качественно и количественно пригодна для описания термоупругих напряжений, возникающих в деталях из полимерных высокоэнергетических материалов при облучении их сверхвысокочастотным излучением. Рассмотренные схемы течений являются основополагающими либо для описания разрушений, либо для описания колебаний в материалах, подвергнувшихся импульсному облучению.

5.4. Механические эффекты в деталях из полимерных высокоэнергетических материалов при тепловом ударе

Воздействие на материал кратковременных импульсов излучения приводит к импульсному разогреву материала. Такое явление носит название теплового удара [138].

128

Быстрый и неравномерный разогрев заряда твердого топлива создает в последнем волны напряжений. В области, примыкающей к свободной поверхности, внутри заряда формируется импульс сжимающих напряжений, который начинает движение в направлении свободной поверхности. Ввиду инерционности материала и наличия градиента напряжения сплошная среда приходит в движение.

На свободной поверхности давление равно атмосферному, т.е. можно считать, что оно равно нулю. Поэтому считают, что внутрь заряда снаружи движется виртуальный импульс (такой же по форме, что и импульс сжатия) растягивающих напряжений. При определенных условиях растягивающие напряжения могут вызвать разрушение заряда путем откола. Если откол не реализуется, то в результате циркуляции волн движение заряда приобретает колебательный характер.

Рассмотренные процессы относятся к случаю, если концентрация поглощенной энергии не превосходит энергии связи материала.

В подразд. 5.2 и 5.3 для однородного случая получены решения для волн напряжений S сжатия и растяжения как функций времени t и координаты х. При мгновенном выделении и поглощении энергии падающего излучения это решение S1 по (5.16), при конечном времени t0 облучения заряда и поглощении последним энергии этого излучения это решение S2 по (5.19).

Здесь, как и прежде, приняты следующие безразмерные функции координаты и параметры:

−безразмерное время τ =µ C0 t;

−безразмерное время облучения τ0 =µ C0 t0 .

Вформулах (5.24), кроме вышеназванных трех параметров σ, t

иx, использованыследующиеразмерныепараметрысостояния:

129

µ – линейный коэффициент поглощения энергии; γГ – коэффициент Грюнайзена;

E0 – энергия, падающая на единицу площади поверхности

Дж заряда, м2 ;

C0 – скорость звука вматериале заряда вначальном состоянии. Также использована единичная функция Хэвисайда h(z):

h(z)=1 при z ≥ 0,

h(z)= 0 при z < 0.

В качестве объекта исследования выбрана деталь диаметром 1 м. Выбраны типичные значения параметров состава: плотность

вующего СВЧ-излучения выбраны следующие: время излучения

где Z0 – волновое сопротивление материала заряда, Ом,

Z0 = 120επ.

По этим данным рассчитаны волновые картины для шести моментов времени, в которые фронт волны растяжения достигает координат: 0; 0,1; 0,2; 0,3; 0,4; 0,5 м. На рис. 5.8 изображены данные расчета (номера кривых соответствуют моментам времени,

мкс: 0–0; 1–34; 2–68; 3–102; 4–136; 5–171).

130