
книги / Нелинейная оптика
..pdf
вращающая сила F уже не описываются формулами (для одномерного движения rr = х):
U = |
1 |
kx2 |
, F = −kx. |
(2.11) |
|
2 |
|||||
|
|
|
|
Рассмотрим общую модель ангармонического осциллятора без затухания. Для адекватного описания осциллятора при высоких
интенсивностях света в разложении в ряд функции U (x) следует учесть члены более высоких степеней (ангармонические члены):
U (x)= |
1 |
kx2 |
− |
1 |
mеβx3 |
− |
1 |
mеδ x4 |
+ . |
(2.12) |
|
2 |
3 |
4 |
|||||||||
|
|
|
|
|
|
|
|
С учетом формулы Fr = − U это приводит к зависимости:
F (x)= −kx + mеβx2 + mеδ x3 + , |
(2.13) |
и, в отсутствие затухания, соответственно, к уравнению динамики:
d 2 x |
2 |
|
e |
|
2 |
|
3 |
|
|
|
dt |
2 |
+ω0 x = |
|
E (t)+βx |
|
+ δx |
|
+ . |
(2.14) |
|
|
|
|
||||||||
|
|
mе |
|
|
|
|
|
|||
В формулах (2.11)–(2.14) х – смещение от положения равновесия, mе − масса электрона, k – коэффициент квазиупругой силы, β и
δ – «упругие» константы молекулы, зависящие от ее химической природы, ω0 = k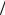 mе – собственная частота гармонических колебаний осциллятора для случая, когда интенсивность света мала. Принимая, что поправки βx2 и δx3 невелики, решение (2.14) можно
mе – собственная частота гармонических колебаний осциллятора для случая, когда интенсивность света мала. Принимая, что поправки βx2 и δx3 невелики, решение (2.14) можно
найти методом последовательных приближений.
В нулевом приближении ангармонические члены отбрасываются, и нулевое решение имеет вид:
x |
(t )= |
(e Eт |
mе ) cosωt |
, |
(2.15) |
||
ω2 |
−ω2 |
||||||
0 |
|
|
|
||||
|
|
|
0 |
|
|
|
|
41

что дает Р = N0ex0 (t )= ε0χ(1) Е(t), и линейная восприимчивость для одиночного осциллятора вычисляется следующим образом:
α(1) (ω)= |
1 |
χ(1) (ω) = |
e2 |
|
|
|
1 |
. |
(2.16) |
||
N |
0 |
ε m |
ω2 |
−ω2 |
|||||||
|
|
|
|
|
|||||||
|
|
|
0 |
е |
|
0 |
|
|
|
||
Последняя формула получается из (2.6), если положить β0 = 0.
В первом приближении следует подставить решение нулевого приближения (2.15) в уравнение (2.14), которое теперь, с учетом того, что:
cos2 ωt = |
|
1 |
(1+ cos 2ωt ), |
cos3 ωt = |
3 |
cos ωt |
||||||
2 |
|
|||||||||||
|
|
|
|
|
|
|
4 |
|
|
|||
примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 x |
|
2 |
|
eEт |
|
|
β(eEт mе )2 |
(1+ |
|||
|
|
+ω0 x = |
|
cosωt |
+ |
|
||||||
|
dt2 |
mе |
2(ω02 −ω2 )2 |
|||||||||
+δ(eEт 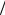 mе )3 (3cosωt + cos(3ωt )).
mе )3 (3cosωt + cos(3ωt )).
4(ω02 −ω2 )3
+ 14 cos3ωt,
cos 2ωt )+
(2.17)
В уравнении (2.17) вынуждающая сила представлена тремя гармоническими членами с частотами ω, 2ω, 3ω и одним статическим слагаемым. Поэтому частное решение (2.17) представляется как суперпозиция решений на частотах 0, ω, 2ω, 3ω.
Заметим, что для статической составляющей уравнение динамики имеет вид:
|
|
|
|
d 2 x |
2 |
β(eEт mе )2 |
|
|
|
|
|
|
|
+ω0 x = |
|
. |
(2.18) |
|
|
|
|
dt2 |
2(ω02 −ω2 )2 |
|||
Поскольку |
d 2 x |
= 0, то |
|
|
|
|
||
dt |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
42

|
|
|
|
|
|
|
x = |
|
β |
(eEт mе )2 |
|
|
|
1 |
|
. |
|
|
|
(2.19) |
|||||||
|
|
|
|
|
|
|
|
|
|
(ω02 −ω2 )2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
стат |
|
2 |
|
|
|
ω02 |
|
|
|
|
|
|
||||||||
Таким образом, установившиеся вынужденные колебания в |
|||||||||||||||||||||||||||
первом приближении описываются уравнением вида: |
|
|
|||||||||||||||||||||||||
x(t )= |
(e mе )Eт cosωt |
|
+ |
|
β(eEт mе )2 |
|
|
|
1 |
+ |
cos 2ωt |
|
+ |
||||||||||||||
(ω02 |
−ω2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
( |
|
) |
2 |
|
ω02 |
ω2 −(2ω)2 |
|||||||||||||||||||
|
|
|
|
|
|
ω2 −ω2 |
|
|
|
|
(2.20) |
||||||||||||||||
|
δ(eEт mе ) |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
||||||||
+ |
|
3cosωt |
+ |
|
cos3ωt |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||
( 0 |
−ω2 |
) |
3 |
|
ω02 −ω2 |
|
0 |
−(3ω)2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ω2 |
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
Поскольку колебания оптического электрона кроме основной частоты совершаются на удвоенной и утроенной частотах, то в оптической среде под действием падающей волны возникают дополнительные волны с частотами 2ω и 3ω, что означает нарушение одного из основных принципов линейной оптики о неизменности частоты света при переходе из одной среды в другую. Вторая гармоника (2ω) может возбуждаться в прозрачной среде даже при не-
большом ангармонизме оптических электронов. Кроме того, в согласии с (2.20), кубичная ангармоничность (δx3 ) вызывает измене-
ние поляризованости на основной частоте.
Действительно, объединяя члены с частотой ω, получаем:
x1 (t )= |
(eE |
т |
m )cosωt |
|
δ |
|
eE |
m |
3 |
3cos |
ωt |
|
||||
|
|
|
е |
|
+ |
|
|
|
т е |
|
|
|
; |
|||
|
|
|
ω02 −ω2 |
|
4 |
(ω02 |
|
ω02 −ω2 |
||||||||
|
|
|
|
|
|
|
|
−ω2 ) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 (t )= |
ε0 χ(ω)Eт cos ωt , |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
и так как χ(ω) = |
|
e |
|
|
|
x1 (t ) |
, то: |
|
|
|
|
|
|
|
|
|
ε0 |
Eт cos ωt |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
43
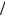
|
χ(ω) = χ(1) (ω) + χ(3) (ω)Eт2 , |
|
(2.21) |
||||||
где χ(1)(ω) вычисляется по формуле (2.16), а |
|
|
|||||||
χ |
(3) |
(ω) = |
3 |
χ |
(1) |
(ω)δ |
(e mе )2 |
. |
(2.22) |
|
4 |
|
(ω02 −ω2 )3 |
||||||
|
|
|
|
|
|
|
|
||
Формула (2.21) показывает зависимость поляризованности среды, а значит и показателя преломления, от интенсивности па-
дающей волны (Iпад ~ Em2 ). Таким образом, вследствие кубичной
ангармоничности (член δх3 в уравнении (2.14)) световое поле оказывает влияние на характер отклика среды, который становится нелинейным.
При моделировании среды ангармоническими осцилляторами возвращающая сила отвечает нелинейному закону Гука (сила не пропорциональна растяжению «пружины», а содержит нелинейную составляющую). Считая нелинейность слабой, запишем для изотропной среды одномерное волновое уравнение (1.26) с учетом затухания в виде:
d 2 P |
|
|
dP |
2 |
|
|
2 |
|
|
|
3 |
|
2 |
|
|
+ 2β |
|
|
+ω P + K |
|
P |
|
+ K |
|
P |
|
+... = ε |
ω |
E. (2.23) |
dt2 |
0 dt |
|
|
|
|
|||||||||
|
0 |
2 |
|
|
|
3 |
|
|
0 |
p |
|
|||
Условие слабой нелинейности означает выполнение неравенств:
ω02 >> |К2·Р|, ω02 >> |К3·Р2|. |
(2.24) |
Рассмотрим модель ангармонического осциллятора с квадра-
тичной нелинейностью (К3 = 0) для нерезонансного случая. Уравнение (2.23) принимает вид:
d 2 P |
|
|
dP |
2 |
|
|
2 |
|
2 |
|
|
|
+ 2β |
|
|
+ω P + K |
|
P |
|
= ε |
ω |
E. |
(2.25) |
dt2 |
0 dt |
|
|
||||||||
|
0 |
2 |
|
|
0 |
p |
|
|
|||
44
Нерезонансный случай означает, что комбинации частот поля не близки к частоте собственных колебаний ω0 . При этом рассмотре-
ние справедливо только для не слишком больших времен. Моделью среды может служить кристалл с постоянной решетки a. Тогда коэффициент квадратичной нелинейности оценивается следующим
ω02 .
еа
Решим уравнение (2.25) методом малых возмущений. Введем малый параметр ξ и представим уравнение (2.25) в виде:
|
d 2 P |
|
|
dP |
2 |
|
|
2 |
|
2 |
|
|
|
|
|
+ 2β |
|
|
+ ω P + K |
|
P |
|
= ξ ε |
ω |
p |
E. |
(2.26) |
|
dt2 |
0 dt |
|
|
|||||||||
|
|
0 |
2 |
|
|
0 |
|
|
|
||||
Ищем решение в виде ряда по малому параметру ξ: |
|
|
|
||||||||||
|
|
Р = ξ·Р(1) + ξ2·Р(2) + ξ3·Р(3) + … |
|
|
|
(2.27) |
|||||||
Подставив (2.27) в (2.26) и собрав члены порядка ξ, ξ2, ξ3, …, получим цепочку линейных неоднородных уравнений:
|
|
|
|
|
|
d 2 P(1) |
|
|
|
|
|
|
dP(1) |
|
2 |
P |
(1) |
|
|
|
2 |
E, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
2β |
|
|
|
|
+ ω |
|
= ε |
ω |
|
|
|
|
||||||||||
|
|
|
|
|
|
dt2 |
0 dt |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
p |
|
|
|
|
|
|
||||||||||
|
|
|
|
d 2 P(2) |
|
+ 2β |
|
|
dP(2) |
+ω2 |
P(2) = −К |
|
|
Р(1) |
2 |
, |
||||||||||||||||||
|
|
|
|
|
dt2 |
|
|
|
dt |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
d 2 P(3) |
|
|
|
|
|
|
dP(3) |
|
2 |
|
(3) |
|
|
|
|
|
|
(1) |
|
|
(2) |
|
|||||||||
|
|
|
|
|
|
|
|
+ 2β |
|
|
|
|
|
|
|
+ω P |
|
= −2К |
|
Р |
|
Р |
|
|
, |
|||||||||
|
|
|
|
|
dt2 |
|
|
|
dt |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…… |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d |
2 |
(m) |
|
dP |
(m) |
|
|
|
|
|
|
|
|
|
m−1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
P |
+ 2β0 |
|
|
|
|
+ω02 P(m) = − |
К2 ∑P(l ) P(m−l ) ,m ≥ 2. |
||||||||||||||||||||||||||
|
|
2 |
dt |
|
|
|
||||||||||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l =1 |
|
|
|
|
|
|
|
|
|
|||||||||
(2.28)
(2.29)
(2.30)
(2.31)
Систему (2.28)–(2.31) слеёдует решать последовательно, начиная с (2.28). Уравнение (2.28) совпадает с фигурирующим в линейной модели Друде – Лоренца уравнением (2.3), и его решение при-
45
водит к выражению для (линейного) показателя преломления среды, вытекающему из (2.7) при β0 = 0. Правая часть уравнения m-го порядка (2.31) определяется через найденные ранее величины (в более низких порядках теории возмущений).
Применим общие соотношения к случаю бигармонического воз-
буждения осциллятора с квадратичной нелинейностью, т.е. случаю воздействия двух внешних волн с частотами соответственно ω1 и ω2.
Описанная выше процедура решения системы уравнений (2.28)–(2.31) приводит к следующим выражениям для квадратичных восприимчивостей:
|
|
|
|
1 |
|
|
|
|
|
χ(1) (ω) |
2 |
|
||
χ(2) (2ω;ω,ω) = − |
К |
2 |
|
|
|
, |
|
|||||||
2 |
|
D(2ω) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
χ(2) (ω + ω ;ω ,ω ) = −К |
|
|
χ(1) (ω )χ(1) (ω ) |
, |
||||||||||
2 |
1 |
2 |
||||||||||||
1 |
2 |
1 |
2 |
|
|
|
|
D(ω1 + ω2 ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.32) |
χ(2) (ω −ω ;ω ,ω ) = −К |
|
|
χ(1) (ω )χ(1) (ω ) |
, |
||||||||||
2 |
|
1 |
2 |
|||||||||||
1 |
2 |
1 |
2 |
|
|
|
|
D(ω1 −ω2 ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
χ(1) (ω) |
2 |
|
||
χ(2) (0;ω,−ω) = − |
К |
2 |
|
|
|
. |
|
|||||||
2 |
|
D(0) |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
В этих коэффициентах квадратичной восприимчивости первый аргумент в скобках – частота колебаний поляризованности, а два последующих – частоты колебаний оптических полей (со знаками «+» или «–»). Функция D(ω) имеет вид:
D(ω) = ω02 – ω2 – i·2β0ω,
а знак «*» означает комплексное сопряжение.
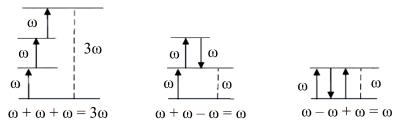
Соотношение частот колебаний поляризованности среды (штриховые вертикальные линии) и внешних световых полей (сплошные вертикальные линии) иллюстрирует рис. 6, где знаки «+» и «–» отвечают противоположным вертикальным направлениям (соответственно «вверх» и «вниз»).
46
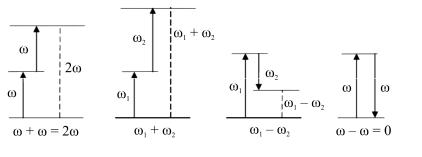
Рис. 6, а отвечает первой формуле (2.32), т.е. генерации в среде второй гармоники по отношению к исходной частоте оптического излучения. На рис. 6, б и 6, в иллюстрируется, соответственно, генерация в данной среде суммарной и разностной частот. Наконец, рис. 6, г отвечает «оптическому выпрямлению» – генерации в среде электростатического поля под действием оптического излучения.
Рис. 6, а можно получить из рис. 6, б, а рис. 6, г – из рис. 6, в в пределе совпадающих частот. Наглядно рис. 6 (и последующий рис. 7) можно интерпретировать на квантовом языке как генерацию в среде фотонов с суммарными илиразностными частотами.
Таким образом, в задаче о бигармоническом возбуждении осциллятора с квадратичной нелинейностью в приближении низшего порядка появляются:
•отклики с частотами вторых гармоник 2ω1 и 2ω2;
•отклик с нулевой частотой, соответствующий «выпрямле-
нию» света за счет квадратичной нелинейности βx2 ;
• отклики с суммарной и разностной частотами ω1 + ω2 и ω1 – ω2, соответствующие биениям между двумя световыми волнами.
а |
|
б |
|
в |
|
г |
|
|
|
|
|
|
|
Рис. 6. Соотношение частот колебаний квадратичной поляризованности среды и оптических полей
47
Связь (2.32) между линейными и квадратичными восприимчивостями может быть представлена в виде:
χ(2) (ω ± ω ;ω ,ω ) |
|
|
= − |
1 |
|
К |
2 |
. |
|||
1 2 |
1 2 |
|
|
|
|
|
|||||
χ(1) (ω ± ω ) χ(1) |
(ω ) χ(1) |
(ω |
) |
2 |
ε |
ω2 |
|||||
|
|
|
|||||||||
1 2 |
1 |
2 |
|
|
|
|
0 |
|
р |
|
|
Существенно, что правая часть в последнем выражении не зависит от частоты. Поскольку для различных оптических сред значения плазменной частоты ωр и коэффициента ангармонизма К2 варьируются не сильно, это позволяет сформулировать так называемое пра-
вило Р. Миллера:
χ(2) (ω ± ω ;ω ,ω ) |
(ω ) ≈ const. |
(2.33) |
|||||
χ(1) (ω ± ω ) χ(1) |
(ω ) χ(1) |
||||||
|
1 |
2 |
1 |
2 |
|
|
|
1 |
2 |
|
1 |
|
2 |
|
|
Физический смысл правила Р. Миллера (2.33) состоит в том, что квадратичная восприимчивость для различных соотношений частот колебаний поляризованности среды и оптических полей прямо пропорциональна произведению линейных восприимчивостей для соответствующих частот.
Из соотношения (2.33) вытекает простая и наглядная связь между величиной квадратичной восприимчивости χ(2) и коэффициен-
том преломления n:
χ(2) = αn3,
где α – некоторый множитель, практически постоянный для широкого класса нелинейных материалов. Согласно этому, квадратичная восприимчивость вещества тем выше, чем больше показатель пре-
ломления (аналогом этого результата для линейной восприимчивости является уравнение (2.8)).
Как и для линейной восприимчивости, полюса (нули знаменателей) квадратичных восприимчивостей (2.32) лежат в нижней полуплоскости комплексной плоскости частот.
Согласно (2.31), в следующем (третьем) порядке теории возмущений поляризованность имеет кубическую зависимость по ам-
48
плитудам излучения. Спектр ее осцилляций включает вторую и третью гармоники, а также частоты, совпадающие с исходными частотами излучения.
Рассмотрим модель ангармонического осциллятора с кубичной нелинейностью (К2 = 0). Если «восстанавливающая сила» меняет знак при изменении знака отклонения осциллятора (соответственно, потенциал – четная функция отклонения), то члены с четными степенями в (2.23) отсутствуют и низшим нелинейным членом служит кубический. Соответственно, при слабой нелинейности и монохроматическом внешнем излучении с частотой ω уравнение (2.23) можно записать в форме:
d 2 P |
|
|
|
dP |
2 |
|
|
3 |
|
2 |
|
|
|
|
|
+ 2β |
|
|
|
+ ω P + K |
|
P |
|
= ε |
ω |
E |
|
cosωt. |
(2.34) |
dt2 |
|
dt |
|
|
|
|||||||||
|
0 |
|
0 |
3 |
|
|
0 |
p |
|
т |
|
|
Это уравнение носит название уравнения Дуффинга. Хотя его точное решение отсутствует, разработаны эффективные методы его приближенного решения.
Как и в рассмотренном выше случае квадратичной нелинейности, можно воспользоваться нерезонансным приближением. Находя приближенное решение уравнения Дуффинга, получаем следующие качественные результаты: при монохроматическом возбуждении рис. 6 заменяется на схемы для модели с кубичной нелинейностью
(см. рис. 7).
Рис. 7. Соотношение частот колебаний кубичной поляризованности среды и внешнего поля
49

Рис. 7, а отвечает уже известной нам генерации гармоники, на этот раз третьей. Новыми свойствами обладает иллюстрируемый рис. 7, б и 7, в механизм нелинейности – для него частота колебаний поляризованности совпадает с частотой возбуждающего излучения. Этот тип нелинейности отвечает самовоздействию; можно убедиться (см. главу 3), что он может быть описан в терминах нелинейного (зависящего от интенсивности) показателя преломления.
Детальный расчет показывает, что между нелинейными поляризованностями смежных порядков Р(n) и P(n+1) в рамках модели ангармонического осциллятора может быть получено следующее соотношение:
P(n+1) |
|
≈ |
e |
|
E |
|
β |
, |
(2.35) |
|
|
|
|||||||
|
|
|
|
|
|
|
|||
P(n) |
m D2 |
|
(ω) |
||||||
|
|
|
e |
|
|
|
|
||
где β – коэффициент ангармоничности из уравнения (2.14). На основе рассмотрения физической природы связи электрона в атоме можно считать, что если отклонение х по порядку величины равно радиусу rа равновесной орбиты электрона, то нелинейная сила теβх2 имеет величину того же порядка, что и линейная сила теω02 rа = = е|Еат|, где Еат – напряженность внутриатомного электрического поля, связывающего электрон. Поэтому β/D ≈ β/ω02 ≈ rа–1, и отношение (2.35) равно:
P(n+1) |
|
≈ |
e |
E |
|
≈ |
|
|
E |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P(n) |
m |
ω |
2 r |
|
E |
am |
|
||||||||
|
|
|
|||||||||||||
|
|
|
e |
0 |
|
a |
|
|
|
|
|
|
|||
Амплитуда напряженности светового вектора волны должна сравниваться с напряженностью внутриатомного поля, типичная величина которой, как уже отмечалось, составляет Еат = 1010…1011 В/м. Поэтому даже для предельных интенсивностей порядка 1014 Вт/м2, имеющих место в фокусе лазера с модулированной добротностью, нелинейность можно рассматривать как малое возмущение, поскольку даже в этом предельном случае отношение (2.35) равно:
50
